If the sides of a quadrilateral touch a circle, prove that the sum of a pair of opposite sides is equal to the sum of the other pair.
Matching exercise
Match the items on the right to the items on the left.
STEP 1
STEP 2
STEP 3
STEP 4
Given: the sides of a quadrilateral touch a circle
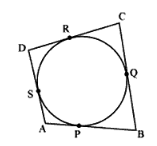
From the theoram which states that the lengths of the two tangents drawn from an external point to a circle are equal. From points A the tangents drawn are AP and AS, AP = AS .... (1)
From points B the tangents drawn are BP and BQ, BP = BQ ..... (2) From points D the tangents drawn are DR and DS, DR = DS ....(3) From points C the tangents drawn are CR and CQ, CR = CQ ..... (4)
Add 1,2,3 and 4 to get AP+BP+DR+CR = AS+BQ+DS+CQ(AP+BP)+(DR+CR )= (AS+DS)+ (BQ+CQ)AB+ DC = AD + BC Hence proved

