Circle

Circle:

A circle is a round shaped figure that has no corners or edges.  In geometry, a circle can be defined as a closed, two-dimensional curved shape.

Few things around us that are circular in shape are a car tire, a wall clock that tells time, and a lollipop. 

Center of a Circle

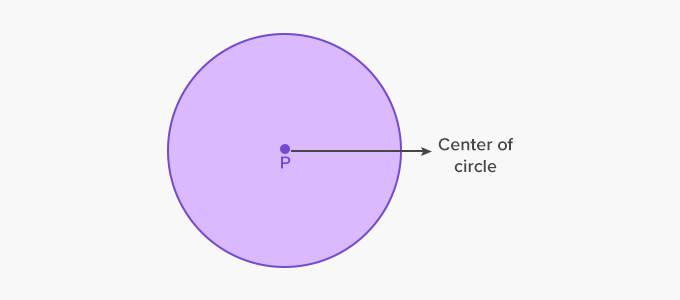
The center of a circle is the center point in a circle from which all the distances to the points on the circle are equal. This distance is called the radius of the circle.

Here, point P is the center of the circle.

Semicircle:

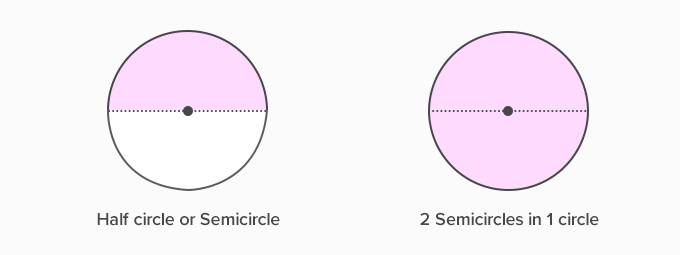
A semi-circle is half of a circle, formed by cutting a whole circle along a line segment passing through the center of the circle. This line segment is called the diameter of the circle.

Quarter Circle:

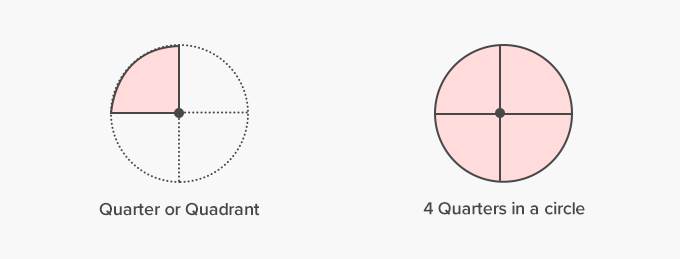
A quarter circle is a quarter of a circle, formed by splitting a circle into 4 equal parts or a semicircle into 2 equal parts. 

A quarter circle is also called a quadrant. 

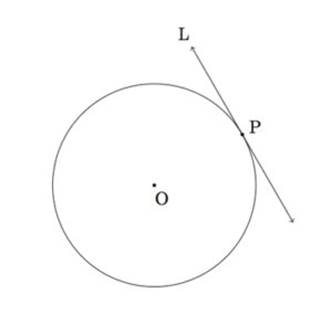
Tangent to a Circle

The line that joins two infinitely close points from a point on the circle is a Tangent. In other words, we can say that the lines that intersect the circles exactly in one single point are Tangents. Point of tangency is the point where the tangent touches the circle. At the point of tangency, a tangent is perpendicular to the radius. Several theorems are related to this because it plays a significant role in geometrical constructions and proofs. We will look at them one by one.

Tangents Formula

The formula for the tangent is given below. For the description of formula, please look at the following diagram.

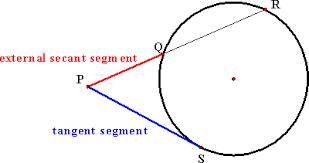
Here, we consider a circle where P is the exterior point. From that exterior point, the circle has the tangent at a points A and B. A straight line which cuts curve into two or more parts is known as a secant. So, here secant is PR is drawn and at Q, R intersects the circle as shown in the upper diagram. The formula for tangent-secant states that:

PR/PS = PS/PQ

PS² = PQ.PR

Properties of Tangents

Remember the following points about the properties of tangents-

The tangent line never crosses the circle, it just touches the circle.

At the point of tangency, it is perpendicular to the radius.

A chord and tangent form an angle and this angle is same as that of tangent inscribed on the opposite side of the chord.

From the same external point, the tangent segments to a circle are equal.

Theorems for Tangents to Circle

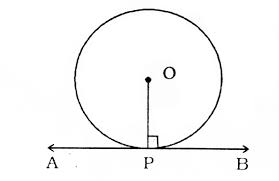
Theorem 1

A radius is obtained by joining the centre and the point of tangency. The tangent at a point on a circle is at right angles to this radius. Just follow this below diagram: Here AB⊥OP

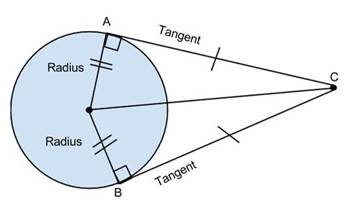
Theorem 2

This theorem states that if from one external point, two tangents are drawn to a circle then they have equal tangent segments. Tangent segment means line joining to the external point and the point of tangency. Consider the following diagram: Here, AC=BC.

These are some of the basic theorems on tangents to a circle. In the next section, we will look at some of the basic properties of tangents.

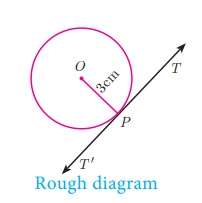
Construction of a tangent to a circle (Using the centre)

Draw a circle of radius 3 cm. Take a point P on this circle and draw a tangent at P.

Solution 

Given, radius r = 3 cm

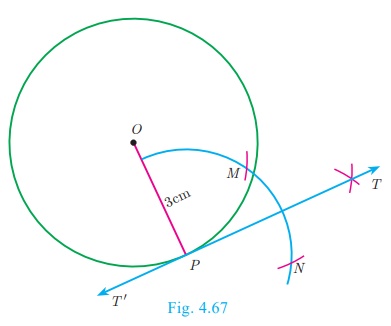
Construction

Step 1: Draw a circle with centre at O of radius 3 cm.

Step 2: Take a point P on the circle. Join OP.

Step 3: Draw  perpendicular  line TT’  to  OP which  passes through P.

Step 4:  TT ‘ is the required tangent.

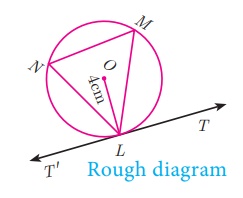
Construct of a tangent to a circle (Using alternate segment theorem)

Draw a circle of radius 4 cm. At a point L on it draw a tangent to the circle using the alternate segment.

Solution

Given, radius=4 cm

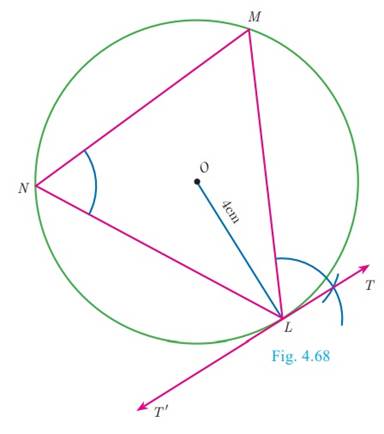
Construction

Step 1 : With O as the centre, draw a circle of radius 4 cm.

Step 2: Take a point L on the circle. Through L draw any chord LM.

Step 3: Take a point M distinct from L and N on the circle, so that L, M and N are  in anti-clockwise direction. Join LN and NM.

Step 4: Through L draw a tangent TT ’ such that ∠TLM = ∠MNL.

Step 5: TT ‘ is the required tangent.

Construction of pair of tangents to a circle from an external point P.

Draw a circle of diameter 6 cm from a point P, which is 8 cm away from its centre. Draw the two tangents PA and PB to the circle and measure their lengths.

Solution

Given, diameter (d) = 6 cm, we find radius (r) = 6/2 = 3 cm

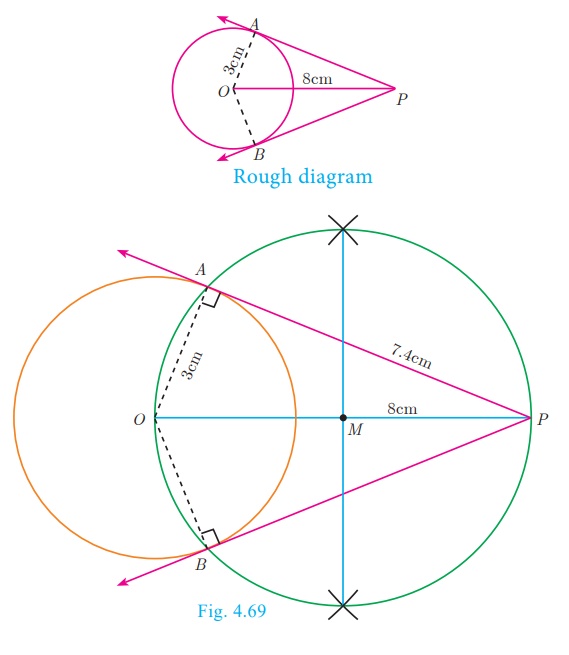
Construction

Step 1: With centre at O, draw a circle of radius 3 cm.

Step 2: Draw a line OP of length 8 cm.

Step 3: Draw a perpendicular bisector of OP, which cuts OP at M.

Step 4: With M as centre and MO as radius, draw a circle which cuts previous circle at A and B.

Step5: Join AP and BP. AP and BP are the required tangents. Thus length of the tangents are PA = PB = 7.4 cm.

Verification :

In the right angle triangle OAP , PA2 = OP2 −OA2 = 64 – 9 = 55

PA = √55 = 7 4. cm (approximately) .

Prove that the length of tangents drawn from an external point to a circle are equal.

Given:

A circle with centre O; PA and PB are two tangents to the circle drawn from an external point P.

To prove:

PA = PB

Construction:

Join OA, OB, and OP.

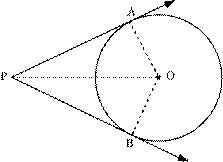
It is known that a tangent at any point of a circle is perpendicular to the radius through the point of contact.

 OA  PA and OB  PB ... (1)

In OPA and OPB:

OAP = OBP (Using (1))

OA = OB (Radii of the same circle)

OP = OP (Common side)

Therefore, OPA  OPB (RHS congruency criterion)

PA = PB

(Corresponding parts of congruent triangles are equal)

Thus, it is proved that the lengths of the two tangents drawn from an external point to a circle are equal.

2. Prove that in two concentric circles the chord of the larger circle which touches the smaller circle is bisected at the point of contact

solution:

Let there is a circle having center O

Let AB is the tangent to the smaller circle and chord to the larger circle.

Let P is the point of contact.

Now, draw a perpendicular OP to AB

Now, since AB is the tangent to the smaller circle,

So, ∠OPA = 90

Now, AB is the chord of the larger circle and OP is perpendicular to AB.

Since the perpendicular drawn from the center of the circle to the chord bisect it.

So, AP = PB

Hence, in two concentric circles, the chord of the larger circle which touches the smaller circle is bisected at the point of contact.

3. Two tangents TP and TQ are drawn to a circle with center O from an external point T. Prove that angle PTQ = 2 OPQ.

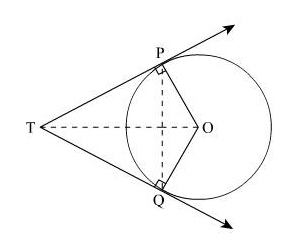
We know that, the lengths of tangents drawn from an external point to a circle are equal.

∴ TP = TQ

In ΔTPQ,

TP = TQ

⇒ ∠TQP = ∠TPQ ...(1) (In a triangle, equal sides have equal angles opposite to them)

∠TQP + ∠TPQ + ∠PTQ = 180º (Angle sum property)

∴ 2 ∠TPQ + ∠PTQ = 180º (Using(1))

⇒ ∠PTQ = 180º – 2 ∠TPQ ...(1)

We know that, a tangent to a circle is perpendicular to the radius through the point of contact.

OP ⊥ PT,

∴ ∠OPT = 90º

⇒ ∠OPQ + ∠TPQ = 90º

⇒ ∠OPQ = 90º – ∠TPQ

⇒ 2∠OPQ = 2(90º – ∠TPQ) = 180º – 2 ∠TPQ ...(2)

From (1) and (2), we get

∠PTQ = 2∠OPQ