Introduction
Area of a Circle:
Any geometrical shape has its own area. This area is the
region occupied the shape in a two-dimensional plane. Now we will learn about
the area of the circle. So the area covered by one complete cycle of the radius
of the circle on a two-dimensional plane is the area of that circle
Area of a circle is πr2, where π=22/7
or ≈3.14 (can be used interchangeably for problem-solving
purposes) and r is the radius of the circle.
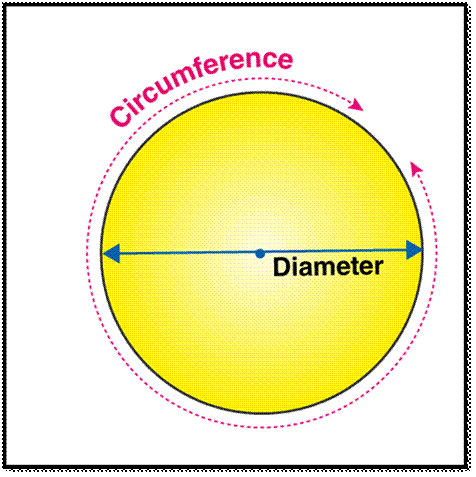
π is the ratio of the circumference of a
circle to its diameter.
Area of a Circle Formula:
Let us take a circle with radius r.
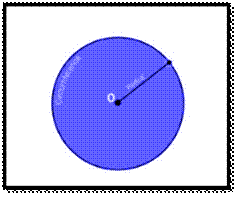
where radius r from the
centre ‘o’ to the boundary of the circle. Then the area for this circle, A, is
equal to the product of pi and square of the radius. It is given by;
Area of a Circle, A = πr2 square
units
Perimeter and Area of a
Circle — A Review :
Circumference of the circle or perimeter of the
circle is the measurement of the boundary across any
two-dimensional circular shape including circle. Whereas the area of circle, defines the region occupied by it. If we open a
circle and make a straight line out of it, then its length is the
circumference. It is usually measured in unit cm or unit m..
Circumference of a Circle Formula :
The Circumference (or) perimeter of a circle = 2πR
where,
R is the radius of the circle
π is the mathematical constant with an
approximate (up to two decimal points) value of 3.14
Again,
Pi (π) is a special mathematical
constant, it is the ratio of circumference to diameter of any circle.
where C = π D
C is the circumference of the circle
D is the diameter of the circle
For example:
If Radius Of The Circle Is 4cm Then
Find Its Circumference.
Solution:
Given:
Radius = 4cm
Circumference = 2πr
= 2 x 3.14 x 4
= 25.12 cm
Circumference of Circle:
The circumference is the distance
around a circle or any curved geometrical shape. It is the one-dimensional
linear measurement of the boundary across any two-dimensional circular surface.
It follows the same principle behind finding the perimeter of any polygon which
is why calculating the circumference of a circle which is also known as
the perimeter of a circle.
A circle is defined as a shape with
all the points are equidistant from a point at the centre. The circle depicted
below has its centre lies at point A.
The value
of pi is approximately 3.1415926535897… and we use a Greek
letter π (pronounced as Pi) to describe this number. The value π is a
non-terminating value.
Example 1 :
The cost of fencing a circular field at the rate of ` 24 per metre is` 5280. The field is to be ploughed at the rate of ` 0.50 per m2. Find the
cost of ploughing the field (Take π =22/7 ).
Solution
:
For Rs. 24 , the length of fencing =1m
For Rs. 5280, the length of fencing = ![]()
![]() 5280 = 220 metres.
5280 = 220 metres.
Circumference of the field = 220 m
2pr =220
2x ![]()
![]() r =220
r =220 ![]()
Area of the field = ![]() r2 =
r2 = ![]() (35)2 =1225
(35)2 =1225![]() m2
m2
Cost of ploughing = Rs. 0.50 per m2
Total cost of ploughing the field = Rs. 1225 ![]() x 0.50
x 0.50
= Rs. ![]()
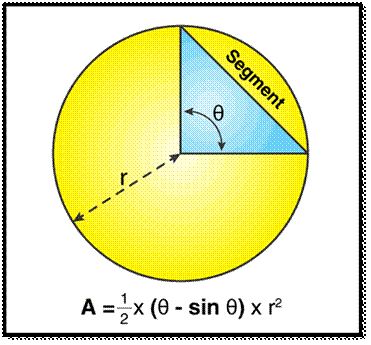
Areas of Sector and
Segment of a Circle :
Definition :
A segment of a circle can be defined
as a region bounded by a chord and a corresponding arc lying between the
chord’s endpoints. So, it can be said that a circular segment is a region of a
circle which is created by breaking apart from the rest of the circle through a
secant or a chord.
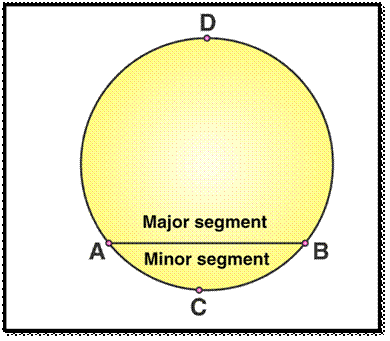
Types of Segments in a Circle :
There are two
classifications of segments in a circle namely the major segment and the minor segment. The segment having
larger area is known as the major segment and the segment having a smaller area
is known as minor segment.
Area of a Segment of a Circle Formula :
The formula to find segment area can
be either in terms of radians or in terms of degree.
Example 2 :
Find the area of the sector of a circle with radius 4 cm and of
angle 30°. Also, find the area of the corresponding major sector (Use π = 3.14).
Solution
:
Area
Of Sector =Θ
/ 360⋅Πr2
=Θ360⋅πr2
=30/360⋅3.14⋅42
=1 / 2–√⋅3.14⋅16
=12.56
/ 3
=4.186cm2
now, area of major sector =π⋅r2−4.186cm2
=3.14⋅16−4.186
=50.24−4.186
=46.054cm2
Area of combinations of plane figures :
A
collection of points that are on a plane is known as a plane figure.
Calculate the area
of the figure, which has a non-standard form is involving basic geometric
figures such as circles, squares, triangles, rectangles etc.

Area of the figure
= Area of the rectangle + 2 x Area of semi circles.
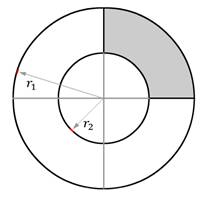
Area of the required region = ( πr12 – πr22).
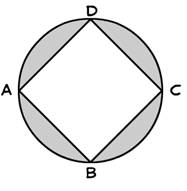
Area of the required region = πr2 – a2 .
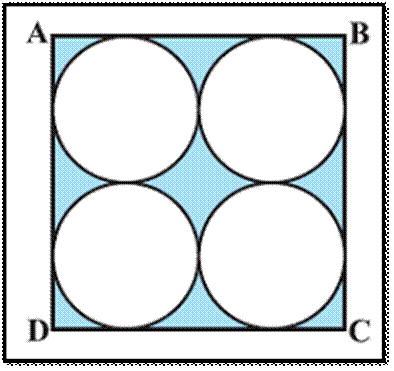
Example 5 :
Find
the area of the shaded region where ABCD is a square of side 14cm
. ( four equal circle inside the square)
Area of Square ABCD
14 * 14 cm2
= 196 cm2
Diameter of each Circle
14 / 2 cm
= 7 cm
Radius of each Circle
= 7 /2 cm
Area of one Circle
= πr2
= 22 / 7 * 7 / 2 * 7 / 2
= 154 / 4
= 77 / 2 cm2
Area of Four Circle
4* 77 / 2cm2
= 154 cm2
Area of Shaded Region
Area of Shaded Region = Area of Square ABCD -
Area of four Circles
= ( 196 - 154 ) cm2
= 42 cm2
Example
:6
Find
the area of the shaded design in Fig. 12.17, where ABCD is a square of side 10
cm and semicircles are drawn with each side of the square as diameter. (Use
π = 3.14)
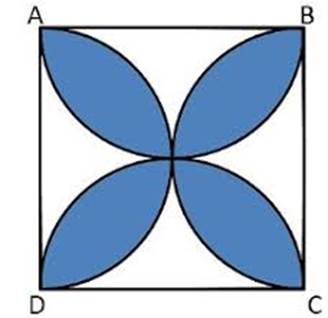
Let Unshaded
regions be 1, 2, 3 and 4
Area
of 1 + Area of 3= Area of ABCD – Areas of two semicircles of each of radius 5
cm
Area of 1 and 3 = ( 10 * 10 - 2 * 1/2 * 3.14 * 5 *5) [Area of semi
circle = 1/2 pie r²]
= (100 -
3.14 * 25)
= (100 -
78.5)
=21.5 cm²
So,
Even the
Area of 2 and 4 is equal to 21.5cm²
So,
Area of
shaded region = Area of ABCD - Area 0f( 1+2+3+4)
=
100 - (21.5 + 21.5)
=
100 - 43
Area of
shaded region = 57cm²