Surface Area and Volume
INTRODUCTION:
Surface area and volume are calculated for any three-dimensional
geometrical shape. The surface area of any given object is the area covered or
region occupied by the surface of the object. Whereas volume is the amount of
space available in an object. We have learned so far in geometry about
different shapes and sizes such as sphere, cube, cuboid, cone, cylinder, etc.
Each shape has its surface area as well as volume. But in the case of
two-dimensional figures like square, circle, rectangle, triangle, etc.
AREA:
The space occupied
by a two-dimensional flat surface. It is measured in square units.
Generally, Area
can be of two types
![]() Total Surface Area
Total Surface Area
![]() Curved Surface
Area
Curved Surface
Area
TOTAL SURFACE AREA :
Total surface area
refers to the area including the base(s) and the curved part.
CURVED SURFACE AREA (LATERAL SURFACE
AREA) :
Refers to the area
of only the curved part excluding its base(s).
VOLUME:
The amount of
space, measured in cubic units, that an object or substance occupies. Some
shapes are two-dimensional, so it doesn’t have volumes.
Example,
Volume of Circle cannot be
found, though Volume of the sphere can be. It is so because a sphere is a
three-dimensional shape.
Table for Calculating Surface Area And Volume For
The Basic Geometrical Figures
|
Name |
Perimeter |
Total Surface
Area |
Curved Surface
Area |
Volume |
Figure |
|
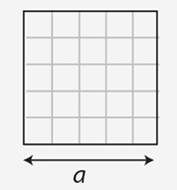
Square |
4a |
a2 |
—- |
—- |
|
|
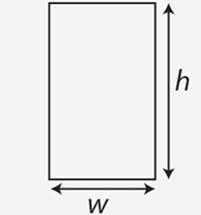
Rectangle |
2(w+h) |
w.h |
—- |
—- |
|
|
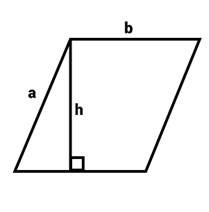
Parallelogram |
2(a+b) |
b.h |
—- |
—- |
|
|
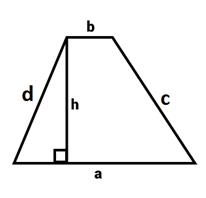
Trapezoid |
a+b+c+d |
1/2(a+b).h |
—- |
—- |
|
|
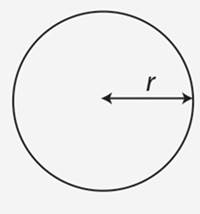
Circle |
2 π r |
π r2 |
—- |
—- |
|
|
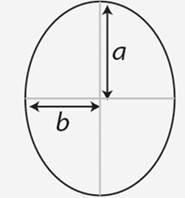
Ellipse |
2π√(a2 +
b2)/2 |
π a.b |
—- |
—- |
|
|
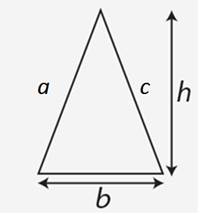
Triangle |
a+b+c |
1/2 * b * h |
—- |
—- |
|
|
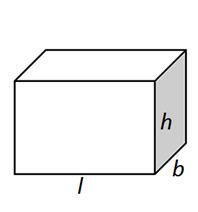
Cuboid |
4(l+b+h) |
2(lb+bh+hl) |
2h(l+b) |
l * b * h |
|
|
Cube |
6a |
6a2 |
4a2 |
a3 |
|
|
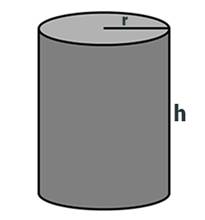
Cylinder |
—- |
2
π r(r+h) |
2πrh |
π r2 h |
|
|
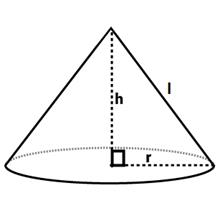
Cone |
—- |
π r(r+l) |
π r l |
1/3π r2 h |
|
|
Sphere |
—- |
4 π r2 |
4π r2 |
4/3π r3 |
|
|
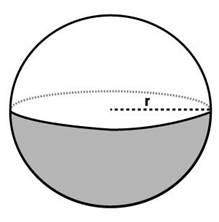
Hemisphere |
—- |
3 π r2 |
2 π r2 |
2/3π r3 |
|
SURFACE AREA
OF A COMBINATION OF SOLIDS:
Solid shapes are three-dimensional structures of otherwise planar shapes.
A square becomes a cube, a rectangle is a cuboid and a triangle becomes a cone when changed to a 3-d structure. For planar
shapes, our measurement is limited to just the area of that shape.
But when we need to measure 3-d shapes we intend to scale their volume,
surface area or curved surface area. Solid shapes as already said are 3-d
counterparts of their planar shape.
A combination of a solid is that figure which is formed by
combining two or more different solids. Two cubes may combine to
form a cuboid, while a cone over a cylinder might fuse to form a
tent.

EXAMPLES OF COMBINATIONS OF SOLIDS :
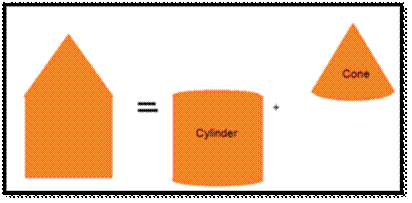
A CIRCUS TENT OR A HUT :
A circus tent is a combination of a cylinder and a cone. Some circus
tents also constitute a cuboid and a cone. A hut is a kutcha house and has
a tent-like structure.
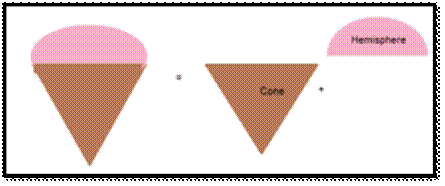
AN ICE CREAM CONE :
An ice cream cone is a combination of a cone and a hemisphere.
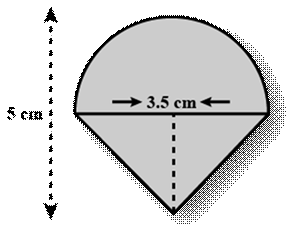
EXAMPLE
1:
Rasheed got a playing
top (lattu) as his birthday present, which surprisingly had no colour on it. He
wanted to colour it with his crayons. The top is shaped like a cone surmounted
by a hemisphere. The entire top is 5cm in
height and the diameter of the top is 3.5cm.
Find the area he has to colour (Take π=22/7)
ANSWER :
Radius of hemispherical portion of the lattur
= 3.5 / 2 = 7/4cm.
Radius of the conical portion r=
3.5 / 2 = 7/ 4 cm
Height of the conical portion h=(5−
3.5 / 2 )= 13 / 4 cm
Slant height of the conical part l=![]()
l= ![]() =
= ![]() 3.69cm≈3.7cm
3.69cm≈3.7cm
Total surface area of the top will be,
2πr2 +πrl=πr(2r+l)=22
/ 7 × 7 / 4 (2 × 7 / 4+3.7)=39.6cm2
EXAMPLE 2:
A decorative block shown
in figure, is made of two solids- a cube and a hemisphere. The base of the
block is a cube with edge 5cm, and the
hemisphere fixed on the top has a diameter 4.2cm.
Find the total surface area of the block (Take π=22/7)
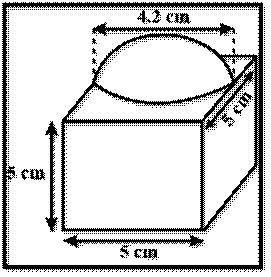
ANSWER:
Edge of cube= 5 cm
Diameter of hemisphere= 4.2 cm
Clearly
Surface area of decorative block
= total surface area of the cube - base area of hemisphere + curved
surface area of hemisphere
=(6×(edge)2−πr2+2πr2)cm2
=(25×6+πr2)cm2
={150+722×(2.1)2}cm2
=163.86cm2
VOLUME OF A
COMBINATION OF SOLIDS :
A
solid which is bounded by six rectangular faces is known as cuboids and if the
length, breadth and height of the cuboids are equal, then it is a cube.
8
vertices, 6 faces and 12 edges are there in both cube as well as cuboids. Base
of the cuboids is any face of the cuboids.
For
a cuboids which has length (l), breadth (b) and height (h) has:
![]() Volume
= l×b×h
Volume
= l×b×h
![]() Total
surface area = 2(lb+bh+lh)
Total
surface area = 2(lb+bh+lh)
For
a cube with length x,
![]() Volume
= x3 (because l = b = h = x)
Volume
= x3 (because l = b = h = x)
![]() Total
surface area = 6x2
Total
surface area = 6x2
EXAMPLE !:
Shanta runs an industry in
a shed which is in the shape of a cuboid surmounted by a half cylinder. If the
base of the shed is of dimensions7 m*15 m and the height of the cuboidal
portion is 8 m, find the volume of the air the shed can hold. 2. The inner diameter
of a cylindrical glass is 5 cm, but the bottom of the glass has a hemispherical
raised portion reducing the capacity of the glass. If the height of the glass
is 10 cm, find the apparent and actual capacity of the glass.
ANSWER:
Solution: Volume of Cuboid = lbh
→ 7 m × 15 m × 8 m
→ 840 m³
Let's focus now on half
cylinder, 7 m is diameter and 15 m.
Volume of cylinder =
πr²h
→ 22/7 × (7/2)² × 15
m³
→ 22/7 × 7/2 × 7/2 ×
15 m³
→ 22 × 1/2 × 7/2 × 15
m³
→ 577.5 m³
But since cylindrical shed
is half hence,
→ 577.5 m³/2 = 288.75
m³
Total Volume = 840 m³ +
288.75 m³
→ 1128.75 m³
Volume occupied = Volume of
machinery + Volume of 20 workers
→ 300 m³ + 20(0.08)m³
→ 301.6 m³
Remaining volume of air =
1128.75 m³ - 301.6 m³
→ 827.15 m³
Answer: 827.15 m³
EXAMPLE: 2
A juice seller was serving
his customers using glass. The inner diameter of the cylindrical glass
was 5 cm , but the bottom of the glass had a
hemispherical raised portion which reduced the capacity of the glass. If the
height of the glass was 10 cm, find what the apparent capacity of the glass was
and what the actual capacity was (Use π=3.14)
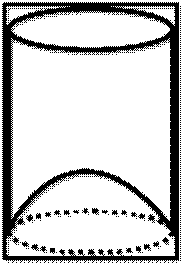
ANSWER
REF.Image.
Actual capacity of Glass= Volume of
cylinder - Volume of hemisphere
⇒ volume of cylinder=πr2h
where r=D / 2=5 / 2cm;
h=10cm;D=3.14
⇒3.14×(5 / 2)2×10
⇒3.14×6.25×10
⇒196.25cm3
Volume of Hemisphere ⇒2 / 3πr3
(r=5 / 2)
⇒2 / 3×3.14×(5 / 2)3
⇒2 / 3×3.14×15.625
⇒32.7cm3
∴ Actual
capacity 196.25−32.7=163.55cm3
EXAMPLE 3
A solid toy is in the form of a hemisphere surmounted by
a right circular cone. Height of the cone is 2cm and
the diameter of the base is 4cm. If a right
circular cylinder circumscribes the toy, find how much more space it will
cover.
ANSWER
Volume of toy = Vol. of cone +
Vol.of hemisphere
=1 / 3 πr2H
+ 2 / 3πr3=1 / 3πr2[H+2r]h
=1 / 3 × 22 /
7×2×2[2+2×2]
=1 / 3×22 / 7 ×4×62
=25.12cm3
Volume of cylinder =πr2h
=22 /
7×2×2[2+2]
=22 /
7×16
=50.24cm3
Difference in
volume =50.24−25.12=25.12cm3
Hence, cylinder cover 25.12cm 3more space.
Conversion
From One Shape to Another
Each
and every solid that exists occupies some volume. When you convert one solid
shape to another, its volume remains the same, no matter how different the new
shape is. In fact, if you melt one big cylindrical candle to 5 small
cylindrical candles, the sum of the volumes of the smaller candles is equal to
the volume of the bigger candle.
Examples
Selvi's house has an
overhead tank in the shape of a cylinder. This is filled by pumping water from
a sump (underground tank). Which is in the shape of a cuboid. The sump has
dimensions 1.57m×1.44m×0.95m.
The overhead tank has its radius of 60cm and
its height is 95cm. Find the height of the
water, left in the sump after the overhead tank has been completely filled with
water from a sump which had been full. Compare the capacity of the tank with
that of the sump (Use π=22/7)
ANSWER
Clearly the volume of the water in the
overhead tank is equal to the volume of the water removed from the sump.
Now Volume of water in the overhead tank =3.14×0.6×0.6×0.95m3=3.14×0.36×0.95m3
Volume of water in the sump when it is full of water =1.57 × 1.44 × 0.95m3=1.57×4
× 0.36 × 0.95m3 =2 × 3.14× 0.36 × 0.95m3
Volume of water left in the sump after filling the tank
(2×3.14×0.36×0.95−3.15×0.36×0.95)m3=3.14×0.36×0.95m3
Area of the base of the sump =1.57×1.44m3=1.57×4×0.36m3=2×3.14×0.36m3
Height of the water in the sump = ![]() m=0.95
/ 2 =47.5cm
m=0.95
/ 2 =47.5cm
Now ![]() =
=![]() =
=![]()
EXAMPLE :
A copper rod of diameter 1 cm and length 8 cm is drawn
into a wire of length 18 m of uniform thickness. Find the thickness of the
wire.
Sol:
The volume of the rod = π×(![]() )2×8=2π cm3
)2×8=2π cm3
The length of the new wire of the same
volume = 18 m = 1800 cm
If r is the radius ( in cm ) of
cross-section of the wire, its voume = π×r2×1800 cm3
Therefore,
π×r2×1800=2π
r2=![]()
r= ![]()
So, the diameter of the cross section, i.e.,
the thickness of the wire is ![]() cm, i.e., 0.67 mm (approx.)
cm, i.e., 0.67 mm (approx.)
Frustum of cone
In the combination
of solids, we added the volumes of two adjoining shapes which gave us the total
volume of any structure. But for frustum of the cone as we are slicing the
smaller end of the cone as shown in the figure, hence we need to subtract the
volume of the sliced part.
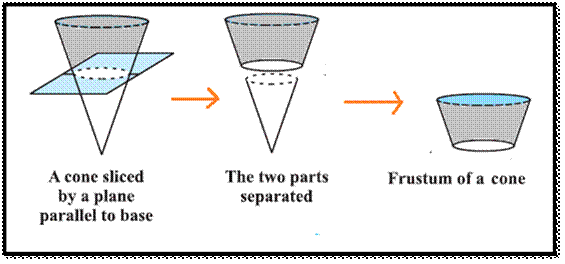
The Volume of the Frustum of a
Cone
The frustum as said
earlier is the sliced part of a cone, therefore for calculating the volume, we find
the difference of volumes of two right circular cones.
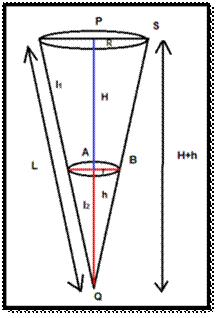
From the figure, we
have, the total height H’ = H+h and the total slant height L =l1 +l2.
The radius of the cone = R and the radius of the sliced cone = r. Now the volume of the total cone =
1/3 π R2 H’ = 1/3 π R2 (H+h)
The volume of the Tip
cone = 1/3 πr2h. For finding the volume of the
frustum we calculate the difference between the two right circular cones, this
gives us
= 1/3 π
R2 H’ -1/3 πr2h
= 1/3π R2 (H+h) -1/3 πr2h
=1/3 π [ R2 (H+h)-r2 h ]
Now on seeing the whole
cone with the sliced cone, we come to know that the right angle of the whole cone Δ QPS is similar to the sliced
cone Δ QAB. This gives us, R/ r = H+h / h ⇒ H+h = Rh/r. Substituting the value of H+h in the formula for
the volume of frustum we get,
=1/3 π [ R2 (Rh/r)-r2 h ]
=1/3 π [R3h/r-r2 h]
=1/3 π h (R3/r-r2 ) =1/3 π h (R3-r3 /
r)
The Volume of Frustum
of Cone = 1/3 π h [(R3-r3)/ r]
EXAMPLE 1:
Hanumappa and his wife
Gangamma are busy making jaggery out of sugarcane juice. They have processed
the sugarcane juice to make the molasses,which is poured into moulds in the
shape of a frustum ol a cone having the diameters of its two circular faces as
30 cm and 35 cm and the vertical height of the mould is14 cm (see Fig. 13.22).
If each cm of molasses has mass about 1.2 g, find the mass of the molasses that
can Fig. 13 be poured into each mould.
ANSWER:
It is given that,
The mould is in the shape of a frustum of a cone whose dimensions
are:
The lower base diameter, d1 = 30 cm
∴ the radius, r1 = 30/2 = 15 cm
The upper base diameter, d2 = 35 cm
∴ the radius, r2 = 35/2 = 17.5 cm
The vertical height, h = 14 cm
We know that,
The quantity/volume of the molasses that can be poured into the
frustum will be given by,
= The volume of the frustum
= 1/3 × π × h [r1² + r2²+ (r1×r2)]
= 1/3 × (22/7) × 14 × [(15)² + (17.5)² + (15 × 17.5)]
= (44/3) × [225 + 306.25 + 262.5]
= (44/3) × 793.75
= 11641.67 cm³
It is given that: 1 cm³ of molasses = 1.2 g
Thus,
The mass of the molasses that can be poured into each mould is,
= 11641.67 × 1 2
= 13970.004 g
[∵ 1g = 1/1000 kg]
= 13970.004/1000
= 13.97 kg
≈ 14 kg (approx)
EXAMPLE:
An open metal bucket is in shape of a
frustum mounted on a cylindrical base made of same metallic sheet the dia of
two circular ends of bucket are 45 and 25 cm the total height of bucket is 40
cm and base of cylinder is 6cm find area of metallic sheet
Solution :-
Area of metallic sheet used = CSA of Frustum + CSA
of Cylinder + CSA of Base
Diameter of the bigger circular end = 45 cm
Radius = 45/2 = 22.5 cm
Diameter of the smaller circular end = 25 cm
Radius = 25/2 = 12.5 cm
Height of the frustum = Total height of the bucket
- Height of the circular base
⇒ 40
- 6 = 34 cm
Slant Height = l √h² + (r1² - r2²)²
⇒ √34²
+ (22.5 - 12.5)²
⇒
√1156 + (10)²
⇒ √1156
+ 100
⇒ √1256
⇒
Slant Height = 35.44 cm
CSA of Frustum = π(r1 + r2)l
⇒
22/7*(22.5 + 12.5)*35.44
⇒
22/7*35*35.44
= 3898.4 cm²
Base is a circular part with radius 25/2 = 12.5 cm
Area of circular base = πr²
⇒
22/7*12.5*12.5
491.07 cm²
CSA of Cylinder = 2πrh
⇒
2*22/7*12.5*6
⇒
471.428
Area of metallic sheet used = 3898.4 cm² + 491.07
cm² + 471.428
= 4860.898 cm²