Statistics
INTRODUCTION:
Mathematical statistics is the application of Mathematics to
Statistics, which was originally conceived as the science of the state — the
collection and analysis of facts about a country:
![]() its economy, and, military, population,
and so forth.
its economy, and, military, population,
and so forth.
Mathematical techniques used for this include mathematical
analysis, linear algebra, stochastic analysis, differential equation and
measure-theoretic probability theory.
SCOPE
Statistics is used in many sectors such as psychology, geology,
sociology, weather forecasting, probability and much more. The goal of
statistics is to gain understanding from data it focuses on applications and
hence, it is distinctively considered as a Mathematical science.
Methods
The methods involve collecting, summarizing, analyzing, and
interpreting variable numerical data. Here are some of the methods provided
below.
![]() Data collection
Data collection
![]() Data summarization
Data summarization
![]() Statistical analysis
Statistical analysis
Data
Data is a collection of facts, such as numbers, words,
measurements, observations etc.
Types of Data-
1.
Qualitative data- it is descriptive data.
·
Example- She
can run fast, He is thin.
Quantitative data- it is numerical information.
·
Example- An
Octopus is an Eight legged creature.
Types of quantitative data :
1.
Discrete data- has a particular
fixed value. It can be counted
2.
Continuous data- is not
fixed but has a range of data. It can be measured.
Representation of Data-
|
|
Bar Graph |
|
|
Pie Chart |
|
|
Line graph |
|
|
Pictograph |
|
|
Histogram |
|
|
Frequency
Distribution |
The mean (or average) of
observations, is the sum of the values of all the observations divided by the
total number of observations.
If x1, x2,.
. ., xn are observations with respective frequencies
f1, f2, . . ., fn,
then this means observation x1
occurs f1 times, x2 occurs f2 times, and so on.
Now, the sum of the values of all the observations = f1x1 + f2x2
+ . . . + fnxn, and sum of the number of observations
= f1 + f2 + . . . + fn.
So, the mean x of the data is given by
x=
f1x1+f2x+…fnxn / f1+f2+…fn
EXAMPLE 1:
The marks obtained by 30 students of Class X of a certain school
in a Mathematics paper consisting of 100 marks are presented in table below.
Find the mean of the marks obtained by the students.
|
Marks obtained xi |
10 |
20 |
36 |
40 |
50 |
56 |
60 |
70 |
72 |
80 |
88 |
92 |
95 |
|
Number of students fi |
1 |
1 |
3 |
4 |
3 |
2 |
4 |
4 |
1 |
1 |
2 |
3 |
1 |
Solution:
To find the mean marks, we require the product of each xi with
the corresponding frequency fi.
|
Marks obtained (xi) |
Number of students (fi) |
fixi |
|
10 |
1 |
10 |
|
20 |
1 |
20 |
|
36 |
3 |
108 |
|
40 |
4 |
160 |
|
50 |
3 |
150 |
|
56 |
2 |
112 |
|
60 |
4 |
240 |
|
70 |
4 |
280 |
|
72 |
1 |
72 |
|
80 |
1 |
80 |
|
88 |
2 |
176 |
|
92 |
3 |
276 |
|
95 |
1 |
95 |
|
Total |
Σ fi = 30 |
Σ fixi = 1779 |
x=Σfixi / Σfix=Σfixi / Σfi
=1779 / 30=59.3
DIRECT METHOD OF FINDING MEAN:
|
lass Intervals |
10-25 |
25-40 |
40-55 |
55-70 |
70-85 |
85-100 |
|
Number of students |
2 |
3 |
7 |
6 |
6 |
6 |
Now, for each class-interval, we require a point which would
serve as the representative of the whole class. It is assumed that the
frequency of each class-interval is centered around its mid-point. So the mid-point
(or class mark) of each class can be chosen to represent the observations
falling in the class.
Class Mark = (Upper class limit + Lower class limit)/2
|
Class Interval |
Number of students (fi) |
Class Mark (xi) |
fixi |
|
10-25 |
2 |
17.5 |
35 |
|
25-40 |
3 |
32.5 |
97.5 |
|
40-55 |
7 |
47.5 |
332.5 |
|
55-70 |
6 |
62.5 |
375.0 |
|
70-85 |
6 |
77.5 |
465.0 |
|
85-100 |
6 |
92.5 |
555.0 |
|
Total |
Σ fi = 30 |
&Sigma fixi = 1860 |
x=Σfixi / Σfi=Σfi
=1860 / 30=62
This method of finding the mean is known as the Direct Method.
Here, 59.3 is the exact mean, while 62 is an approximate mean.
ASSUMED MEAN METHOD:
Sometimes when the numerical
values of xi and fi are large, finding the product of xi and fi becomes tedious
and time consuming. So, for such situations, let us think of a method of
reducing these calculations.
|
Class
Interval |
Number
of Students (fi) |
Class Mark
(xi) |
di = xi
- a |
fidi |
|
10-25 |
2 |
17.5 |
-30 |
-60 |
|
25-40 |
3 |
32.5 |
-15 |
-45 |
|
40-55 |
7 |
47.5 |
0 |
0 |
|
55-70 |
6 |
62.5 |
15 |
90 |
|
70-85 |
6 |
77.5 |
30 |
180 |
|
85-100 |
6 |
92.5 |
45 |
270 |
|
Total |
Sum fi = 30 |
Sum fidi = 435 |
So, the mean of deviations:
d=Σfidi / Σfi=435 /
30=14.5
Since d is obtained by subtracting a from
xi so x can be obtained as follows:
x=d̅+a=14.5+47.5=62.
MODE OF GROUPED DATA:
Statistics deals with the
presentation, collection and analysis of data and information for a particular
purpose. To represent this data we use tables, graphs, pie-charts, bar graphs, pictorial
representation and so on. After the proper organization of the data, it must be
further analyzed to infer some useful information from it.
For this purpose, frequently in
statistics, we tend to represent a set of data by a representative value which
would roughly define the entire collection of data. This representative value
is known as the measure of central tendency. By the name itself, it suggests
that it is a value around which the data is centred.
These measures of central tendency allow us to create a statistical summary of
the vast organized data. One such method of measure of central tendency is the
mode of data.
Example:
The following table represents the number of wickets taken by a
bowler in 10 matches. Find the mode of the given set of data.

It can be seen that 2 wickets were taken by the bowler
frequently in different matches. Hence, the mode of the given data is 2.
EXAMPLE 1
The wickets taken by a bowler in 10 cricket
matches are as follow: 2,6,4,5,0,2,1,3,2,3 Find the
mode of the data
ANSWER:
First arrange them in ascending
order then the no. which is repeated many times or seen many times is the mode
of the data
Here,
A.O:-
0,1,2,2,2,3,3,4,5,6
we can
see that 2 is seen more times(3times),
so 2
is the mode of the data
EXAMPLE 2:
A survey conducted on 20 households
in a locality by a group of students resulted in the following frequency table
for the number of family members in a household.
|
Family size |
1-3 |
3-5 |
5-7 |
7-9 |
9-11 |
|
Number of families |
7 |
8 |
2 |
2 |
1 |
ANSWER
⇒
Here,
modal class =3−5
⇒ l=3,f0=7,f1=8,f2=2 and h=2
⇒ Mode=l+ ![]() ×h
×h
=3+ ![]() ×2
×2
=3+![]() ×2
×2
=3+0.286
∴ Mode =3.286
MEDIAN OF GROUPED DATA:
The median of a set of data is the
middlemost number in the set. The median is also the number that is halfway
into the set. To find the median, the data should first be arranged in order
from least to greatest. A median is a number that is separated by the higher
half of a data sample, a population or a probability distribution,
from the lower half.
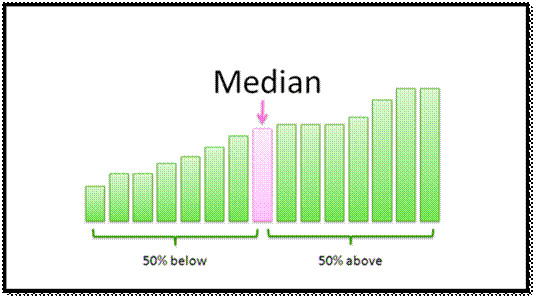
For example,
The median of 3, 3, 5, 9, 11
is 5. If there is an even number of observations, then there is no single
middle value; the median is then usually defined to be the mean of the two
middle values: so the median of 3, 5, 7, 9 is (5+7)/2 = 6.
Median Formula
The formula to calculate the median of the data set is given as
follows:
If the total number of observation given is odd, then the
formula to calculate the median is:
Median = {(n+1)/2}thterm
If the total number of observation is even, then the median
formula is:
Median =
[(n/2)th term + {(n/2)+1}th]/2
To find the median, place all the numbers in value order and
find the middle.
Example 1:
Find the Median of 14, 63 and 55
Solution:
Put them in order: 14, 55, 63
The middle is 55, so the median is 55.
Example 2:
Find the median of the following:
4, 17, 77, 25, 22, 23, 92, 82, 40, 23, 14, 12, 67, 23, 29
Solution:
When we put those numbers in the order we have:
4, 12, 14, 17, 22, 23, 23, 24, 25, 29, 40, 67, 77, 82, 92,
There are fifteen numbers. Our middle is the eighth number:
The median value of this set of numbers is 24.
Example 3:
Rahul’s family drove through 7 states
on summer vacation. The prices of Gasoline differ from state to state.
Calculate the median of gasoline cost.
1.79, 1.61, 2.09, 1.84, 1.96, 2.11, 1.75
Solution:
By organizing the data from smallest
to greatest, we get:
1.61, 1.75, 1.79, 1.84 , 1.96, 2.09, 2.11
Hence, the gasoline cost is 1.84. There are three states with
greater gasoline costs and 3 with smaller prices.
EXAMPLE :
A survey regarding
the height (in cm) of 51 girls of class X of
a school was conducted and the following data was obtained:
|
Height in cm |
Number of Girls |
|
Less than 140 |
4 |
|
Less than 145 |
11 |
|
Less than 150 |
29 |
|
Less than 155 |
40 |
|
Less than 155 |
46 |
|
Less than 165 |
51 |
ANSWER
|
Height
(in cm) |
f |
C.F. |
|
below
140 |
4 |
4 |
|
140-145 |
7 |
11 |
|
145-150 |
18 |
29 |
|
150-155 |
11 |
40 |
|
155-160 |
6 |
46 |
|
160-165 |
5 |
51 |
N=51⇒N/2=51/2=25.5
As 29 is just greater than 25.5, therefore median class
is 145-150.
Median=l+ ![]()
×h
×h
Here,
l= lower limit of median class =145
C=C.F. of the class
preceding the median class =11
h= higher limit - lower
limit =150−145=5
f= frequency of median class =18
∴median=145+ ![]() ×5=145+4.03=149.03
×5=145+4.03=149.03
EXAMPLE :
The median of
the following data is 525. Find the values
of x and y,
if the total frequency is 100
|
Class interval |
Frequency |
|
0−100 |
2 |
|
100−200 |
5 |
|
200−300 |
x |
|
300−400 |
12 |
|
400−500 |
17 |
|
500−600 |
20 |
|
600−700 |
y |
|
700−800 |
9 |
|
800−900 |
7 |
|
900−1000 |
4 |
ANSWER
Computation of Median
|
Class
interval |
Frequency (f) |
Cumulative
frequency (cf) |
|
0-100 |
2 |
2 |
|
100-200 |
5 |
7 |
|
200-300 |
x |
7+x |
|
300-400 |
12 |
19+x |
|
400-500 |
17 |
36+x |
|
500-600 |
20 |
56+x |
|
600-700 |
y |
56+x+y |
|
700-800 |
9 |
65+x+y |
|
800-900 |
7 |
72+x
+ y |
|
900-1000 |
4 |
76+x
+ y |
|
Total
= 100 |
We
have,
N=∑fi=100
⇒76+x+y=100⇒x+y=24
It is given that the median is 525. Clearly, it lies in the class 500−600
∴l=500,h=100,f=20,F=36+x and N=100
Now,
Median=i+ ![]() ×h
×h
⇒525=500+ ![]() ×100
×100
⇒525−500=(14−x)×5
⇒25=70−5x⇒5x=45⇒x=9
Putting x=9 inx+y=24,
we get y=15.
Hence, x=9and y=15.