POLYNOMIAL

INTRODUCTION:

A polynomial is defined as an expression which contains two or more algebraic terms. It is made up of two terms namely Poly (meaning “many”) and Nominal (meaning “terms.”). Polynomials are composed of:

Constants such as 1, 2, 3, etc.

Variables such as g, h, x, y, etc.

Exponents such as 5 in x⁵ etc.

Example:

Find the degree of the polynomial 6s⁴+ 3x²+ 5x +19

Solution:

The degree of the polynomial is 4.

Geometrical Meaning of Zeroes of Polynomials

Geometrical Meaning of Zeroes of Polynomials:

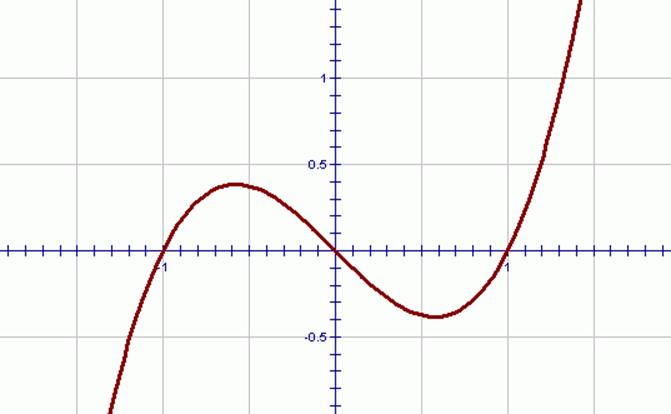
A real number k is said to be a zero of a polynomial p(x), if p(k) = 0.

Polynomials can easily be represented graphically.

Zero of polynomial p(x) is x-coordinate of point where graph of p(x) intersects x-axis.

Polynomial p(x) intersects the x-axis @ x=2, thus zero of this polynomial is 2.

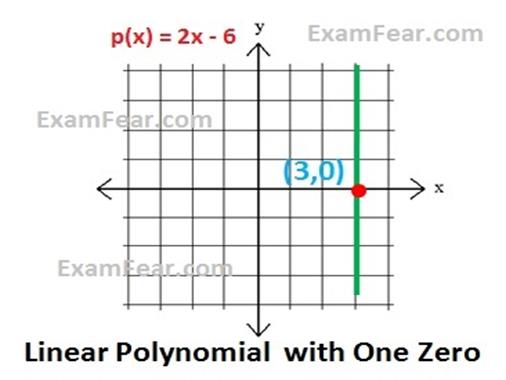
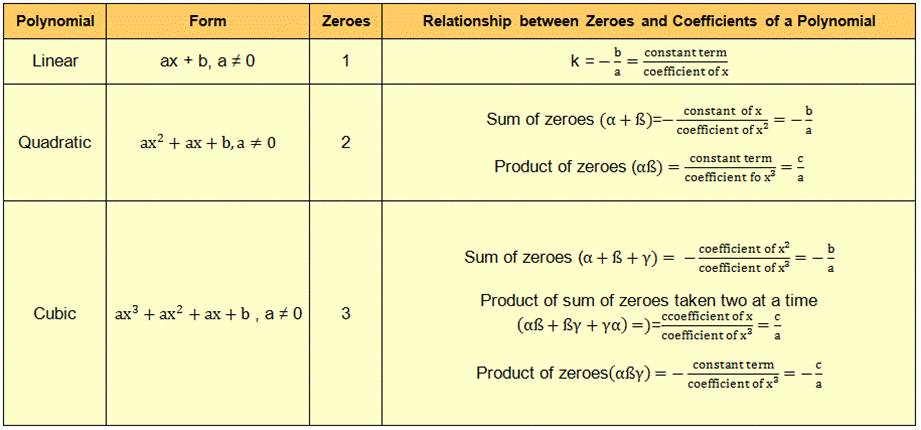
Linear polynomial ax + b, a ≠ 0, has exactly one zero

E.g.

Zero of linear polynomial p(x) = 2x -6   is 3 & thus the graph of this polynomial intersect x axis only once.

Relationship between Zeroes and Coefficients of a Polynomial:

A linear polynomial of the form P(x) = ax + b. If k is the zero of P(x), then,

P(k) = ak + b = 0

Zero of the polynomial, k = – b/a = – constant term/coefficient ofx

Now,

consider the quadratic polynomial, P(x) = 4x2−9x+2

Factorization of P(x) can be done by splitting the middle term into two terms such that their product is a multiple of the first term.

ie. multiple of 4x2. Middle term -9x can be written as,

−9x = −8x−x[−8x×−x=8x2=2×4x2]

4x2−9x+2 = 4x2−8x−x+2

= 4x(x−2)−(x−2)

= (4x−1)(x−2)

Zeros of the polynomial 4x2−9x+2 will be same as zeros of (4x−1)(x−2).

Zeros are found by equating the polynomial to zero.

(4x−1)(x−2) = 0

Therefore,

either (4x−1) = 0 or (x−2) = 0

4x – 1 = 0 gives x = 14 and x – 2 = 0 gives x = 2.

Zeros of P(x) are 14 and 2.

It is observed that, sum of zeros,

 14+2 = 94 = –coefficientofxcoefficientofx2

Product of the roots,1/4×2=1/2 = constant term/coefficient of x^2

Let’s take one more example to verify above concept, let P(x) = x2−3x−10.

To factorise the above polynomial, we have to split the middle term -3x into two terms such that the product of them is a multiple of −10x2.

Therefore,

-3x can be written as -3x =-5x + 2x, [since -5x × 2x = −10x2]

x2−3x−10 =x2−5x+2x−10

= x (x – 5) + 2(x – 5)

= (x – 5)(x + 2)

Zeros of P(x) are,

x – 5 = 0, x = 5

x + 2 = 0, x=-2

Sum of zeros,

5 – 2 = 31 = −coefficientofxcoefficientofx2

Product of zeros,

5 × -2 = – 101= constant term/coefficient of x^2

In general, if α and β are the zeros of the polynomial P(x)= ax2+bx+c,a≠0, then (x – α) and (x – β) are the factors of P(x).

P(x) can be written as,

ax2+bx+c=k(x−α)(x−β), where k is a constant.

= k[x2−(α+β)x+αβ]

=kx2−(α+β)kx+kαβ

Comparing the coefficients of terms gives,

a = k, b = -k(α + β), c = kαβ

It gives,

α + β= – bk =- ba

αβ = ck = ca

Therefore,

Sum of zeros,

α + β = – b/a = −coefficientofxcoefficientofx2

Product of zeros,

αβ = c/a =constanttermcoefficientofx2

Example 1:

Find a quadratic polynomial whose sum and product of zeros are 7 and 12.

Solution:

Let α and β be zeros of polynomial of form ax2+bx+c,

α + β = 7 = −ba

α + β = 12 = ca

If a = 1, then b = -7 and c = 12

Therefore, one quadratic polynomial satisfying the above condition is x2−7x+12

Now, consider the cubic polynomial P(x) = ax3+bx2+cx+d,a ≠ 0. If α,β,and γare zeros of P(x), then,

α + β + γ = –ba

αβ + βγ + αγ = ca

αβγ = –da

Example 2 :

Two zeros of the polynomial P(x) = x3−4x2+x+6 are 2 and -1. Find the third zero of P(x).

Solution:

Let the third root be γ,

Comparing polynomial with ax3+bx2+cx+d gives,

a = 1, b = -4, c = 1, d = 6

Sum of zeros of the cubic polynomial

2 – 1 + γ = −ba = 4

γ = 4 – 1 = 3

Division of a polynomial by polynomial:

For dividing a polynomial with another polynomial, the polynomial is written in standard form i.e. the terms of the dividend and the divisor are arranged in decreasing order of their degrees. Let us take an example.

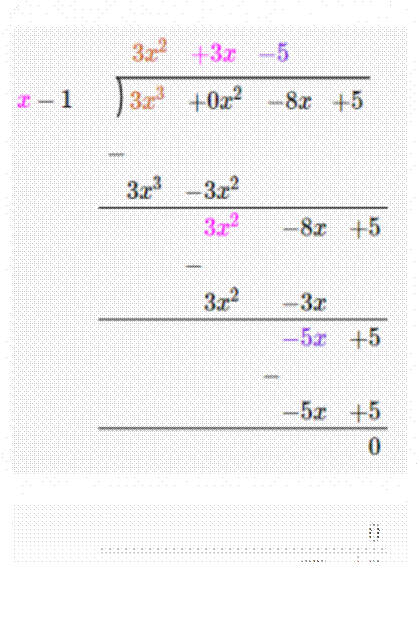
Example:

1.Divide 3x³ – 8x + 12 by x – 1.

Solution:

The Dividend is 3x³ – 8x + 12 and the divisor is x – 1.

After this, the leading term of the dividend is divided by the leading term of the divisor i.e. 3x³ ÷ x =3x². This result is multiplied by the divisor i.e. 3x²(x -1) = 3x³ -3x² and it is subtracted from the divisor. Now again, this result is treated as a dividend and the same steps are repeated until the remainder becomes zero or its degree becomes less than that of the divisor as shown below.