LINEAR EQUATIONS IN TWO VARIABLES DEFINITION

INTRODUCTION:

An equation that can be put in the form ax + by + c = 0, where a, b and c are real numbers and a, b not equal to zero is called a linear equation in two variables namely x and y. The solution for such an equation is a pair of values, one for x and one for y which further makes the two sides of an equation equal.

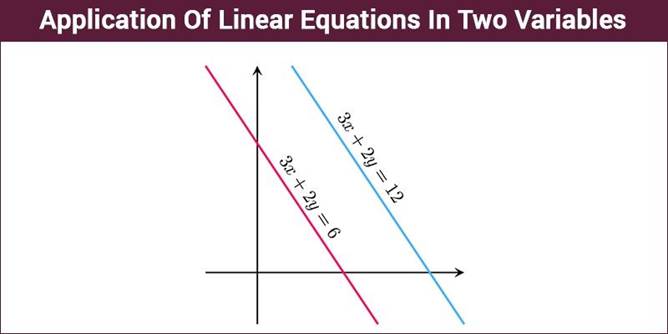
Let us take an example of a linear equation in two variables and understand the concept in detail.

LINEAR EQUATIONS IN TWO VARIABLES EXAMPLE:

In order to find the solution of Linear equation in 2 variables, two equations should be known to us.

Consider For Example:

1. 5x + 3y = 30

The above equation has two variables namely x and y.

Graphically this equation can be represented by substituting the variables to zero.

The value of x when y=0 is

5x + 3(0) = 30

⇒ x = 6

and the value of y when x = 0 is,

5 (0) + 3y = 30

⇒ y = 10

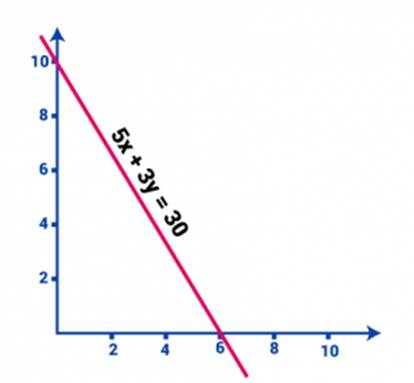
It is now understood that to solve linear equation in two variables, 2 equations have to be known and then the substitution method can be followed. Let’s understand this with a few example questions.

Linear Equations In Two Variables Questions :

Question:1

Find the value of variables which satisfies the following equation:

2x + 5y = 20 and 3x+6y =12.

Solution:

Using the method of substitution to solve the pair of linear equation, we have:

2x + 5y = 20…………………….(i)

3x+6y =12……………………..(ii)

Multiplying equation (i) by 3 and (ii) by 2, we have:

6x + 15y = 60…………………….(iii)

6x+12y = 24……………………..(iv)

Subtracting equation (iv) from (iii)

3y = 36

⇒ y = 12

Substituting the value of y in any of the equation (i) or (ii), we have

2x + 5(12) = 20

⇒ x = −20

Therefore,

x=-20 and y =12 is the point where the given equations intersect.

Now, it is important to know the situational examples which are also known as word problems from linear equations in 2 variables.

QUESTION:2

Akhila went to a fair in her village. She wanted to enjoy rides on the Giant Wheel and play Hoopla (a game in which you throw a rig on the items kept in the stall, and if the ring covers any object completely you get it). The number of times she played Hoopla is half the number of rides she had on the Giant Wheel. Each ride costs Rs 3, and a game of Hoopla costs Rs 4. If she spent Rs 20 in the fair, represent this situation algebraically and graphically.

Solution:

The pair of equations formed is:

Linear Equations In Two Variables Word Problems :

Question 1: 

A boat running downstream covers a distance of 20 km in 2 hours while for covering the same distance upstream, it takes 5 hours. What is the speed of the boat in still water?

Solution:

These types of questions are the real-time example of linear equations in two variables.

In water, the direction along the stream is called downstream. And, the direction against the stream is called upstream.

Let us consider the speed of a boat is u km/h and the speed of the stream is v km/h, then:

Speed Downstream = (u + v) km/h

Speed Upstream = (u – v) km/h

We know that

Speed = Distance/Time

So,

The Speed of boat when running downstream = (20⁄2) km/h = 10 km/h

The speed of boat when running upstream = (20⁄5) km/h = 4 km/h

From above, u + v = 10>…….(1)

u – v = 4 ………. (2)

Adding equation 1 and 2, we get: 2u = 1

u = 7 km/h

Also, v = 3 km/h

Therefore,

the speed of the boat in still water = u = 7 km/h

Question 2:

A boat running upstream takes 6 hours 30 minutes to cover a certain distance, while it takes 3 hours to cover the same distance running downstream. What is the ratio between the speed of the boat and speed of the water current respectively?

Solution:

If the speed downstream is a km/hr and the speed upstream is b km/hr, then

Speed in still water = a + b km/h

Rate of stream = ½ (a − b) kmph

Let the Boat’s rate upstream be x kmph and that downstream be y kmph.

Then,

distance covered upstream in 6 hrs 30 min = Distance covered downstream in 3 hrs.

⇒x × 6.5 hrs = y × 3hrs

⇒ 13/2x = 3y

⇒ y = 13x/6

The required ratio is = y+x2 : y–x2 ⇒ 13x6 + x2 : 13x6 − x2 ⇒ 19x62 : 7x62

= 19:7

GRAPHICAL METHOD OF SOLUTION OF A PAIR OF LINEAR EQUATIONS

We know that a linear equation in two variables represent a straight line. If we have the pair of equations that means we have two straight lines. Now the following possibilities are there:

1. Lines may intersect

2. Lines may be coincident

3. Lines may be parallel

i) When lines intersect in a single point we have one solution. Such solution is called a unique solution. (Consistent pair of equations).

ii) When lines are coincident every point on the lines is a solution so we have many solutions. [Dependent (consistent) pair of equations].

iii) When lines are parallel there is no common point satisfying both the equations. So we have no solution. (Inconsistent pair of equations).

The lines represented by the equation a1x+b1y+c1=0 and a2x+b2y+c2=0 are

i) intersecting, then a1a2≠b1b2.

ii) coincident, then a1a2=b1b2=c1c2.

iii) parallel, then a1a2=b1b2≠c1c2.

In fact, the converse is also true for any pair of lines.

Consistent and Inconsistent Linear Systems

In Economics, a line representing supply and a line representing demand are often graphed on the same coordinate plane, and the lines intersect at one point. How many solutions does this system of linear equations have? Is the system consistent, inconsistent, or consistent dependent? After completing this Concept, you'll be able to identify how many solutions a system of equations has and classify the system accordingly.

Guidance

Solutions to a system can have several forms:

One solution

No solutions

An infinite number of solutions

Inconsistent Systems

This Concept will focus on the last two situations: systems with no solutions or systems with an infinite amount of solutions.

A system with parallel lines will have no solutions.

Parallel lines will never intersect, so they have no solution.

A system with no solutions is called an inconsistent system.

Consistent Systems

Consistent systems, on the other hand, have at least one solution. This means there is at least one intersection of the lines. There are two cases for consistent systems:

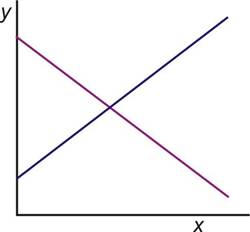
One intersection, as is commonly practiced in linear system Concepts

Infinitely many intersections, as with coincident lines

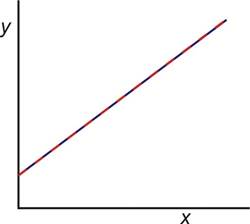
Coincident lines are lines that completely overlap.

The system has an infinite number of solutions. This is called a consistent-dependent system.

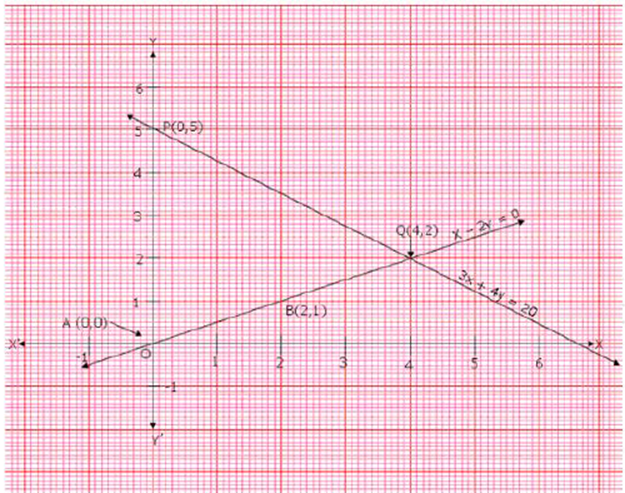
1. Check whether the pair of equations x+3y=6 . . . (1)

and 2x-3y=12 . . . (2) is consistent.

If so, solve them graphically.

Solution:

Line 1 àx+3y=6x+3y=6
If we put,

x=0, then

 y=2
If we put

 y=0,then

 x=6
So,

we can draw a line with points (0,2) and (6,0).

Line 2 -à2x−3y=122x-3y=12
If we put,

x=0, then y=−4
If we put

 y=0 then x=6
So,

we can draw a line with points (0,-4) and (6,0).


So, from the graph,

we can see that two lines intersecting at point (6,0)(6,0).

As, these lines have a unique solution at
x=6andy=0

This Pair Is Consistent.

ALGEBRAIC METHODS OF SOLVING A PAIR OF LINEAR EQUATION :

Algebraic Method :

An Algebraic method is a collection of several methods, which are used to solve a pair of the linear equation that includes two variables. Generally, the algebraic method can be sub-divided into three categories:

Substitution method

Elimination method

Cross-multiplication method

Substitution method:
1. The first step to solve a pair of linear equations by the substitution method is to solve one equation for either of the variables.
2. The choice of equation or variable in a given pair does not affect the solution for the pair of equations.
3. In the next step, we’ll substitute the resultant value of one variable obtained in the other equation and solve for the other variable.
4. In the last step, we can substitute the value obtained of the variable in any one equation to find the value of the second variable.

Solving Linear Equations by Substitution Method :

Let us understand the above theory of substitution using substitution method example

Consider the equations: 2x + 3y = 9 and x – y = 3

For solving simultaneous equations,

Let, 2x + 3y = 9……..(1) and x – y = 3 ……..(2)

From Equation (2)

we get, y = x – 3……………(3)

Now, as we understood above that in the substitution method, we find the value of one variable in terms of others and then substitute back.

Now,

we know that y = x – 3

Substituting the value of y in equation (1), we get

2x + 3y = 9

⇒ 2x + 3(x – 3) = 9

⇒ 2x + 3x – 9 = 9

⇒ 5x = 18

⇒ x = 185

Now, the value of y can be found out using equation (3)

So,

y = x – 3

⇒ y = 18/5  – 3

⇒ y = 35

Hence the solution of simultaneous equation will be:

x = 18/5  and y = 3/5

In this way, we can find out the value of the unknowns x and y using the substitution method.

Elimination method:
1. Multiply the equations with suitable non-zero constants, so that the coefficients of one variable in both equations become equal.
2. Subtract one equation from another, to eliminate the variable with equal coefficients.Solve for the remaining variable.
3. Substitute the obtained value of the variable in one of the equations and solve for the second variable.

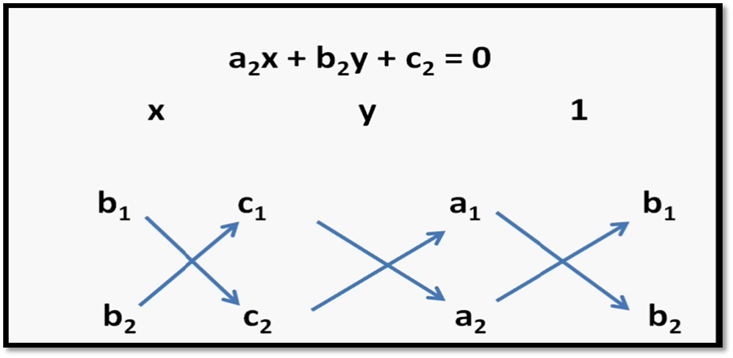
Cross - Multiplication Method:
Let’s consider the general form of a pair of linear equations a₁x + b₁y + c₁ = 0 , and a₂x + b₂y + c₂ = 0.
When a₁ divided by a₂ is not equal to b₁ divided by b₂, the pair of linear equations will have a unique solution.

Cross multiplication method:

Cross Multiplication Method :

Let’s assume that we have to find solution for 

a₁x + b₁y + c₁ = 0 (i)   and            

  a₂x + b₂y + c₂ = 0 (ii)

Step 1:

Multiply Equation (i) by b₂ and Equation (ii) by b₁, to get

b₂a₁x + b₂b₁y + b₂c₁ = 0    ---(iii)

b₁a₂x + b₁b₂ y + b₁c₂ = 0  ----(iv)

Step 2:

Subtracting Equation (4) from (3), we get:

(b₂a₁ – b₁a₂) x + (b₂b₁ – b₁b₂) y + (b₂c₁– b₁c₂) = 0

Or

(b₂a₁ – b₁a₂) x + (b₂c₁– b₁c₂) = 0

Or

x  = (b₁c₂– b₂c₁)/ (a₁b₂ – a₂b₁)

Step 3:

Substituting this value of x in (i) or (ii), we get

y = (c₁a₂ – c₂a₁)/ (a₁b₂ – a₂b₁)

Step 4:

Calculate value of a₁b₂ – a₂b₁

Step 5:

if a1b2 – a2b1 ≠ 0  or a1/a2 ≠ b1/b2, then equation has definite solution.

Step 6:

if a1b2 –a2b1 =0 or a1/a2 = b1/b2, then there are two possibilities

EQUATIONS REDUCIBLE TO PAIR OF LINEAR EQUATIONS IN 2 VARIABLES :

Sometimes we come across pair of equation which are not linear but can be reduced to linear form by making some suitable substitutions.

E.g. 

2/x + 3/y = 13     & 5/x + 4/y = 2

This equation is not a linear equation, but if we substitute 1/x with a & 1/y with b, then the equation becomes

2a+ 3b =13   & 5a + 4b = 2.

This is now a pair of linear equation in 2 variables.

After finding the values of variables a & b,

we can easily find x as 1/a & y as 1/b.