Quadratic Equations

Definition:

· A quadratic equation is any equation that can be rearranged in standard form as

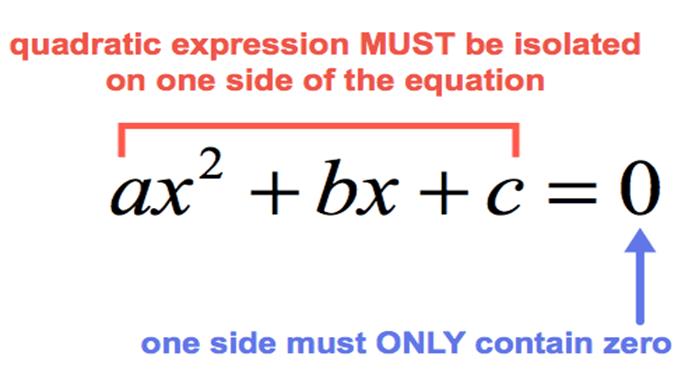
· The only requirement here is that we have an  in the equation. For this to be true a must not be equal to zero i.e. .

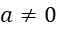· Note however, that it is okay if b and/or c are zero.

· Here x represents an unknown, and a, b, and c represent known numbers.

Hidden Quadratic Equations & Tracing a, b & c:

· Standard form of quadratic equation is given as

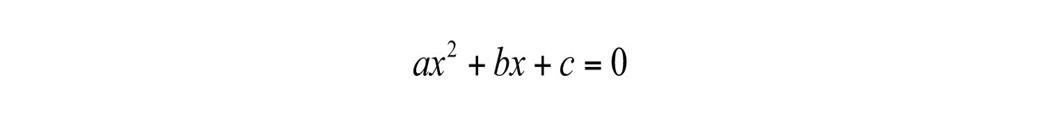
· But it does not always look like this, but we can rearrange the known and unknown terms and see if a given equation is quadratic or not

· After rearranging we can easily find the a, b & c terms of the quadratic equation, finding these terms will help us in solving the quadratic equation,

· The numbers a, b, and c are the coefficients of the equation and may be distinguished by calling them, respectively, a as the quadratic coefficient, b as the linear coefficient and c as the constant or free term.

Solving Quadratic Equations:

· The values of x that satisfy the equation(i.e. the values of x for which the left hand side(LHS) of the standard form is zero.) are called solutions of the equation, and roots or zeros of the quadratic equation.

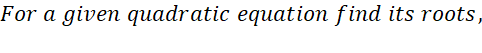
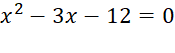
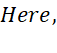
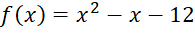
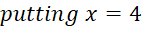
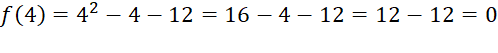
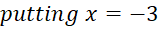
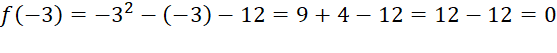
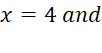
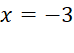
· A quadratic equation always has two solutions.

· There are many ways to solve quadratic equations. We will look at three of them. The first methods won’t always work yet are probably a little simpler to use when they work. The last two methods will always work, but often require a little more work or attention to get correct. let’s get started,

1^st Method: Solving by Factoring

· We will be solving quadratic equations here by factoring them. To do this we will need zero factor property or zero factor principle,

· All the fact says is that if a product of two terms is zero then at least one of the terms had to be zero.

· It may be possible to express a quadratic equation 

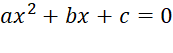
as a product 

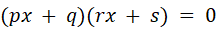
· Example for solving by factor

2^nd Method: Solving by Completing the Square

· The process of completing the square makes use of the formula,

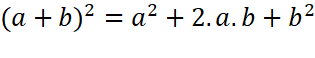
· Step 1: Start with a quadratic equation in standard form,

· Step 2: Divide each side by a, the coefficient of the squared term.

· Step 3: Subtract the constant term c/a from both sides.

· Step 4: Add the square of one-half of b/a, the coefficient of x, to both sides. This "completes the square", converting the left side into a perfect square.

· Step 5: Write the left side as a square and simplify the right side if necessary.

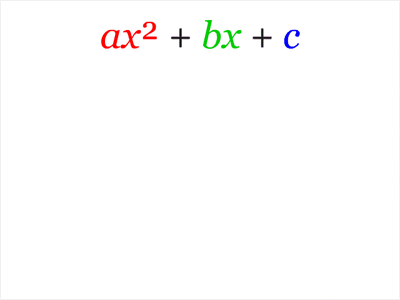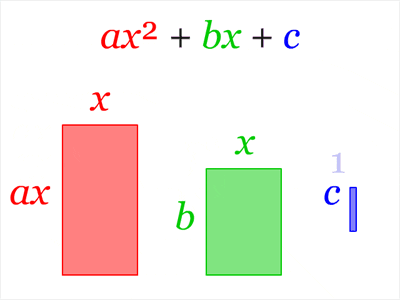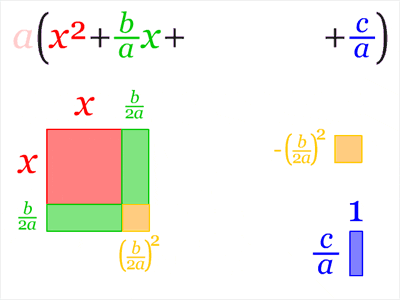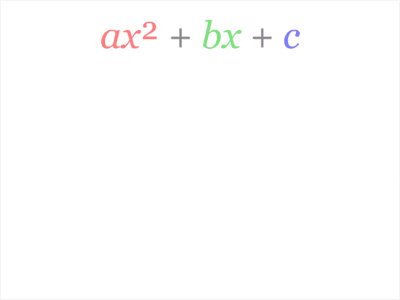
· Example of Completing square method,

3rd Method: Solving by Quadratic formula

· We can derive the quadratic formula by completing the square on the general quadratic formula in standard form.

· First, we MUST have the quadratic equation in standard form as already noted.

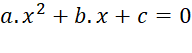
· Next, we need to divide both sides by aa to get a coefficient of one on the x² term.

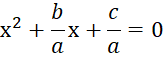
· Next, move the constant to the right side of the equation.

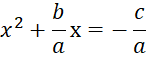
· Now, we need to compute the number we’ll need to complete the square. which is square of the one-half the coefficient of x,

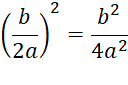
· Now, add this to both sides, complete the square and get common denominators on the right side to simplify things up a little.

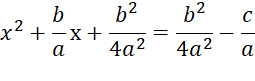
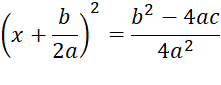
· Solve for x and we’ll also simplify the square root a little.

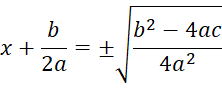
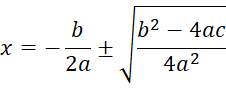
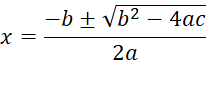
· The ± means there are TWO answers,

· Example on quadratic formula,

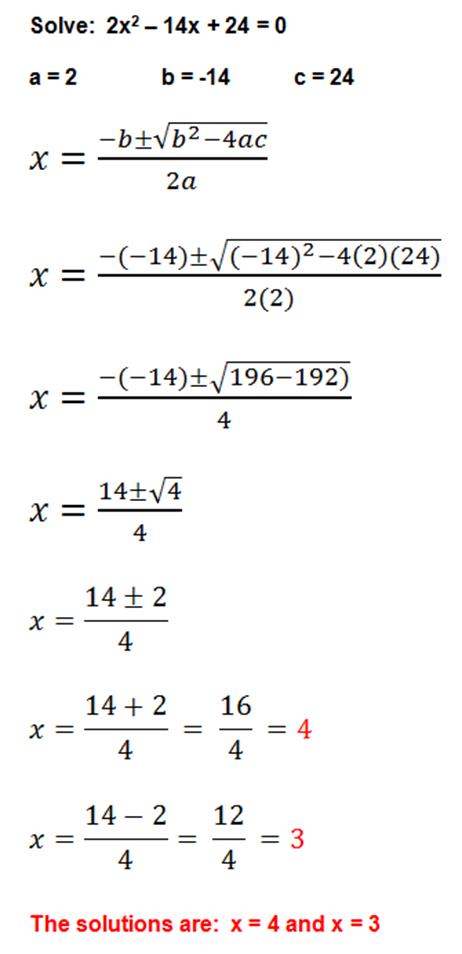
Nature of Roots:

· In the quadratic formula, the expression underneath the square root sign is called the discriminant of the quadratic equation, given as D,

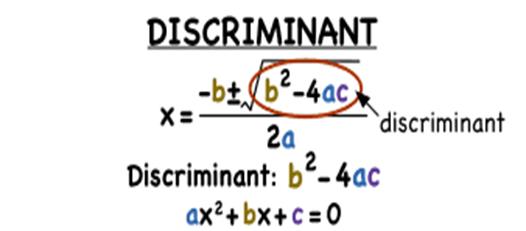
· The value of the discriminant that will determine the nature of the roots of the quadratic equations,

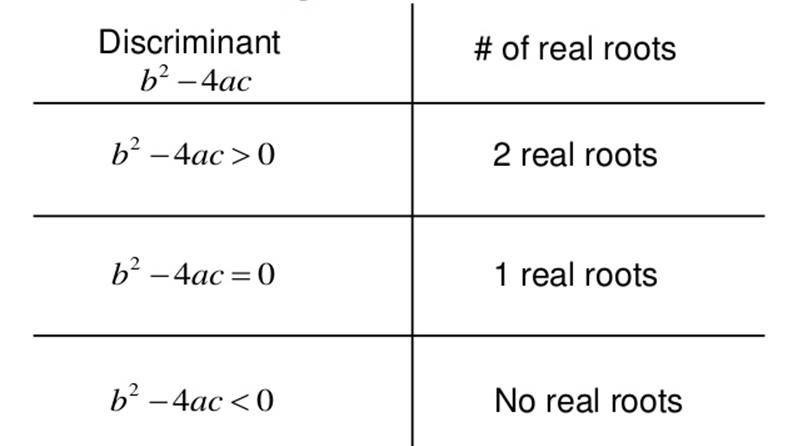
· 1^st Case
If 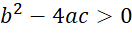 then we will get two real solutions to the quadratic equation.

· 2^nd Case
If 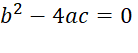 then we will get a double root to the quadratic equation.

· 3^rd Case
If 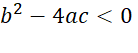then we will get no real solutions to the quadratic equation.

· Example on nature of roots,