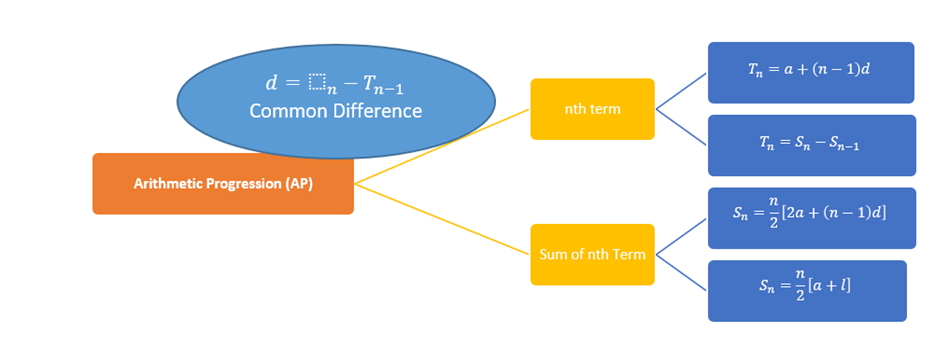
Arithmetic progression

Definition:

· In nature, many things follow a certain pattern or Sequence.

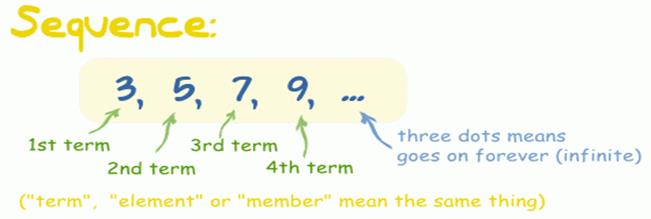
· Sequence: A Sequence is a set of things (usually numbers) that are in order.

· Each number in the sequence is called a term.

· Some more common sequence example,

Arithmetic Progression (AP):

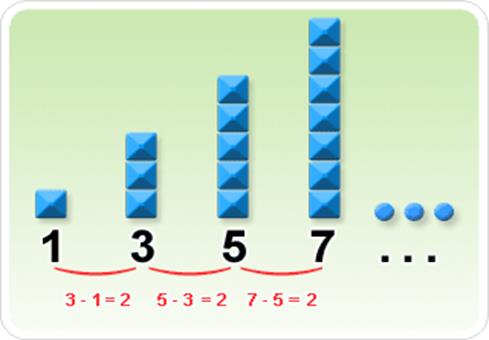
· An Arithmetic Progression (AP) or Arithmetic Sequence is a sequence of numbers such that the difference between the consecutive terms is constant.

· In General, we could write an arithmetic sequence like this,

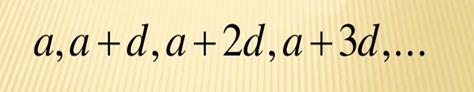
· Initial term/first term: In an arithmetic progression, the first number in the series is called the first term /initial term, here a is the first term.

· Common difference: The value by which consecutive terms increase or decrease is called the common difference. Here d is the difference between the terms.

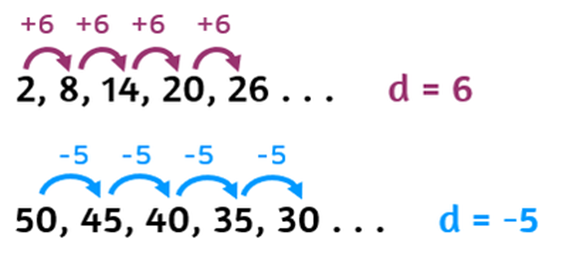
· If the common difference is positive, then the members (terms) will grow towards positive infinity.

· If the common difference is negative, then the members (terms) will grow towards negative infinity.

nth Term of an AP:

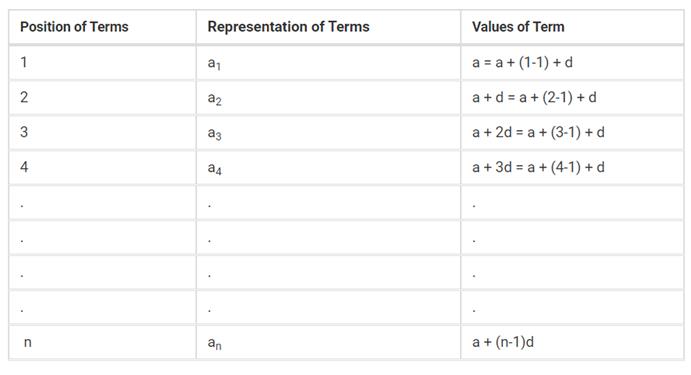
· The formula for finding the n-th term of an AP is,

· Consider an AP to be: a₁, a₂, a₃, ……………., a_n,

· Example on finding nth term,

Arithmetic Progression Sum Formula:

· For an AP, the sum of the first n terms can be calculated if the first term and the total terms are known or when first and last terms are given, The formula for the arithmetic progression sum is,

· Proof:

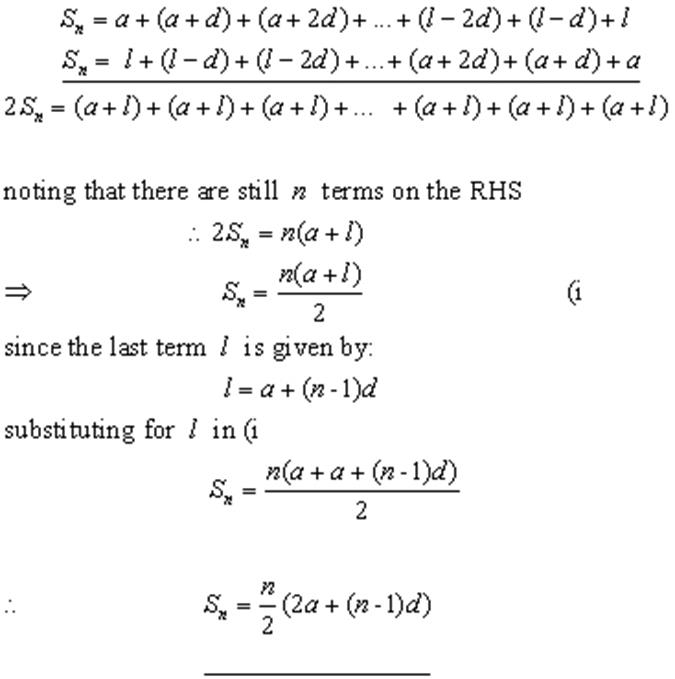
· Special Formula I:

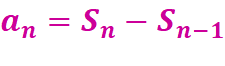
Proof:

· Special Formulas: Sum of first n natural numbers,

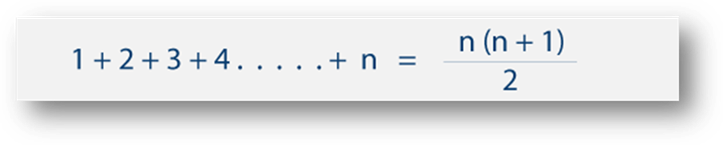
· Example on Sum of AP,

Summary: