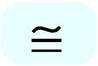Triangles

Any polygon which has three sides and three vertices is known as Triangle.

Types of Triangles

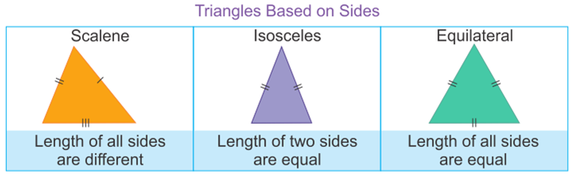
1. There are three types of Triangles on the basis of the length of the sides.

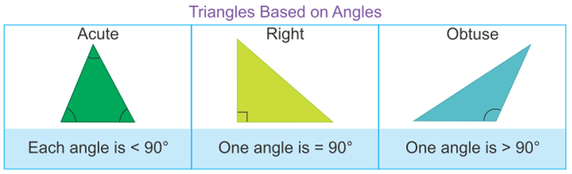
2. There are three types of Triangles on the basis of angles.

Centers of the Triangle

There are four different centers of the Triangle

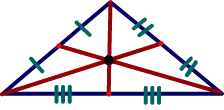
1. Centroid of a Triangle

The point of intersection of the medians of the three sides of the Triangle is the centroid of that Triangle. It will always inside the Triangle.

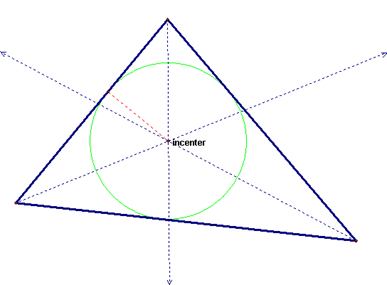
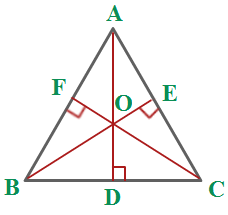
2. Incenter of a Triangle

The point of intersection of the angle bisectors of the three angles of the Triangle is called the incenter of that Triangle. It is the point from where the circle is inscribed in the Triangle.The radius is find by drawing the perpendicular from the incenter to any of the side of the Triangle.

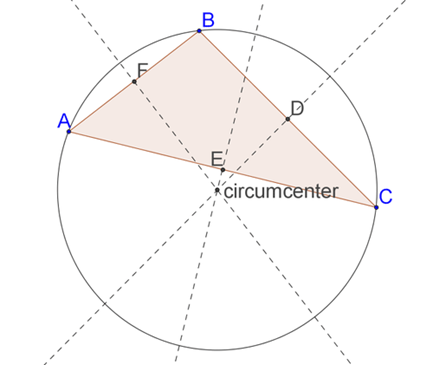
3. Circumcenter of the Triangle

The point of intersection of the perpendicular bisectors of the three vertices of the Triangle is called the circumcenter of that Triangle.It is not always inside the Triangle. It could be outside the Triangle for obtuse Triangle and fall at the midpoint of the hypotenuse of the right angled Triangle.

4. Orthocenter

The point of intersection of the altitudes of the Triangle is the orthocenter of that Triangle.Like circumcenter , it also falls outside the Triangle in case of obtuse Triangle and it falls at the vertex of the Triangle in case of right angle Triangle.

Congruent vs. Similar figures

	Congruent	Similar
Angles	Corresponding angles are same.	Corresponding angles are same.
Sides	Corresponding sides are same.	Corresponding sides are proportional.
Example
Explanation	Both the square have the same angles and same side.	Both the squares have same angles but not the same sides.
Symbols

The above explanation shows that if two figures are congruent then they will be similar also but it is not necessary that if two figures are similar then they will be congruent also.

Similarity of Triangles

In the Triangles also we will use the same condition that the two Triangles will be similar if-

· The corresponding angles of the two Triangles are same and

· The corresponding sides of the two Triangles are in same proportion.

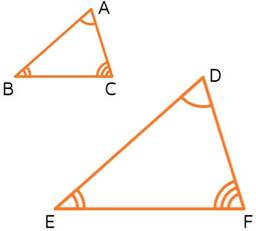
The above two Triangles ∆ABC and ∆DEF are similar as-

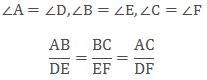
If the corresponding angles of the two Triangles are same then they are called equiangular Triangles.

Basic Proportionality Theorem (Thales Theorem)

According to Thales theorem, if in a given Triangle a line is drawn parallel to any of the sides of the Triangle so that the other two sides intersect at some distinct point then it divides the two sides in the same ratio.

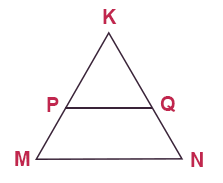
In ∆KMN, if PQ║MN and intersects KM at P and KN at Q, then,

Converse of Basic Proportionality Theorem

It is the opposite of basic proportionality theorem, which says that if in a given Triangle a straight line divides the two sides of the Triangle in the same ratio then that straight line is parallel to the third side of the Triangle.

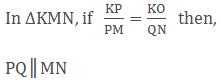
Criteria for the similarity of Triangles

Basically, there are three criteria to find the similarity of two Triangles.

1. AAA(angle-Angle-Angle) criteria of similarity

If in two given Triangles all the corresponding angles are equal then their corresponding sides will also be in proportion.

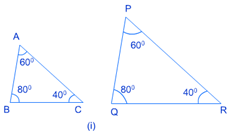
This shows that all the corresponding angles in the ∆ABC and ∆PQR are same so their corresponding sides are in proportion, that why the two Triangles similar.

Hence, ∆ABC ~ ∆PQR

Remark: If the two corresponding angles of the two Triangles are equal then according to the sum of angles of Triangle, the third angle will also be equal. So two Triangles will be similar if their two angles are equal with the two angles of another Triangle.This is known as AA (Angle-Angle) criteria.

2. SSS(Side-Side-Side) criteria of similarity

If in the two Triangles, all the sides of one Triangle are in same ratio with the corresponding sides of the other Triangle, then their corresponding angles will be equal. Hence the two Triangles are similar.

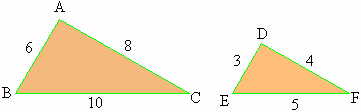
In ∆ABC and ∆DEF

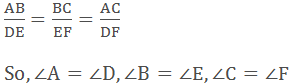
Hence, ∆ABC ~ ∆DEF

Remark: The above two criterions shows that if any of the two criteria satisfies then the other implies itself. So we need not check for both the conditions to satisfy to find the similarity of the two Triangles. If all the angles are equal then all the sides will be in proportion itself and vice versa.

3. SAS(Side-Angle-Side)criteria of similarity

If in the two Triangles, two sides are in the same ratio with the two sides of the other Triangle and the angle including those sides is equal then these two Triangles will be similar.

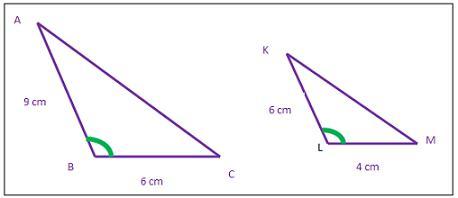
In ∆ABC and ∆KLM

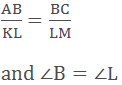
Hence, ∆ABC ~ ∆KLM

Areas of similar Triangles

If the two similar Triangles are given then the square of the ratio of their corresponding sides will be equal to the ratio of their area.

If ∆ABC ~ ∆PQR, then

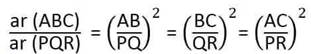
Pythagoras Theorem (Baudhayan Theorem)

Pythagoras theorem says that in a right angle Triangle, the square of the hypotenuse i.e. the side opposite to the right angle is equal to the sum of the square of the other two sides of the Triangle.

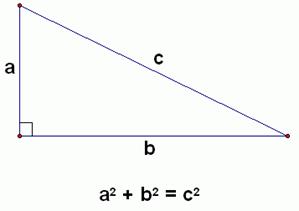
If one angle is 90°, then a² + b² = c²

Example

In the given right angle Triangle, Find the hypotenuse.

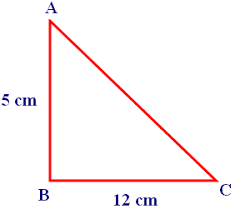
Solution

AB and BC are the two sides of the right angle Triangle.

BC = 12 cm and AB = 5 cm

From Pythagoras Theorem, we have:

CA² = AB² + BC ²

= (5)² + (12)²

= 25+144

So, AC² = 169

AC = 13 cm

Converse of Pythagoras Theorem

In a Triangle, if the sum of the square of the two sides is equal to the square of the third side then the given Triangle is a right angle Triangle.

If a² + b² = c² then one angle is 90°.

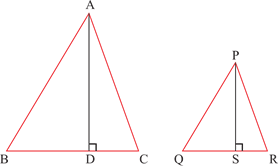
Similarity of two Triangles made in right angle Triangle

In a right angle Triangle, if we draw a perpendicular from the right angle to the hypotenuse of the Triangle, then both the new Triangles will be similar to the whole Triangle.

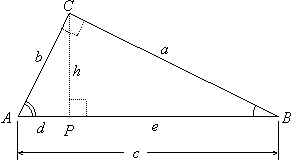
In the above right angle Triangle CP is the vertex on the hypotenuse, so

∆ACP ~ ∆ACB

∆PCB ~ ∆ACB

∆PCB ~ ∆ACP

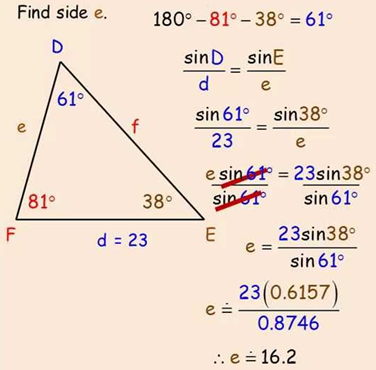
The laws of sines and cosines in a Triangle

The laws of sines and cosines are used to find the unknown side or angle of an oblique Triangle. Oligue Triangle is a Triangle which is not a right angle Triangle.

1. The law of sines

This shows the relation between the angle and the sides of the Triangle.

It is used when

i) Two angles and one side is given (AAS or ASA)

ii) Two sides and a non-included angle (SSA)

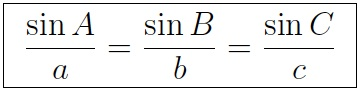
The law of sines shows that the sides of a Triangle are proportional to the sines of the opposite angles.

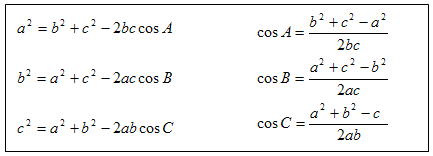
2. The law of cosine

It is used when

i) Two sides and an included angle is given(SAS)

ii) Three sides are given (SSS)