Coordinate Geometry

Cartesian Coordinate System

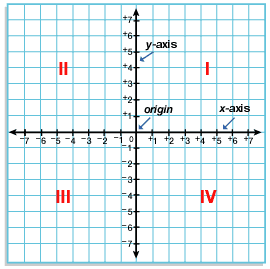
In the Cartesian coordinate system, there is a Cartesian plane which is made up of two  number lines which are perpendicular to each other, i.e. x-axis (horizontal) and y-axis (vertical) which represents the two variables. These two perpendicular lines are called the coordinate axis.

· The intersection point of these two lines is known as the center or the origin of the coordinate plane. Its coordinates are (0, 0).

· Any point on this coordinate plane is represented by the ordered pair of numbers. Let (a, b) is an ordered pair then a is the x-coordinate and b is the y-coordinate.

· The distance of any point from the y-axis is called its x-coordinate or abscissa and the distance of any point from the x-axis is called its y-coordinate or ordinate.

· The Cartesian plane is divided into four quadrants I, II, III and IV.

Equation of a Straight Line

An equation of line is used to plot the graph of the line on the cartesian plane.

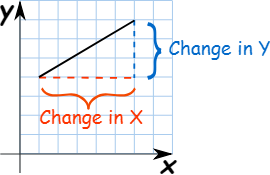
The equation of a line is written in slope intercept form as

y = mx +b

where m is the slope of the line and b is the y intercept.

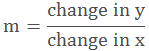
To find the slope of the line first we need to convert the equation in the slope intercept form then we can get the slope and y intercept easily.

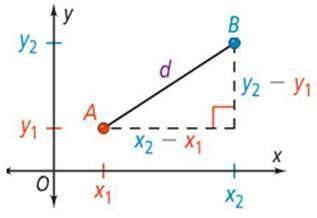
Distance formula

The distance between any two points A(x₁,y₁) and B(x₂,y₂) is calculated by

Example

Find the distance between the points D and E, in the given figure.

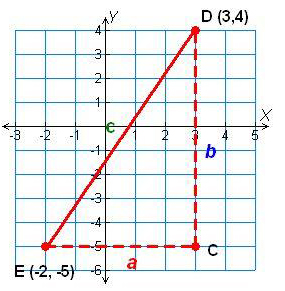
Solution

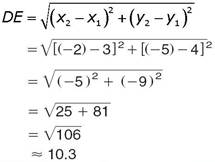
This shows that this is same as Pythagoras theorem. As in Pythagoras theorem

Distance from Origin

If we have to find the distance of any point from the origin then, one point is P(x,y) and the other point is the origin itself, which is O(0,0). So according to the above distance formula, it will be

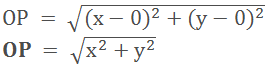
Section formula

If P(x, y) is any point on the line segment AB, which divides AB in the ratio of m: n, then the coordinates of the point P(x, y) will be

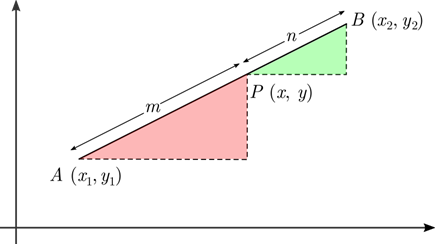
Mid-point formula

If P(x, y) is the mid-point of the line segment AB, which divides AB in the ratio of 1:1, then the coordinates of the point P(x, y) will be

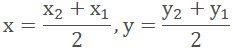
Area of a Triangle

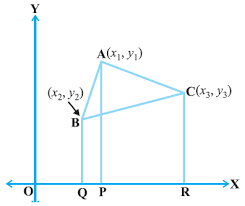
Here ABC is a triangle with vertices A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃). To find the area of the triangle we need to draw AP, BQ and CR perpendiculars from A, B and C, respectively, to the x-axis. Now we can see that ABQP, APRC and BQRC are all trapeziums.

Area of triangle ABC = Area of trapezium ABQP + Area of trapezium APRC – Area of trapezium BQRC.

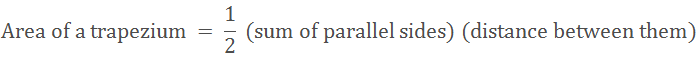
Therefore,

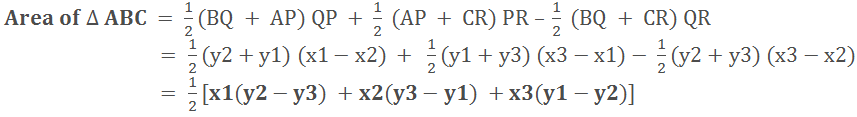
Remark: If the area of the triangle is zero then the given three points must be collinear.

Example

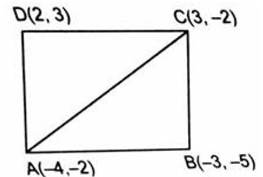
Let’s see how to find the area of quadrilateral ABCD whose vertices are A (-4,-2), B (-3,-5), C (3,-2) and D (2, 3).

If ABCD is a quadrilateral then we get the two triangles by joining A and C. To find the area of Quadrilateral ABCD we can find the area of ∆ ABC and ∆ ADC and then add them.

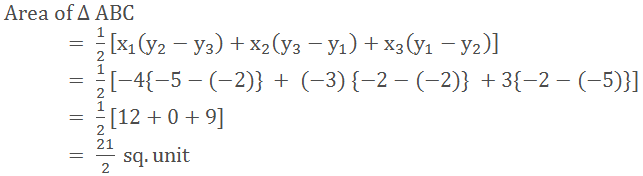
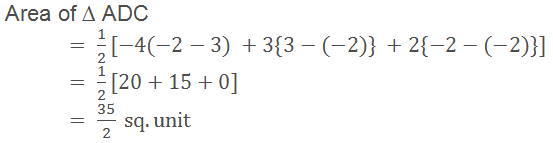
Area of a Polygon

Like the triangle, we can easily find the area of any polygon if we know the coordinates of all the vertices of the polygon.

If we have a polygon with n number of vertices, then the formula for the area will be

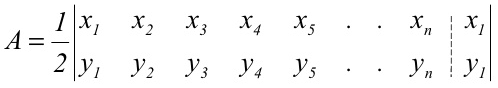
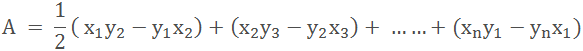
Where x₁ is the x coordinate of vertex 1 and y_n is the y coordinate of the nth vertex etc.

Example

Find the area of the given quadrilateral.

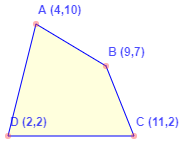
Solution

To find the area of the given quadrilateral-

· Make a table of x and y coordinates of each vertex. Do it clockwise or anti-clockwise.

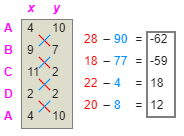
· Simplify the first two rows by:

o Multiplying the first row x by the second row y. (red)

o Multiplying the first row y by the second row x (blue)

o Subtract the second product form the first.

· Repeat this for all the other rows.

· Now add these results.

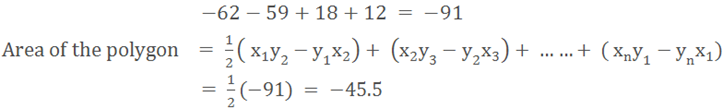
The area of the quadrilateral is 45.5 as area will always be in positive.

Centroid of a Triangle

Centroid of a triangle is the point where all the three medians of the triangle meet with each other.

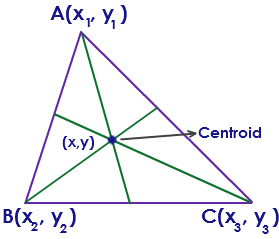
Here ABC is a triangle with vertices A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃). The centroid of the triangle is the point with the coordinates (x, y).

The coordinates of the centroid will be calculated as

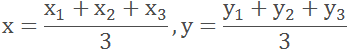
Remarks

In coordinate geometry, polygons are formed by x and y coordinates of its vertices. So in order to prove that the given figure is a:

No.	Figures made of four points	Prove
1.	Square	Its four sides are equal and the diagonals are also equal.
2.	Rhombus	Its four sides are equal.
3.	Rhombus but not square	Four sides are equal and the diagonals are not equal.
4.	Rectangle	Its opposite sides are equal and the diagonals are equal.
5.	Parallelogram	Its opposite sides are equal.
6.	Parallelogram but not a rectangle	Its opposite sides are equal but the diagonals are not equal.

No.	Figures made of three points	Prove
1.	A scalene triangle	If none of its sides are equal.
2.	An Isosceles triangle	If any two sides are equal.
3.	Equilateral triangle	If it’s all the three sides are equal.
4.	Right triangle	If the sum of the squares of any two sides is equal to the square of the third side.

Example

If the coordinates of the centroid of a triangle are (1, 3) and two of its vertices are (- 7, 6) and (8, 5), then what will be the third vertex of the triangle?

Solution

Let the third vertex of the triangle be P(x, y)

Since the centroid of the triangle is (1, 3)

Therefore,

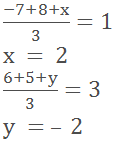
Hence the coordinate of the third vertex are (2, – 2).