Introduction to
Trigonometry
Introduction
From very ancient times surveyors, navigators and astronomers have
made use of triangles to determine distances that could not be measured directly.
This gave birth to the branch of mathematics what we call today as
“Trigonometry”.
Hipparchus of Rhodes around 200 BC(BCE),
constructed a table of chord lengths for a circle of circumference 360 × 60 = 21600 units which corresponds
to one unit of circumference for each minute of arc. For this achievement,
Hipparchus is considered as “The Father of
Trigonometry” since it became the basis for further
development.

Trigonometric Ratios
Let 0° < θ < 90°
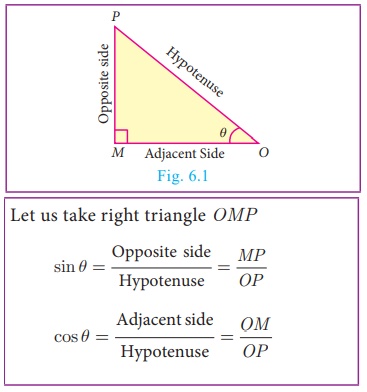
From the above two ratios we can obtain other four trigonometric
ratios as follows.
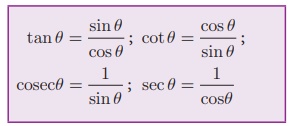
Note
All right triangles with θ as
one of the angle are similar. Hence the
trigonometric ratios defined through such right angle
triangles do not depend on the triangle chosen.
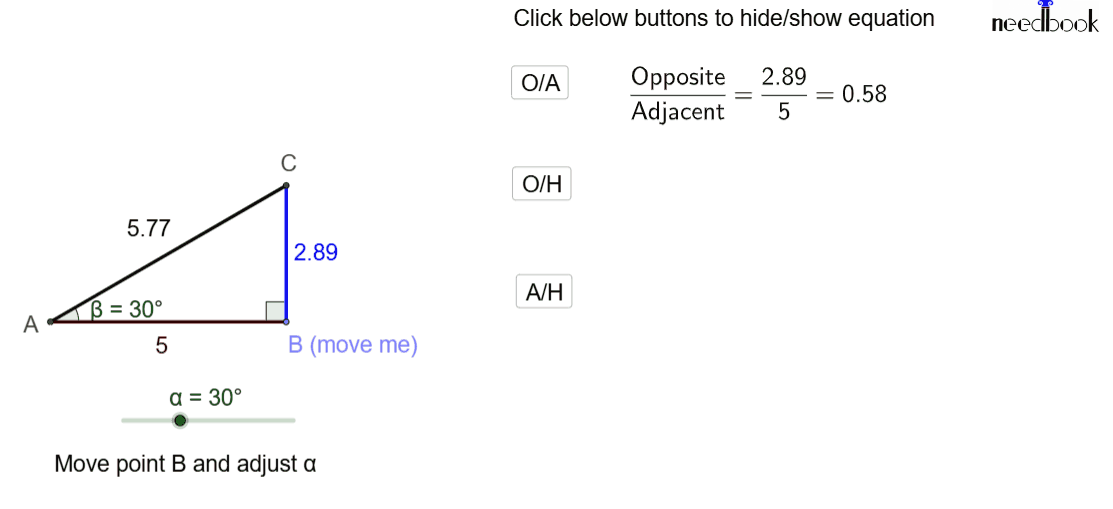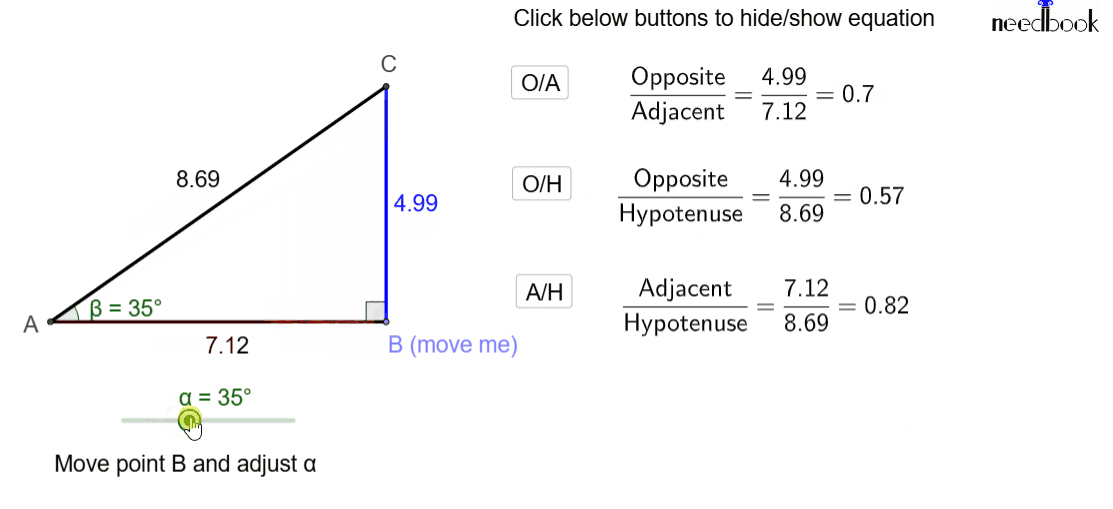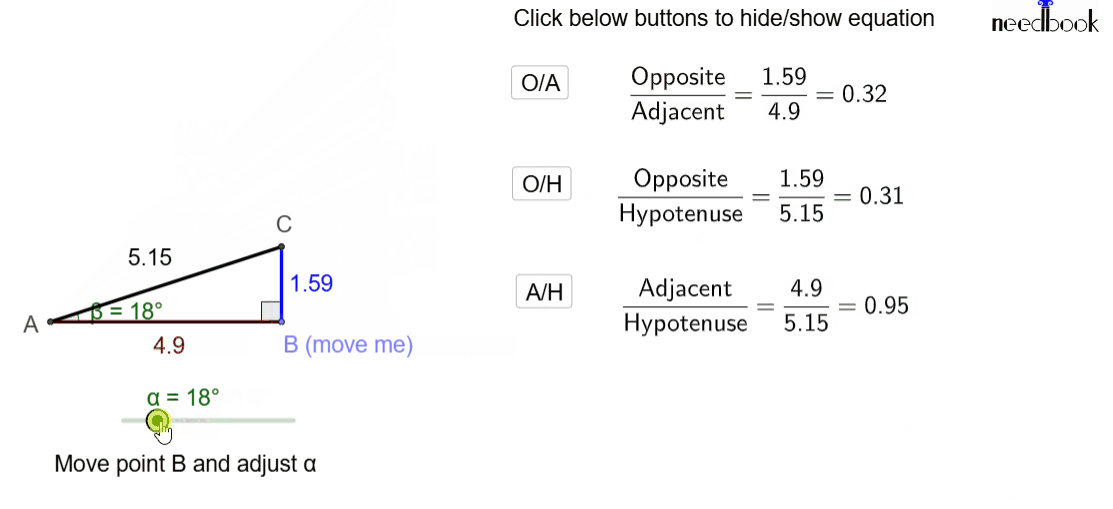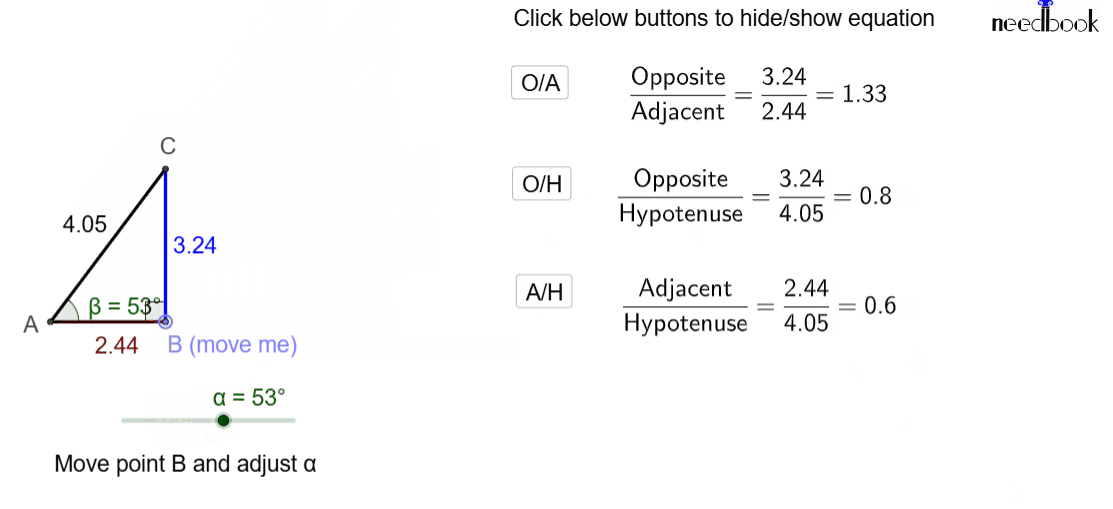
Practical Lab:


Complementary angle
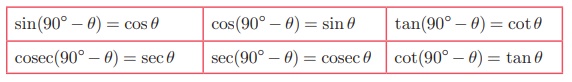
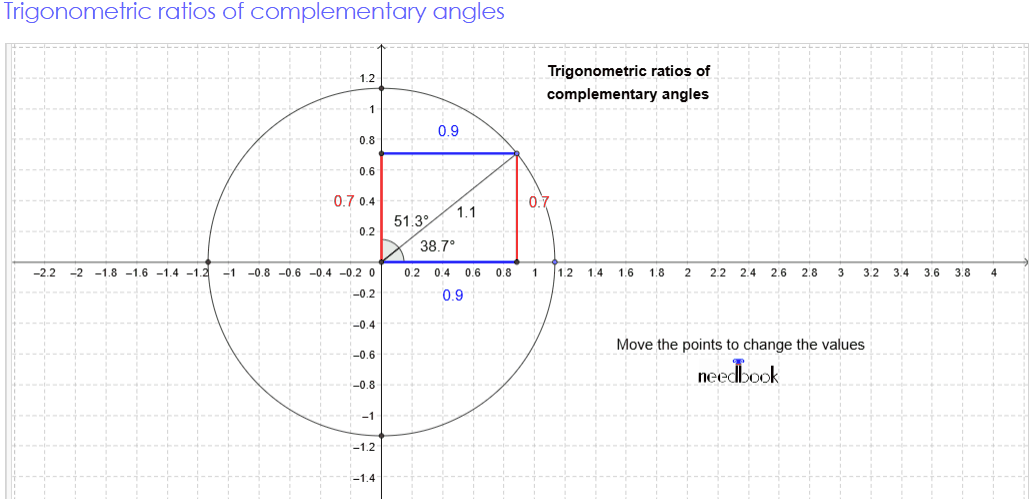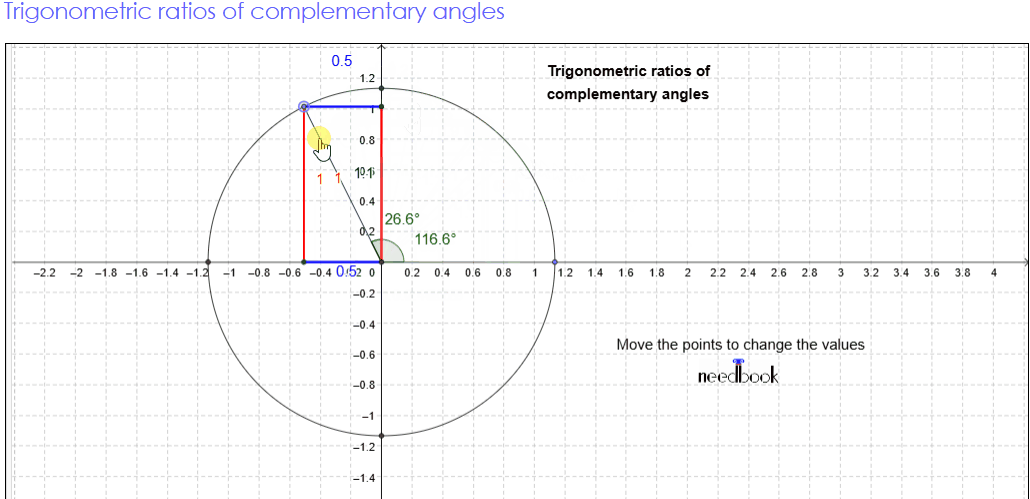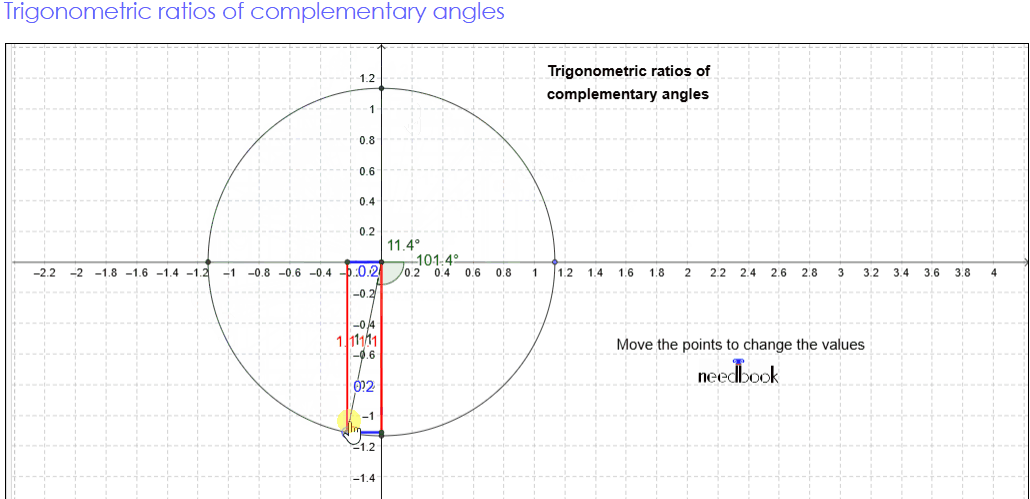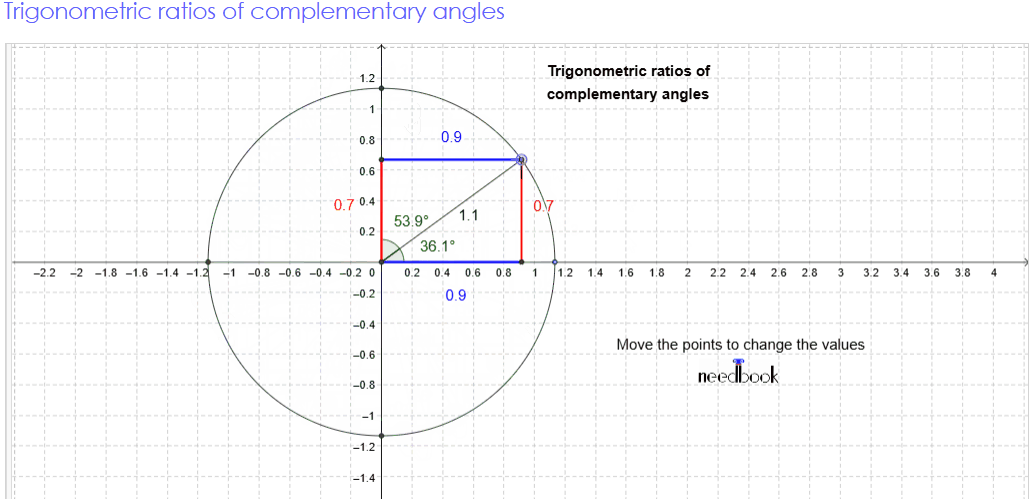
Visual proof of Trigonometric
complementary angle
Consider a semicircle of radius 1 as shown in the figure.
Let ∠QOP = θ.
Then ∠QOR =90° − θ, so
that OPQR forms a rectangle.
From triangle OPQ , OP/OQ = cos θ
But OQ = radius = 1
Therefore OP = OQ cos θ = cos θ
Similarly, PQ/OQ = sin θ
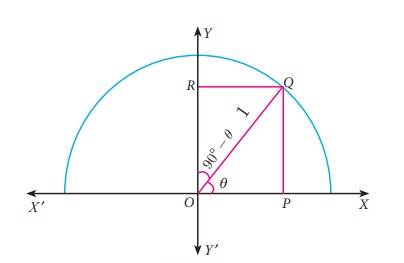
Gives, PQ = OQ sin θ = sin
θ (since OQ = 1)
OP = cosθ, PQ =
sinθ … (1)
Now, from triangle QOR,
we have OR/OQ = cos(90° − θ)
Therefore, OR = OQ cos(90° − θ)
So, OR = cos(90° − θ)
Similarly, RQ/OQ = sin(90°
− θ)
Then, RQ = sin(90° − θ)
OR= cos(90° − θ) , RQ = sin(90°
− θ) … (2)
Since OPQR is a rectangle,
OP = RQ and OR = PQ
Therefore from (1) and (2) we get,




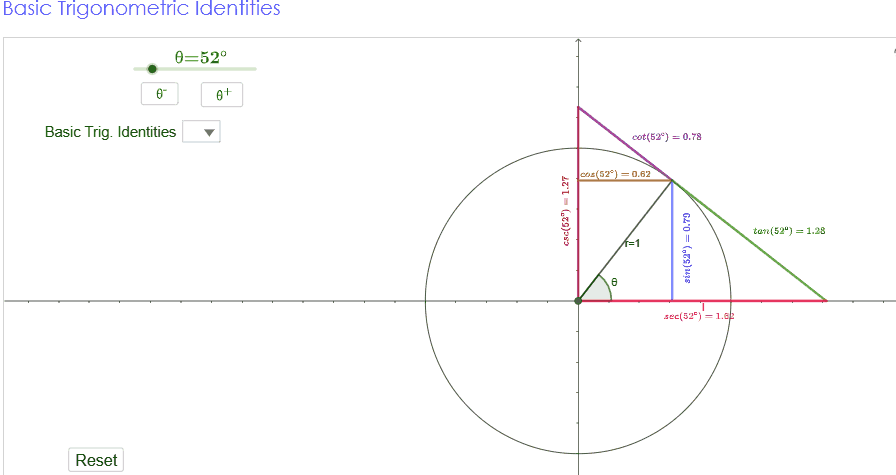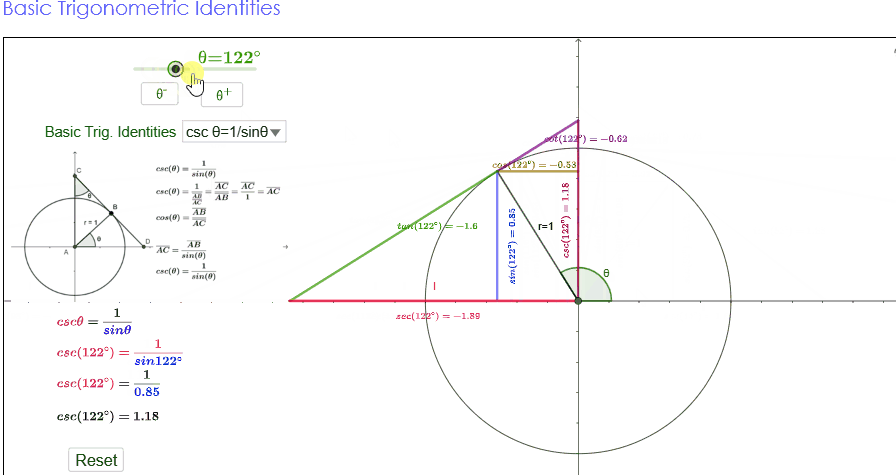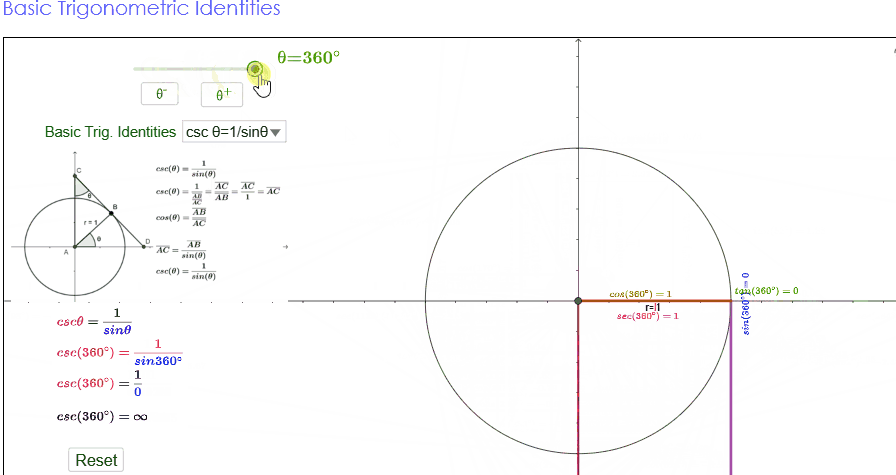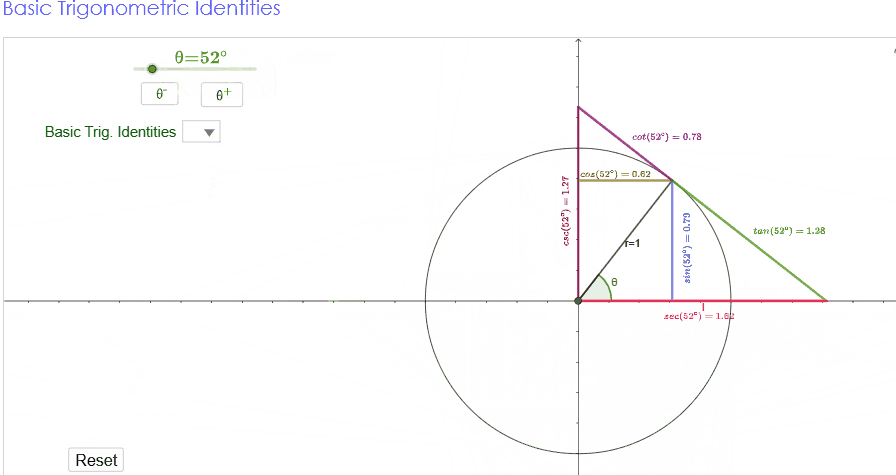
Trigonometric identities

For all real values of θ , we have
the following three identities.
(i) sin 2 θ +
cos2 θ=1
(ii) 1 + tan2 θ = sec2 θ
(iii) 1 + cot2 θ = cosec2 θ
These identities are termed as three fundamental identities of
trigonometry. We will now prove them as follows.

Practical Lab:
Practical Lab:


Example 6.1
Prove that tan 2 θ − sin2 θ = tan 2 θ
sin2 θ
Solution
tan 2 θ - sin2 θ = tan2 θ − 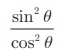 . cos2 θ
. cos2 θ
= tan 2 θ(1
− cos 2 θ) = tan 2 θ
sin2 θ
Example 6.2
Prove that 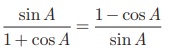
Solution
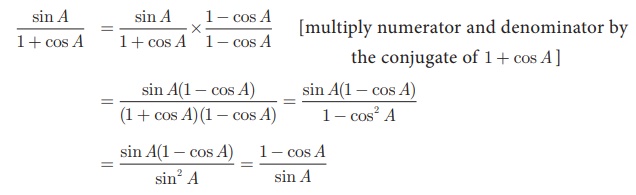
Example 6.3
Prove that 1 + 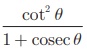 = cosec θ
= cosec θ
Solution
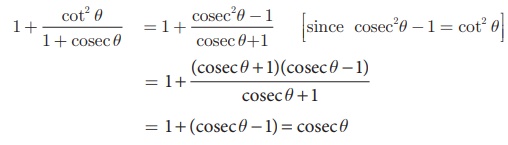
Example 6.5 Prove that 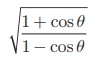 = cosec θ + cot θ
= cosec θ + cot θ
Solution
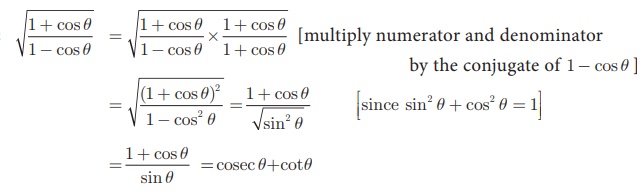
Example 6.6
Prove that 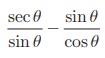 = cot θ
= cot θ
Solution
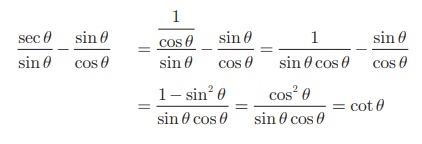
Example 6.14 Prove that 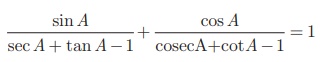
Solution

Example 6.16
Prove that 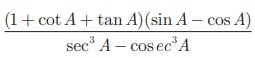 = sin 2 A cos2 A
= sin 2 A cos2 A
Solution

Example 6.17

Solution
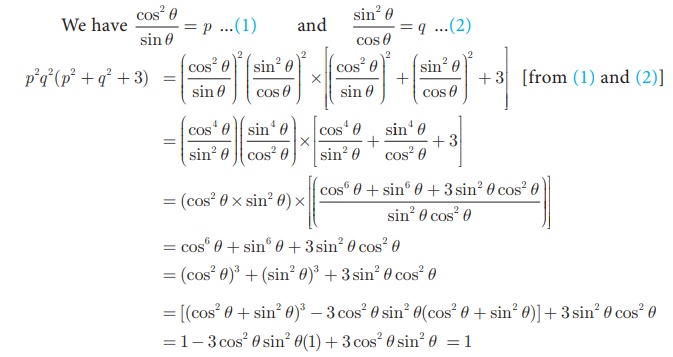
Trigonometric Ratios of Some Specific Angles :
For certain specific angles such as 30°, 45° and 60°, which are
frequently seen in applications, we can use geometry to determine the
trigonometric
Trigonometric Ratios of
30° and 60°

Let ABC be an equilateral triangle whose sides have length a (see
the figure given below). Draw AD perpendicular to BC, then D bisects the side
BC.
Then,
BD = DC = a/2
∠BAD = ∠DAC = 30°
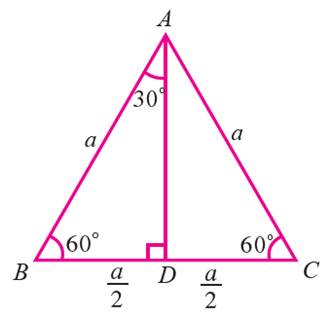
Now, in right triangle ADB, ∠BAD = 30° and BD = a/2.
In right triangle ADB, by Pythagorean
theorem,
AB2 = AD2 + BD2
a2 = AD2 + (a/2)2
a2 - (a2/4) = AD2
3a²/4
= AD2
√(3a2/4) = AD
√3 ⋅ a/2 = m AD
Hence, we can find the trigonometric ratios of angle 30° from the right triangle ADB.
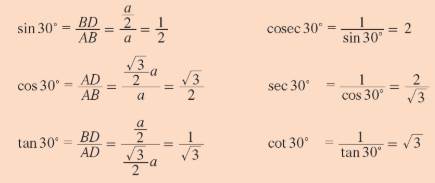
In right triangle ADB, <ABD = 60°. So, we can determine the
trigonometric ratios of angle 60°.
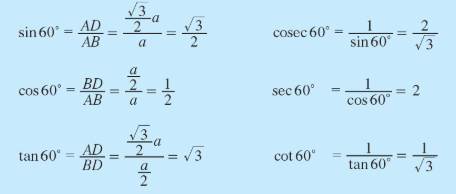
Trigonometric Ratio of
45°

If an acute angle of a right triangle is 45°, then the other acute
angle is also 45°.
Thus the triangle is
isosceles. Let us consider the triangle ABC with
∠B = 90°
∠A = ∠C = 45°
Then AB
= BC.
Let AB
= BC = a.
By Pythagorean theorem,
AC2
= AB2 + BC2
AC2
= a2 + a2
AC2
= 2a2
Take square root on each side.
AC = a√2
Hence, we can find the trigonometric ratios of angle 45° from the
right triangle ABC.
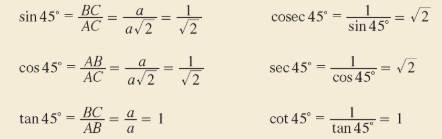
Trigonometric Ratios of
0° and 90°

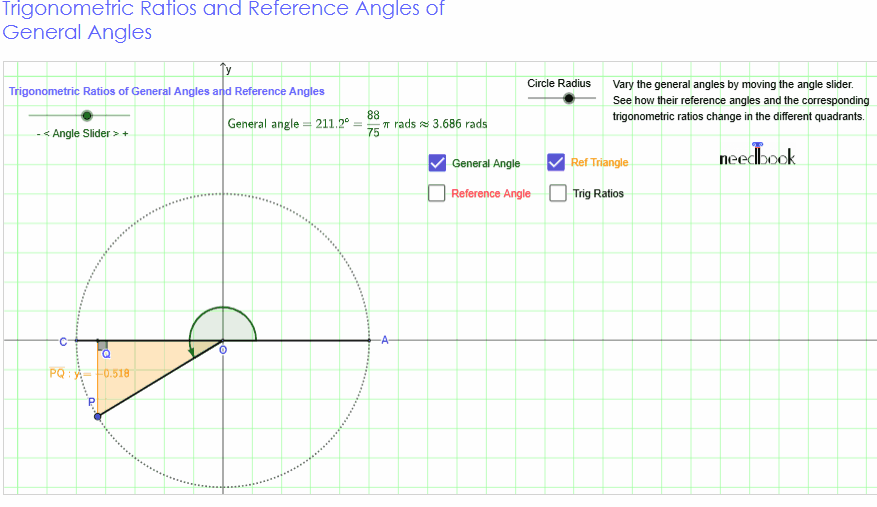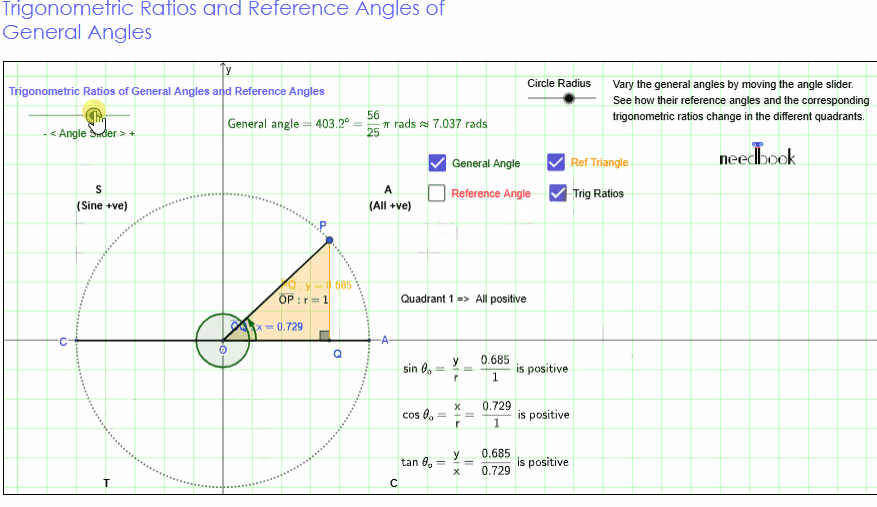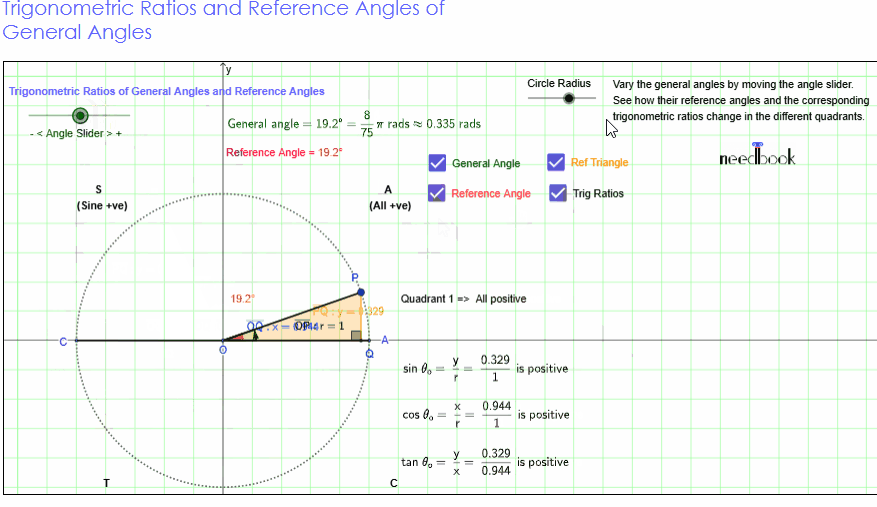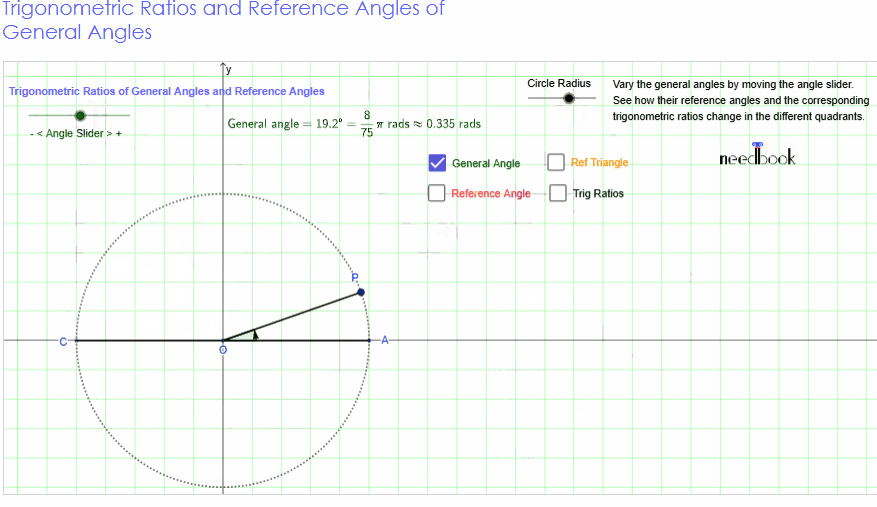
Consider the figure given below which shows a circle of radius 1
unit centered at the origin.
Let P be a point on the circle in the first quadrant with
coordinates (x, y).
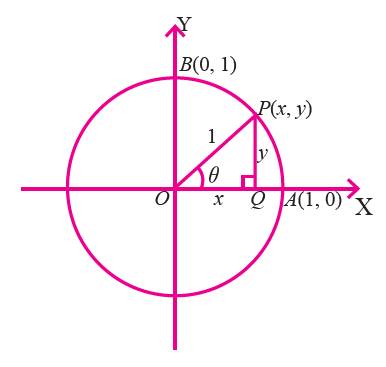
We drop a perpendicular PQ
from P to the x-axis in order to form the right triangle OPQ.
Let ∠POQ = θ, then
sin θ
= PQ / OP = y/1 = y (y
coordinate of P)
cos θ
= OQ / OP = x/1 = x (x
coordinate of P)
tan θ
= PQ / OQ = y/x
If OP coincides with OA,
then angle θ = 0°.
Since, the coordinates of A
are (1, 0), we have

If OP coincides with OB,
then angle θ = 90°.
Since, the coordinates of B are (0, 1), we have
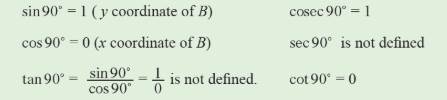
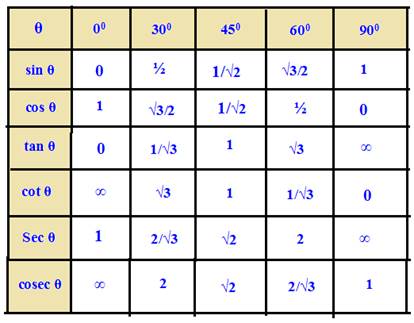
The six trigonometric
ratios of angles 0°, 30°, 45°,
60° and 90° are provided in the following table.
Practical Lab:
Trigonometric Ratios of Complementary
Angles
We know that complementary angles are the set of two angles
such that their sum is equal to 90°. For example
30° and 60° are complementary to each other as their sum is equal to 90°.
Thus, two angles X and Y are complementary if,
∠X + ∠Y = 90°
In such a condition ∠X is
known as the complement of ∠Y and
vice-versa.
Practical Lab:
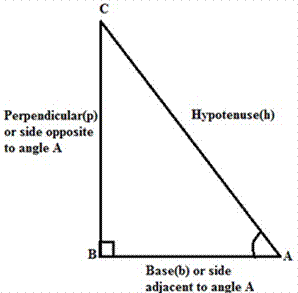
In a right angle triangle, as the
measure of the right angle is fixed, the remaining two angles are always
complementary as the sum of angles in a triangle is 180°.
The given triangle ∆ABC is right-angled at B; ∠A and ∠C form a
complementary pair.
⇒ ∠A + ∠C = 90°
The relationship between the acute angle and the lengths of
sides of a right-angle triangle is expressed by trigonometric
ratios.
For the given right angle triangle, the
trigonometric ratios of ∠A is
given as follows:
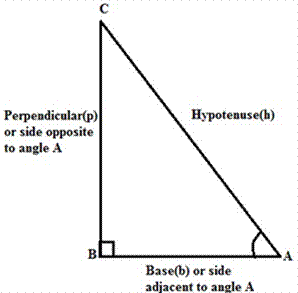
sin A = BCAC
cos A = ABAC
tan A = BCAB
csc A = 1sin A = ACBC
sec A = 1cos A = ACAB
cot A = ABBC
The trigonometric ratio of the complement of ∠A i.e., ∠C can be given as:
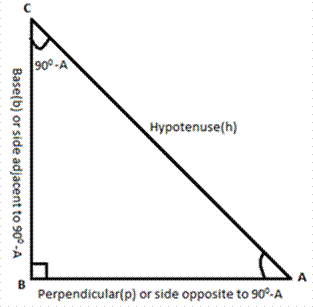
As ∠C = 90°- A (A is used for convenience
instead of ∠A ), and the side opposite to 90° – A is
AB and the side adjacent to the angle 90°- A is BC as shown in the figure given
above.
Therefore,
sin (90°- A) = ABAC
cos (90°- A) = BCAC
tan (90°- A) = ABBC
csc (90°- A) = 1sin (90° − A) = ACAB
sec (90°- A) = 1cos (90° − A) = ACBC
cot (90°- A) = BCAB
Comparing the above set of ratios with the ratios mentioned
earlier, it can be seen that;
sin (90°- A) = cos A ; cos (90°-
A) = sin A
tan (90°- A) = cot A; cot (90°- A) = tan A
sec (90°- A) = csc A; csc (90°- A) = sec A
These relations are valid for all the values of A lying between
0° and 90°.
Summary:
·
Sin of an angle = Cos of its complementary angle
·
Cos of an angle = Sin of its complementary angle
·
Tan of an angle = Cot of its complementary angle