Some Applications of Trigonometry

TRIGONOMETRY APPLICATIONS IN REAL LIFE:

It may not have direct applications in solving practical issues but used in the various field. For example, trigonometry is used in developing computer music: as you are familiar that sound travels in the form of waves and this wave pattern through a sine or cosine function for developing computer music. Here are a few applications where trigonometry and its functions are applicable.

Heights and Distances

To find the height of an object or to find the distance of an object to the other we must know the meaning of some points -

Line of Sight

When we look at some object then the line made by our vision to the object is called the Line of Sight.

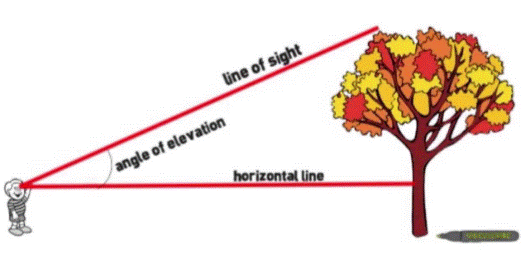
Horizontal Line

A horizontal line is a distance between the observer and the object.

Angle of Elevation

An angle of elevation is the angle made by the line of sight to the top of the object and the horizontal line. It is above the horizontal line i.e. the angle of elevation is made when we look up to the object.

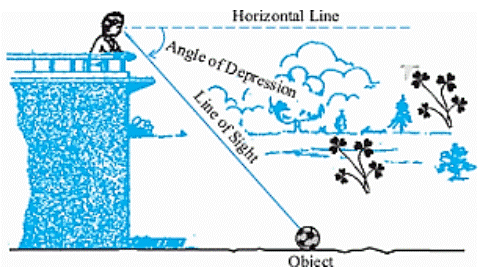
Angle of Depression

An angle of depression is made when the observer needs to look down to see the object.The angle between the horizontal line and the line of sight is the angle of depression when the horizontal line is above the angle.

Some Solved Examples

To solve the problems related to the angle of elevation and angle of depression we must remember trigonometric ratios, trigonometric table and the trigonometric identities.

Example: 1

Find the height of the flagpole if the angle of elevation is 30° and the distance of flag from the observer is 15 m.

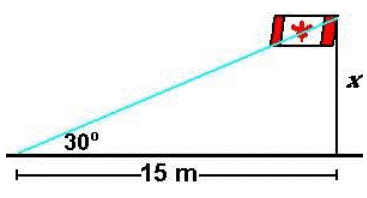
Solution:

Let x be the height of the flagpole.

Horizontal line is 15m.

Now, to calculate x, we need to take the trigonometric ratio which includes perpendicular and base.

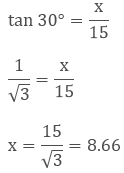
Hence, the flagpole is 9 m.

Example: 2

A child was playing at the top of the hill. He had thrown a stone in the lake from the hill, the distance covered by the stone was 150 m and the angle of depression was 30°, then what is the height of the hill?

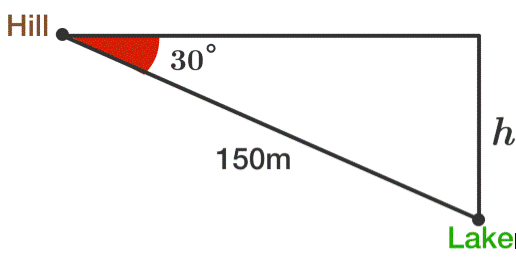
Solution:

Let the height of the hill be h.

The hypotenuse is 150 m and the angle of depression is 30°.

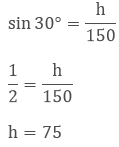
Hence the height of the hill is 75 m.

Example: 3

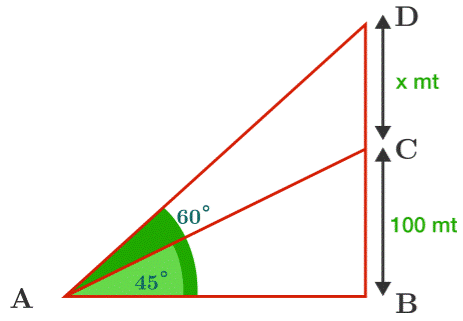
A person standing at point A is looking up at the angle of elevation of 45° to the aeroplane which is at the height of 100 m. As the airplane is going upwards, after some, the person was looking at the angle of elevation of 60°. Then what will be the increase in the height of the aeroplane from the ground at the angle of 60°?

Solution:

Given

∠CAB = 45°, ∠DAB = 60°

Distance of the aero plane from the ground = x + 100 m

In ∆ABC

AB = BC = 100 m

In ∆ABD

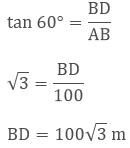
BD = BC + CD

100√3m = 100 + x

x = 100(√3 - 1) m

Hence, the increase in the height of the aero plane is100 (√3 -1) m.

Example: 4

A girl who is 1.2 m tall is watching a ballon moving in a horizontal line at a height of 88.2 m from the ground.The angle of elevation from her eyes is changed from 60° to 30°. Calculate the distance travelled by balloon.

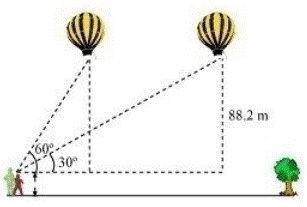
Solution:

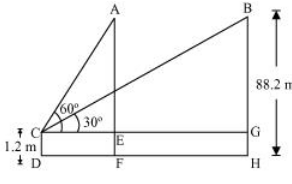In ΔACE

In ΔBCG

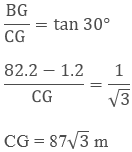
CG = 87√3 m

Distance travelled by ballon = EG = CG - CE

87√3 - 29√3 = 58√3 m