Conic Sections
Introduction:
The curves
parabola, hyperbola, ellipse and circle are
in fact, known as conic
sections or more commonly conics because
they can be obtained as intersections of a plane with a double napped right
circular cone. These curves have a very wide range of applications in fields
such as planetary motion, design of telescopes and antennas, reflectors in
flashlights and automobile headlights, etc.
Section of a Cone:
Let
l be a fixed vertical line and m be another line
intersecting it at a fixed point V and inclined to it at an angle
![]() . Suppose we rotate the line m around the line l in
such a way that the angle a remains constant. Then the surface generated is a double-napped
right circular hollow cone.
. Suppose we rotate the line m around the line l in
such a way that the angle a remains constant. Then the surface generated is a double-napped
right circular hollow cone.
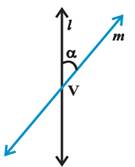
Here, point V is called
the vertex,
Line l is the axis of the cone,
Rotating line m is called a generator of the cone.
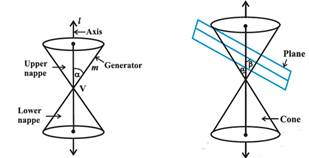
Intersection of a plane
with a cone is called a conic section. We
obtain different kinds of conic sections depending on the position of the intersecting
plane with respect to the cone and by the angle made by it with the vertical axis
of the cone. Let ![]() be
the angle made by the intersecting plane with the vertical axis of the cone.
be
the angle made by the intersecting plane with the vertical axis of the cone.
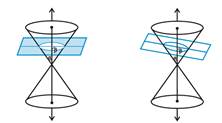
When the plane cuts the nappe (other than the vertex) of
the cone, we have the following situations:
(a) When ![]() =
90
=
90![]() , the section is a circle.
, the section is a circle.
(b) When ![]() <
<
![]() <
90
<
90![]() , the section is an ellipse.
, the section is an ellipse.
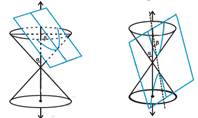
(c) When
![]() ; the section is a parabola.
; the section is a parabola.
(d) When
![]() ; the plane cuts through both the nappes and the curves of intersection
is a hyperbola.
; the plane cuts through both the nappes and the curves of intersection
is a hyperbola.
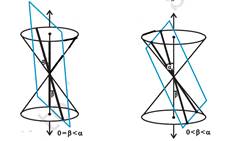
When
the plane cuts at the vertex of the cone, we have the following different
cases:
(a) When![]() , then the section is a point .
, then the section is a point .
(b) When
![]() , the plane contains a generator of the cone and the section is a
straight line. It is the degenerated case of a parabola.
, the plane contains a generator of the cone and the section is a
straight line. It is the degenerated case of a parabola.
(c) When
![]() , the section is a pair of intersecting straight lines. It is the
degenerated case of a hyperbola.
, the section is a pair of intersecting straight lines. It is the
degenerated case of a hyperbola.
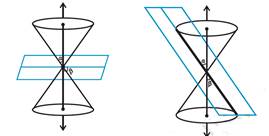
Circle:
ü
A circle is the
set of all points in a plane that are equidistant from a fixed point in the
plane.
ü
The fixed point is called the centre of the circle and the distance from the centre to a point on the circle is
called the radius of the circle.
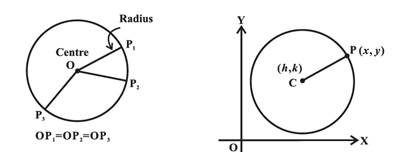
ü
Standard form of
equation of a circle: ![]()
where,
(h,k) is the centre of the
circle and r is radius of circle.
ü Simplest form of equation of a circle:![]()
where, (0,0) is the centre of the circle and r is the radius of the
circle.
ü General form of equation of a circle: ![]()
where,
(-g, -f) is the centre of the circle and ![]() is the radius of the
circle.
is the radius of the
circle.
Question 1: Find the equation
of the circle with centre (5,-2) and radius 3.
Solution:
Here, h=5, k=-2 and r=3
The
equation of the circle is
![]()
![]()
![]()
![]()
![]()
![]()
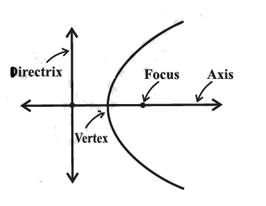
Parabola:
A parabola is the set of all points in a plane that are
equidistant from a fixed line and a fixed point (not on the line) in the plane.
The fixed line is called the directrix of the parabola
and the fixed point F is called the focus. A line
through the focus and perpendicular to the directrix is
called the axis of the parabola. The point of intersection of parabola with the
axis is called the vertex of the parabola.
Standard
equation of a parabola:
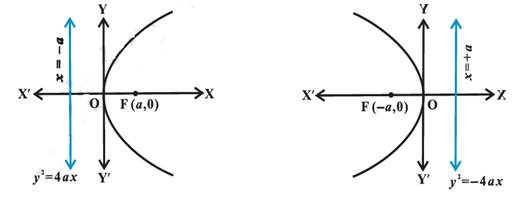
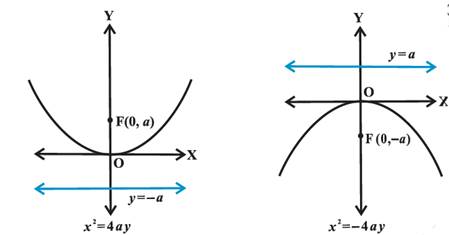
Length of latus rectum = 4a
Question 2: Find the coordinates of the focus, axis of the parabola, the
equation of the directrix and the length of the latus
rectum, ![]() .
.
Solution:
The given equation of
parabola is ![]() which is of the form
which is of the form ![]()
4a=20
a=5
Therefore, coordinates of focus
are (5,0)
Axis of parabola is y=0
Equation of directrix
is x=-5
i.e., x+5=0
Length of latus rectum=4x5=20
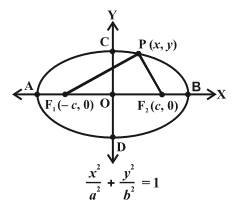
Ellipse:
An
ellipse is the set of all points in a plane, the sum of whose distances
from two fixed points in the plane is a constant.
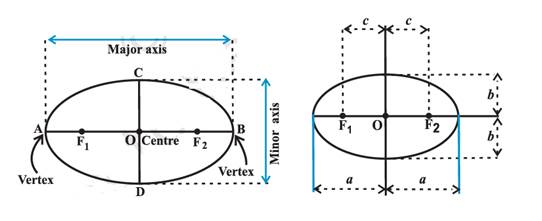
ü The two fixed points ![]() and
and ![]() are called foci (plural of
focus)
are called foci (plural of
focus)
ü The mid point of the line joining ![]() is called the centre of
ellipse.
is called the centre of
ellipse.
ü The line segment through the two foci and terminating at the
boundary of the ellipse on both sides is called major axis.
ü The line segment through the centre of the ellipse, perpendicular
to the line segment ![]() joining the two foci and
terminating at the boundary of the ellipse on both sides is called minor axis.
joining the two foci and
terminating at the boundary of the ellipse on both sides is called minor axis.
ü The ends of major-axis are called vertices of the vertices of the
ellipse.
ü The length AB of the major axis is denoted by 2a and the length of
the minor axis denoted by 2b.
ü Semi-major axis = a.
ü Semi-minor axis=b.
ü The distance between two foci ![]() and
and ![]() is 2c.
is 2c.
Relation between semi-major
axis (a), semi-minor axis (b) and the distance between the centre of the
ellipse and one of the two foci (c):
![]()
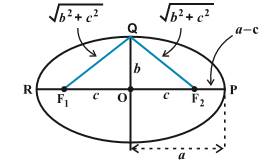
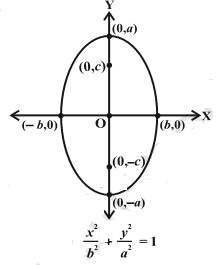
Standard equation of an
ellipse:
Latus rectum of an
ellipse: ![]()
Eccentricity: ![]()
Question 3: Find the
coordinates of the foci, the vertices, the length of major axis, the minor
axis, the eccentricity and the length of the latus rectum of the ellipse.
![]()
Solution:
The equation of given ellipse is ![]() .
.
Now, 36<9
![]() and
and ![]()
So the equation of ellipse in standard form
is ![]()
Therefore, a=6 and b=3
We know that
![]()
c =![]()
Coordinates of foci are (0,![]() ) i.e., (0,
) i.e., (0,![]() 3
3![]() )
)
Coordinates of vertices are (0,![]() a) i.e., (0,
a) i.e., (0,![]() 6)
6)
Length of major axis = 2a = 2x6 = 12
Length of minor axis = 2b = 2x3 = 6
Eccentricity (e) =![]()
Length of latus rectum = ![]()
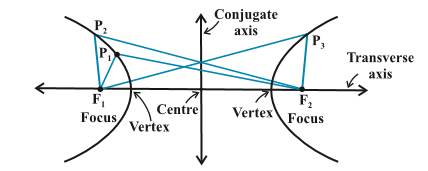
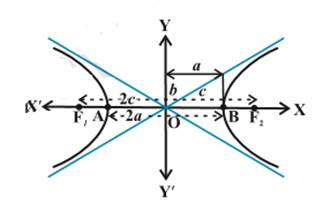
Hyperbola:
A hyperbola is the set of all points in a plane, the difference of
whose distances from two fixed points in the plane is a constant.
ü
The two
fixed points ![]() and
and ![]() are called the foci of the
hyperbola.
are called the foci of the
hyperbola.
ü
The
mid-point of the line segment ![]() joining the two foci is
called the centre of the hyperbola.
joining the two foci is
called the centre of the hyperbola.
ü
The line
through the foci ![]() and
and ![]() is called the transverse
axis of the hyperbola.
is called the transverse
axis of the hyperbola.
ü
The line
through the centre and perpendicular to the transverse axis is called the
conjugate axis.
ü
The
points at which the transverse axis meets the hyperbola are called vertices of
the hyperbola.
ü
The
distance between the two foci, i.e., ![]() is taken as 2c.
is taken as 2c.
ü
The
distance AB between the two vertices is taken as 2a.
ü
‘b’ is given by ![]() and the length conjugate axis = 2b.
and the length conjugate axis = 2b.
Focal distance of a point: The
distance of any point on the hyperbola from a focus is called the focal
distance of that point.
Eccentricity: ![]()
Standard equation of a
hyperbola:
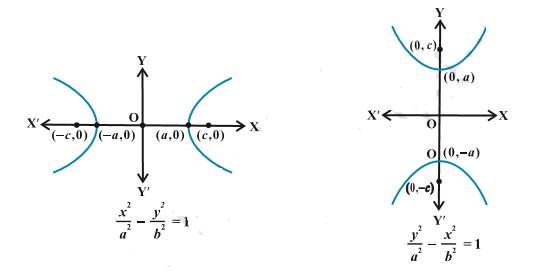
Latus rectum of a hyperbola: ![]()
Question 4: Find the
coordinates of foci and the vertices, the eccentricity and the length of the
latus rectum of the hyperbola
![]()
Solution: The equation of given hyperbola is ![]() which is of the form
which is of the form ![]() The foci and vertices of the hyperbola lie on x-axis.
The foci and vertices of the hyperbola lie on x-axis.
![]() i.e., a=5
i.e., a=5
![]() i.e., b=4
i.e., b=4
Now, by ![]()
![]()
c=![]()
Therefore, coordinates of foci are (![]() c,0) i.e., (
c,0) i.e., (![]() , 0)
, 0)
Coordinates of vertices are (![]() a, 0) i.e., (
a, 0) i.e., (![]() , 0)
, 0)
Eccentricity (e)=![]()
Length of the latus rectum = ![]() =
= ![]()