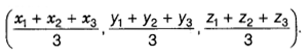Introduction to Three-dimensional
Geometry
3D Geometry
To
locate position of a object
in a line, you just need the distance of the object from the point of
reference.
To
locate the position of a point in a plane, we need two intersecting mutually
perpendicular lines in the plane. These lines are called the coordinate axes
and the two numbers are called the coordinates of the point with respect to the
axes.
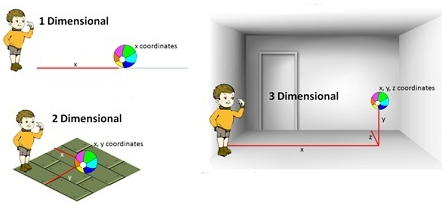
In
actual life, we do not have to deal with points lying in a line or plane only.
For
example, consider the position of a ball thrown in space at different points of
time or the position of an aero plane as it flies from one place to another at
different times during its flight.
If we
were to locate the position of a ball thrown in the room (in the air) , we will not only re quire the perpendicular
distances of the point to be located from two perpendicular walls of the room
but also the height of the point from the floor of the room. Therefore, we need
not only two but three numbers representing the perpendicular distances of the
point from three mutually perpendicular planes, namely the floor of the room
and two adjacent walls of the room. The three numbers representing the three
distances are called the coordinates of the point with reference to the three
coordinate planes. So, a point in space has three coordinates.
Coordinate Axes
In three dimensions, the coordinate axes of a rectangular cartesian
coordinate system are three mutually perpendicular lines. These axes are called
the X, Y and Z axes.
Coordinate Planes
The three planes determined by the pair of axes are
the coordinate planes. These planes are called XY, YZ and ZX plane and they
divide the space into eight regions known as octants.
Coordinates of a Point in Space
The coordinates of a point in the space are the
perpendicular distances from P on three mutually perpendicular coordinate
planes YZ, ZX, and XY respectively. The coordinates of a point P are written in
the form of triplet like (x, y, z).
The coordinates of any point on
·
X-axis is of the form (x, 0,0)
·
Y-axis is of the form (0, y, 0)
·
Z-axis is of the form (0, 0, z)
·
XY-plane are of the form (x, y, 0)
·
YZ-plane is of the form (0, y, z)
·
ZX-plane are of the form (x, 0, z)
Distance Formula
The distance between two points P(x1, y1, z1)
and Q(x2, y2, z2) is given by
![]()
The distance of a point P(x, y, z) from the origin O(0, 0, 0) is given by
OP = ![]()
Section Formula
The coordinates of the point R which divides the line segment joining two
points P(x1, y1, z1) and Q(x2, y2,
z2) internally or externally in the ratio m : n are given by
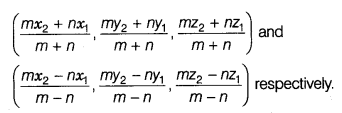
The coordinates of the mid-point of the line
segment joining two points P(x1, y1, z1) and
Q(x2, y2, z2) are
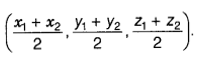
The coordinates of the centroid of the triangle,
whose vertices are (x1, y1, z1), (x2,
y2, z2) and (x3, y3, z3)
are