Linear Inequalities

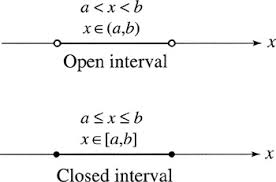
· Let a and b be two given linear variables such that a < b. Then the set of all real numbers x such that a ≤ x ≤ b is called a closed interval and is denoted by [a, b].

· Let a and b be two given linear variables such that a < b. Then the set of all real numbers x such that a < x < b is called an open interval and is denoted by (a, b).

· A statement involving variable(s) and the sign of inequality <, >, ≤ or ≥ is called an inequation or inequality.

· Let ‘a’ be a non-zero real number and x be a variable. Then inequations of the form ax + b < 0, ax + b ≤ 0, ax + b > 0 and ax + b ≥ 0 are known as linear inequations in one variable x.

· Let ‘a’, ‘b’ be non-zero real numbers and x, y be variables. Then inequations of the form ax + by < c, ax + by ≤ c, ax + by > c and ax + by ≥ c are known as linear inequations in two variables x and y.

· A solution of an inequation is the value(s) of the variable(s) that makes it a true statement.

Solving linear inequations in one variable:

Ø Some variables may be added (or subtracted) from both sides of an inequation without changing the sign of inequality.

Ø Both sides of an inequation can be multiplied or divided by the same positive real number without changing the sign of inequality. However, the sign of inequality is reversed when both sides of an inequation are multiplied or divided by a negative number.

Ø Any term of an inequation may be taken to the other side with its sign changed without affecting the sign of inequality.

Algorithm to solve a linear inequation in one variable:

Ø Obtain the linear inequation.

Ø Collect all terms involving the variable on one side of the inequation and the constant terms on the other side.

Ø Simplify both the sides of inequality in their simplest forms to reduce the inequation in the form ax < b or ax ≤ b, or ax > b, or ax ≥ b.

Ø Now, try to solve the inequation obtained in the previous step by dividing both sides of the inequation by the coefficient of the variable.

Ø Write the solution set obtained in the previous step in the form of an interval on the real line.

Equations of the form

can be solved using the following algorithm:

· Step 1: Obtain the inequation.

· Step 2: Transpose all terms on left hand side.

· Step 3: Simplify the L.H.S of the inequation obtained in the previous step to obtain an inequation of the form

· Step 4: Make the coefficients of numerator and denominator as positive (in case they are not).

· Step 5: Equate the numerator and denominator separately to zero and obtain the values of x. These values of x are also termed as critical points.

· Step 6: Now, plot the critical points obtained in the previous step on real line. These points will divide the real line in three regions.

· Step 7: In the right most region, the expression on L.H.S. of the inequation obtained in step 4 will be positive while in other regions it will be alternatively negative and positive. So first of all, mark a positive sign in the rightmost region and then mark and then mark alternative negative and positive signs in the other regions.

· Step 8: Select appropriate region on the basis of the sign of the inequation obtained in step 4. These regions should be written in the form of intervals in order to obtain the desired solution sets of the given inequation.

Algorithm to solve a system of linear inequations in one variable:

Ø Obtain the system of linear inequations.

Ø Solve each inequation and obtain their solution sets. Then, represent them on real line as well.

Ø Find the intersection of the solution sets obtained in the previous step by taking the help of the graphical representation of the solution sets of the last step.

Ø The set obtained in the last step is the required solution set of the given system of inequations.

Some important results:

· If a is a positive real number, then

|x| < a ⇔ -a < x < a i.e. x ∈ (-a, a).

|x| ≤ a ⇔ -a ≤ x ≤ a i.e. x ∈ [-a, a].

|x| > a ⇔ x < -a or x > a

|x| ≥ a ⇔ x ≤ -a or x ≥ a

· Let r be a positive real number and a be a fixed real number. Then,

          |x – a| < r ⇔ a – r < x < a + r i.e. x ∈ (a - r, a + r).

          |x – a| ≤ r ⇔ a – r ≤ x ≤ a + r i.e. x ∈ [a – r, a + r].

          |x – a| > r ⇔ x < a - r  or x > a + r

          |x – a| ≥ r ⇔ x ≤ a - r or x ≥ a + r

· Let a and b be positive real numbers .Then

· a < |x| < b ⇔ x ∈ (-b, -a) ∪ (a, b)

· a ≤ |x| ≤ b ⇔ x ∈ [-b, -a] ∪ [a, b]

· a ≤ |x-c| ≤ b ⇔ x ∈ [-b+c, -a+c] ∪ [a+c, b+c]

· a < |x-c| < b ⇔ x ∈ (-b+c, -a+c) ∪ (a+c, b+c)

Graphical solution of linear inequations in two variables:

Ø Convert the given inequation, say ax + by ≤ c, into the equation ax + by = c which represents a straight line in xy-plane.

Ø Put y = 0 in the equation obtained in the previous step to get the point where the line meets with x-axis. Similarly, put x = 0 to obtain a point where the line meets y -axis.

Ø Join the points obtained in the previous step to obtain the graph of the line obtained from the given inequation. In case of a strict inequality, i.e. ax + by < c or ax + by > c, draw the dotted line, or mark it with a thick line.

Ø Choose a point, if possible (0, 0), not lying on this line. Substitute the coordinates in the inequation. If the inequation is satisfied, then shade the portion of the plane which contains the chosen point. Else, shade the portion which does not contain the chosen point.

Ø The shaded region obtained in the previous step represents the desired solution set.