Mathematical
Reasoning
Logic
Logic is the subject that deals with
the method of reasoning. It provides us rules for determining the validity of a
given argument in proving theorem.
Statement (Proposition)
A statement is an assertive sentence
which is either true or false but not both a true statement is called valid
statement. Otherwise it is called invalid statement. Statements are denoted by
the small letters
i.e.,
p, q, r … etc.
Open and Compound Statement
A sentence which contains one or more
variable such that when certain values are given to the variable it becomes a
statement, is called an open statement.
If two or more simple statements are
combined by the use of words such as ‘and’, ‘or’, ‘not’, ‘if’, ‘then’, ‘if and
only if ‘, then the resulting statement is called a compound statement.
Truth Value and Truth Table
A statement can be either ‘true’ or
‘false’ which are called truth values of a .statement and it is represented by
the symbols T and F, respectively.
A.
truth table is a summary of truth values of the resulting statements for all
possible assignment of values to the variables appearing in a compound
statement.
Number
of rows depends on their number of statements.
Truth Table for Two Statements (p, q)
Number
of rows = 22 = 4
|
p |
q |
|
T |
T |
|
T |
F |
|
F |
T |
|
F |
F |
Elementary Operation of Logic
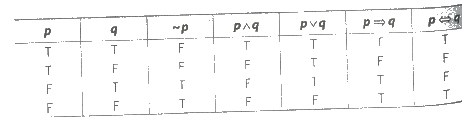
(i) Conjunction A compound sentence formed by
two simple sentences p and q using connective ‘and’ is called the conjunction
of p and q and it is represented by p ∧ q.
(ii) Disjunction A
compound sentence formed by two simple sentences p and q using connectives ‘or’
is called the disjunction of p and q and it is represented by p ∨
q.
(iii) Negation A statement which is formed by
changing the truth value of a given statement by using the word like ‘no’,
‘not’ is called negation of given statement. If p is a statement, then negation
of p is denoted by ~ p.
(iv) Conditional
Sentence (Implication) Two simple sentences p and q
connected by the phase, if and then, is called conditional sentence of p and q
arid it is denoted by p => q.
(v) Biconditional Sentence (Bi-implication) The two simple sentences connected by
the phrase, ‘if and only if this is called biconditional
sentences. It is denoted by the symbol ‘<=>’.
Table for Basic Logical Connections
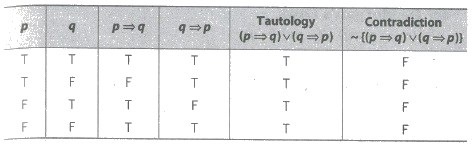
Tautology and Contradiction
The compound statement which are true
for every value of their components are called tautology.
The compound statements which are
false for every value of their components are called contradiction (fallacy).
Truth Table
Quantifiers and Quantified Statements
In
this statements, there are two important symbols are used.
(i) The
symbol ‘∀’ stands for ‘all values of ‘.
This is known as universal quantifier.
(ii) The symbol ‘∃’
stands for ‘there exists’.
The symbol ∃
is known as existential quantifier.
Quantified Statement
An open sentence with a quantifier
becomes a statement, called a quantified statement.
Negation of a Quantified Statement
(i) ~{∀ x ∈ A : p(x) is true} = {∃
x ∈
A such that (s.t.) ~ p(x) is true}
(ii) ~{∃x
∈
A : p(x) is true} = {∀ x ∈ A : ~ p(x) is true}
Laws of Algebra of Statements
(i) Idempotent Laws
(a) p ∨
p ≡ p
(b) p ∧
p ≡ p
(ii) Associative
Laws
(a) (p ∨
q) ∨
r ≡ p ∨ (q ∨ r)
(b) (p ∧
q) ∧
r ≡ p ∧ (q ∧ r)
(iii) Commutative
Laws
(a) p ∨
q ≡ q ∨ p
(b) p ∧
q ≡ q ∧ P
(iv) Distributive
Laws
(a) p ∨
(q A r) ≡ (p ∨ q) ∧ (p ∨ r)
(b) p ∧
(q ∨
r) ≡ (p ∧ q) ∨ (p ∧ r)
(v) De
Morgan’s Laws
(a) ~(p ∨
q) ≡ (~ p) ∧ (,_ q)
(b) ~(p ∧
q) ≡ (~ p) ∨ (~ q)
(vi) Identity
Laws
(a) p ∧
F ≡ F
(b) p ∧
T ≡ p
(c) p ∨
T ≡ T
(d) p ∨
F ≡ p
(vii) Complement
Laws
(a) p ∨
(~ p) ≡ T
(b) p ∧
(~ p) ≡ F
(c) ~ (~p) ≡ p
(d) ~ T ≡ F, ~ F ≡ T
Important Points to be remembered
(i) The number of rows of table is depend on the number of
statements.
(a) If p is false, then ~ p is true.
(b) If P is true, then ~ p is false.
(ii)
(a) The
converse of p => q is q => p.
(b) The inverse of p => q is ~ p
=> ~ q.
(iii)
The contrapositive of p => q is ~ q => ~ p.
A
statement which is neither a tautology nor a contradiction is a contingency.