Probability
Introduction:
Probability is a measure of uncertainty
of various phenomenon. This is the most important concept in modern science.. The interpretation of the word probability involves
synonyms such as chance, odds, uncertainty, prevalence, risk, expectancy etc.
“We use
probability when we want to make an affirmation, but are not quite sure” writes
J. R. Lucas.
To
understand the approaches of probability, we have to know some basic topics
like random experiment, sample space, events etc.
Random experiment:
A random experiment is an experiment
whose outcomes can’t be predict.
However in most cases the collection of
every possible outcome of a random experiment can be listed.
Outcomes:
A possible result of a random
experiment is called its outcome.
Sample space:
A sample space of a random experiment
is the collection of all possible outcomes.
Each element of sample space is called
sample point.
Sample space is denoted by S.
Example 1: What is the sample space if one coin is
tossed once?
Solution: Since either a coin turn up head (H)
or tail (T). Then sample space is ![]()
Example 2: Describe a sample space of rolling a
die.
Solution: The sample space of this experiment is ![]()
Exercise 16.1
In each of
the following experience 1 to 7, describe the sample space for the indicated
experiment.
1.
A
coin is tossed three times.
Solution:
Since either a coin turn up head (H) or tail (T). Then sample space is
![]()
2.
A
die is thrown 2 times.
Solution: Since
a die has six face ![]() , then If a die is thrown two times
then the sample space will be
, then If a die is thrown two times
then the sample space will be
![]()
![]()
![]()
![]()
![]()
![]()
3.
A
coin is tossed four times.
Solution: If a coin is tossed 1 time
the sample space is ![]()
Then the sample space of tossing one
coin four times is given by
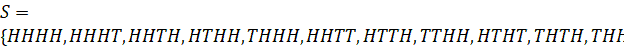
![]()
![]()
In the 1st toss we get one
head (H) and one tail (T), shown in the picture.
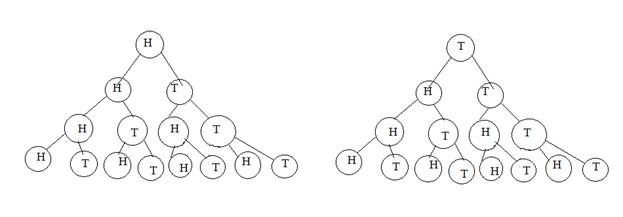
4.
One
coin is tossed and one die is thrown.
Solution: The sample space of throwing one coin once is ![]() and that of one die is
and that of one die is ![]() .
.
Hence the required sample space is
given by
![]()
Events of a sample space:
An event is a set of outcomes of an experiment
to which a probability is assigned. That is a subset of the sample space.
Occurrence of an event:
In any given experiment or trial, there
is a probability that either an event occurs or it does not. The probability of
the occurrence of an event lies between 0 and 1.
Types of events:
Simple event:
An event is called simple event the
sample space contain only one sample point.
Example: If a die is thrown then the possibility
of appearing 6 is a simple event. And is given by ![]() .
.
Compound event:
An event is called compound event if
the sample space contain more than one sample point.
Example: If a die is thrown then the possibility
of odd number appearing is compound event because there are three
possibilities, i.e., ![]()
Certain event:
An event is called certain event which
is sure to occur in any experiment.
The whole sample space is called sure
event.
Impossible event:
An event is called impossible event if
there is no chance to occurring of an event. ![]() is called impossible event.
is called impossible event.
Equally likely event:
The events are called equally likely
event if the outcomes of an experiment are equally likely to happen.
Example: If
a coin is tossed then the there are equally likely to
get head and tail.
Complementary event:
For any event ![]() , the non-occurrence event is called
complimentary event.
, the non-occurrence event is called
complimentary event.
Example: Let a die is thrown. Then getting an
odd face and even face are complimentary event.
Mutually exclusive event:
Two events are said to be mutually
exclusive events if both can’t occur at the same time.
In other ward, let ![]() be
be![]() be are two events of a ample space
be are two events of a ample space ![]() . Then they are said to be mutually
exclusive if
. Then they are said to be mutually
exclusive if ![]() , i.e., if they are disjoint.
, i.e., if they are disjoint.
Mutually exclusive events always have
different outcomes.
S imple events
of a sample space are always mutually exclusive.
Exhaustive events:
Let ![]() be n events of a sample space
be n events of a sample space
![]() . Then They are said to be Exhaustive
events if
. Then They are said to be Exhaustive
events if ![]() .
.
Notation of some events:
|
Description of the event |
Theoretic notation |
|
Not |
|
|
|
|
|
|
|
|
|
|
|
Neither |
|
|
At least one of |
|
|
All three of |
|
Exercise 16.2
1.
A
die is rolled. Let ![]() be the event “die shows 4” and
be the event “die shows 4” and ![]() be the event “die shows even number”. Are
be the event “die shows even number”. Are ![]() and
and ![]() are mutually exclusive?
are mutually exclusive?
Solution: Here ![]()
The event ![]() and
and ![]()
Then ![]() . Hence they are not mutually
exclusive.
. Hence they are not mutually
exclusive.
2.
A
die is thrown. Describe the following events.
Solution: If a die is thrown then the
sample events are ![]()
(i)
A:
a number less than 7
Solution: Here ![]()
(ii)
B:
a number greater than 7
Solution: Since in throwing a die there
is no number occur which is greater than 7. Then
![]() .
.
(iii)
C:
a multiple of 3
Solution: Here in ![]() only multiple of 3 are 3 and 6.
only multiple of 3 are 3 and 6.
Hence ![]()
(iv)
D:
a number less than 4.
Solution: The number less than 4 in
sample space are 1, 2, 3
Hence ![]()
(v)
E:
an even number greater than 4.
Solution: Here ![]()
(vi)
F:
a number not less than 3.
Solution: The number not less than 3
are 3, 4, 5, 6.
Hence ![]()
Now ![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Probability function:
Let ![]() be sample space associated to a random space.
And let
be sample space associated to a random space.
And let ![]() be any event. Then the function P which
assigns every
be any event. Then the function P which
assigns every ![]() to a unique non-negative real number P
to a unique non-negative real number P![]() is called probability function if it satisfies
the following axioms:
is called probability function if it satisfies
the following axioms:
(i)
![]() P
P![]()
(ii)
P![]() , i.e.,
, i.e., ![]()
(iii)
For
any event ![]() , P
, P![]() , the number P
, the number P![]() is called probability of eliminatory event
is called probability of eliminatory event ![]()
Probability
of an event:
Let ![]() be the number of
eliminatory events associated with a random experiment and
be the number of
eliminatory events associated with a random experiment and ![]() be the number of favorable cases to an event
be the number of favorable cases to an event ![]() . Then the probability of occurrence of
. Then the probability of occurrence of
![]() is denoted by P
is denoted by P![]() and is defined by P
and is defined by P![]()
Some Proves of related
results:
1.
![]() P
P![]()
Proof: We know that if ![]() be the number of eliminatory events associated
with a random experiment and
be the number of eliminatory events associated
with a random experiment and ![]() be the number of favorable cases to an event
be the number of favorable cases to an event ![]() . Then the probability of occurrence of
. Then the probability of occurrence of
![]() is denoted by P
is denoted by P![]() and is defined by P
and is defined by P![]()
Now, since ![]()
Implies ![]()
Implies ![]() P
P![]() (proved)
(proved)
2.
![]()
Proof: Let ![]() be the number of eliminatory events associated
with a random experiment and
be the number of eliminatory events associated
with a random experiment and ![]() be the number of favorable cases to an event
be the number of favorable cases to an event ![]() . If
. If ![]() be the complement of the event
be the complement of the event ![]() then occurrence of
then occurrence of ![]() is
is ![]()
Therefore ![]()
![]()
![]()
i.e., ![]()
Theorem 1: (Addition theorem for two events) If ![]() and
and ![]() are two events associated with a random
experiment, Then
are two events associated with a random
experiment, Then ![]() .
.
Proof: 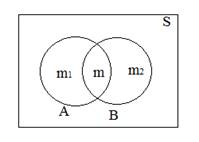
Let ![]() be the sample space associated with the random
experiment experiment. Also let
be the sample space associated with the random
experiment experiment. Also let ![]() contains
contains ![]() mutually exclusive events and
mutually exclusive events and ![]() be the number of eliminatory events favorable
to
be the number of eliminatory events favorable
to ![]() and
and![]() respectively.
respectively.
Then
![]() ,
, ![]() and
and ![]()
Now the
number of events favorable to ![]() only is
only is ![]() , favourable to
, favourable to ![]() only is
only is ![]() and then favourable to
and then favourable to ![]() or
or![]() i.e.,
i.e.,
Number of events favorable to ![]() is number of events favorable to
is number of events favorable to ![]() number of events favorable to
number of events favorable to ![]() number of events favorable to
number of events favorable to
![]() .
.
i.e.,
number of events favorable to ![]()
Hence ![]()
i.e., ![]()
i.e., ![]() (proved)
(proved)
Theorem 2: (Addition theorem for three events) Let ![]() are three events associated with a random experiment. Then
are three events associated with a random experiment. Then
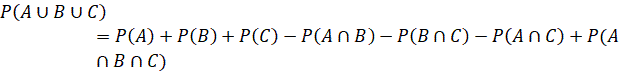
Proof: Let
![]()
Then ![]()
Putting ![]() in the above equation,
in the above equation,
![]()
![]()
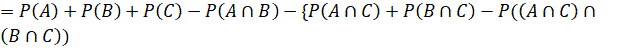
![]()
Corollary:
If ![]() are mutually exclusive events, then
are mutually exclusive events, then
![]() .
.
Hence ![]()
And ![]()
Theorem: For any two events ![]() and
and ![]() ,
, ![]()
Proof:
Since ![]() then
then ![]()
Also ![]() the
the ![]()
Since we
know that, ![]()
Hence ![]()
Combining
(1), (2) and (3) we get,
![]() (Proved)
(Proved)
Some related properties
of Probability:
(i)
![]()
(ii) ![]()
(iii) ![]()
(iv) ![]()
Example: ![]() and
and ![]() are two events such that
are two events such that ![]() and
and ![]() . Find
. Find
(i)
![]()
(ii)
![]()
(iii)
![]()
(iv)
![]()
Solution:
(i)
![]()
![]()
![]()
(ii)
![]()
![]()
![]()
(iii)
![]()
![]()
(iv)
![]()
![]()