Functions

Exercises Problems

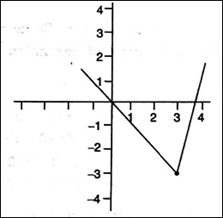
1) Find the domain and range of f(x) = |2x - 3| - 3

Solution:

Given, f(x) = |2x - 3| - 3.

The domain of the expression in all real number except where the expression in undefined. In this case, there is not real number that makes the expression undefined

Therefore,

Domain of f = (- ?, ?) = R

The absolute value of expression has a ‘V’ shape. The range of a positive absolute value expression starts at its vertex and extends to infinity.

Range of f = (- 3, ꚙ) or {y/y ≥ - 3}

2) Draw the graph of the Greatest Integer Function.

Solution:

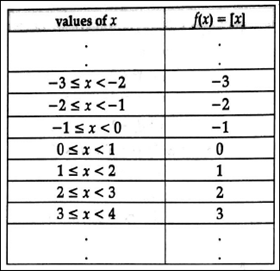The greatest integer function is denoted by y = [x]. For all real numbers, x, the greatest integer function returns the largest integer less than or equal to x.

3) Draw the graph of constant function f: R → R; f(x) = 2Ɐ x ϵ R. Also, find its domain and range.

Solution:

Given, f: R → R; f(x) = 2Ɐ x ϵ R

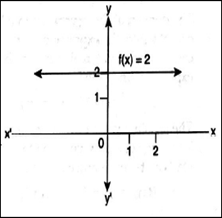
Domain = R and range = {2}

4) Find the domain and range of the following real function : f(x) =

Solution:

Given, f(x) =

Domain:

We know that f(x) is defined when x – 2 ≠ 0

i.e., x ≠ 2

Therefore, The domain is all values of x that makes the expression defined i.e.,

Domain of f = R – (2)

Range:

Let y = f(x)

Therefore y =

Y(x – 2) = x + 1

X(y – 1) = 2y + 1

x =

Since, x is defined, when y – 1 ≠ 0 i.e., y ≠ 1

Therefore, Range of f = R – {1}.

5) Find the domain and range of the following real function : f(x) =

Solution:

Given, f(x) =

Domain: Clearly, f(x) is defined for all x ← R except x = 1

Therefore, Domain of f = R – {1}

Range:

Now, f(x) = = 1, when x > 1

And f(x) = = - 1, when x < 1

Therefore, Range of f = {-1, 1}

6) Find the domain and range of the following real function : f(x) =

Solution.

Given, f(x) =

Domain: Clearly, f(x) is defined for all x ϵ R expect x = 3

Therefore, Domain of f = R – {3} = (- ꚙ, 3), ꓴ (3, ꚙ)

Range:

Let y = f(x)

Therefore, y =

ð y = x + 3

It follows from the above relation that y takes all real values except 6 when x takes values in the set R – {3}

Therefore, Range of f = R – {6}

7) Find the domain and range of the following real function : f(x) =

Solution:

Given, f(x) =

Domain: Clearly, f(x) is defined for all x ϵ R except x = 4

Therefore, Domain of f = R – {4} = (- ꚙ, 4), U (4, ꚙ)

Range:

Let y = f(x)

ð y =

ð y = = - 1

ð Therefore, Range of f = {- 1}

8) Find the domain and range of the following real function : f(x) = 1 - |x - 3|

Solution:

Given, f(x) = 1 - |x - 3|

Domain: We observe that f(x) is defined for all x ϵ R

Therefore, Domain of f = R

Range: Now,

0 ≤ |x - 3| < ꚙ Ɐ x ϵ R

ð - ꚙ < - |x - 3| ≤ 0 Ɐ x ϵ R

ð - ꚙ < 1 - |Ɐ - 3| ≤ 1 Ɐ x ϵ R

ð - ꚙ < f(x) ≤ 1 Ɐ x ϵ R

Hence, Range of f = (- ꚙ, 1)

9) Determine a quadratic function (f) is defined by f(x) = ax² + bx + c. If f(0) = 6, f(2) = 1, f(-3) = 6.

Solution:

Given, f(x) = ax² + bx + c.

At x = 0, f (0) = 6(given)

Therefore, a x 0 + b x 0 + c = 6

Therefore, c= 6 …. (i)

At x = 2, f (2) = 1(given)

Therefore, a (2)² + b (2) + c = 1

ð 4a + 2b + 6 = 1 (using(i))

ð 4a + 2b = - 5 (ii)

At x = - 3, f (-3) = 6

Therefore, a (-3)² + b (-3) + c = 6

ð 9a – 3b + 6 = 6 (using(i))

ð 9a – 3b = 0 ….(iii)

On solving eqs. (ii) And (iii), we get

a = - and a = -

Therefore, required quadratic function (f) = x² + x + 6

10) If [x] denotes the greatest integer function. Find the solution set of equation.[x]² - 5[x] + 6 = 0

Solution:

Given, equation, [x]² - 5[x] +6 = 0

[x]² - 3[x] – 2[x] + 6 = 0

[x]([x] – 3) – 2([x] – 3) = 0

([x] – 3) ([x] – 2) = 0

[x] = 2 or [x] = 3

2 ≤ x < 3 or 3 ≤ x < 4

Hence, x ϵ [2, 4]