Relations

Exercises Problems:

1) Let A = {1,2,3,4}, B = {1,4,9,16,25} and R be a relation defined from A to B as,

R = {(x,y) : x ϵ A, y ϵ B and y = x²}

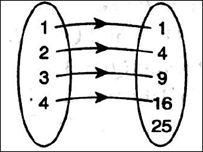
i) Depict this relation using arrow diagram

ii) Find domain of R

iii) Find range of R

iv) Write co-domain of R

Solution:

Given, A = {1, 2, 3, 4} and B = {1, 4, 9, 16, 25} and R = {(x, y): x ϵ A, y ϵ B and y = x²}

i) Relation R = {(1,1), (2,4), (3,9), (4,16)}

ii) Domain of R = {1,2,3,4}

iii) Range of R = {1,4,9,16}

iv) Co-domain of R = {1, 4, 9, 16, 25}.

2) If A = {2,4,6,9} B = {4,6,18,27,54} and a relation R from A to B is defined by R = {(a,b) : a ϵ A, b ϵ B a is a factor of b and a < b}, then find in Roster form. Also find its domain and range.

Solution:

A = {2, 4, 6, 9} B = {4, 6, 18, 27, 54} and R = {(a, b): a ϵ A, b ϵ B a is a factor of b and a < b}

Roster form, R = {(2, 4), (2, 6), (2, 18), (2, 54), (6, 18), (6, 54), (9, 18), (9, 27), (9, 54}

Domain of R = {2, 6, 9}

Range of R = {4, 6, 18, 27, 54}

3) Let A = {2, 3, 4, 5, 6, 7, 8, 9}. Let R be the relation on A defined by {(x,y) : x,y ϵ A, x is a multiple of y and x ≠ y

i) Find the relation.

ii) Find the domain of R

iii) Find the range of R

iv) Find the inverse relation

Solution:

i) R = {(4,2), (6,2), (8,2), (6,3), (9,3), (8,4)}

ii) Domain of R = {4,6,8,9}

iii) Range of R = {2,3,4}

iv) R⁻¹ = = {(2,4), (2,6), (2,8), (3,6), (3,9), (4,8)}

4) Define a relation R on the set N of natural numbers by R = {(x,y) : y = 2x – 1; x,y ϵ N, x ≤ 5}. Depict this relationship using roster form. Write down the domain and range.

Solution:

Given y = 2x -1 and x ≤ 5

For x = 1, y = 2 x 1 – 1 = 1

x= 2, y = 2 x 2 – 1 = 3

x= 3, y = 2 x 3 – 1 = 5

x = 4, y = 2 x 4 – 1 = 7

x = 5, y = 2 x 5 – 1 = 9

Relation R = {(1, 1), (2, 3), (3, 5), (4, 7), (5, 9)}

Domain = {1, 2, 3, 4, 5}

Range = {1, 3, 5, 7, 9}

5) Let A = {1, 2, 3}, B = {3, 4} and C = {4, 5, 6}. Find,

i) A x (B Ո C)

ii) (A x B) Ո (A x C)

Solution:

i) A x (B Ո C)

= {1, 2, 3} x {4}

= {(1, 4), (2, 4), (3, 4)}

ii) (A x B) Ո (A x C)

= ({1, 2, 3} x {3, 4}) Ո ({1, 2, 3} x {4, 5, 6})

= {(1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3,4)} Ո {(1,4), (1,5), (1,6), (2,4), (2,5), (2,6), (3,4), (3,5), (3,6)}

= {(1, 4), (2,4), (3,4)}