Sets

Definition of Set

Set is a collection of well defined objects which are distinct from each other. Sets are usually denoted by capital letters A,B,C,… and elements are usually denoted by small letters a,b,c,…

If ‘a’ is an element of a set A, then we write a ∈ A and say ‘a’ belongs to A or ‘a’ is in A or ‘a’ is a member of A. If ‘a’ does not belong to A, we write a ∉ A.

Standard Set Notations

• N : A set of natural numbers.

• W : A set of whole numbers.

• Z : A set of integers.

• Z⁺/Z^- : A set of all positive/negative integers.

• Q : A set of all rational numbers.

• Q⁺/Q^- : A set of all positive/ negative rational numbers.

• R : A set of real numbers.

• R⁺/R^-: A set of all positive/negative real numbers.

• C : A set of all complex numbers.

Methods for Describing a Set

Roster/Listing Method/Tabular Form

In this method, a set is described by listing elements, separated by commas, within braces. e.g., A = {a, e, i, o, u}

Set Builder/Rule Method

In this method, we write down a property or rule which gives us all the elements of the set by that rule. e.g., A = {x : x is a vowel of English alphabets}

Types of Sets

Finite Set

A set, containing finite number of elements or no element, is called finite set.

Cardinal Number of a Finite Set

The number of elements in a given finite set is called cardinal number of finite set, denoted by n(A).

Infinite Set

A set containing infinite number of elements is called infinite set.

Empty/Null/Void Set

A set containing no element, it is denoted by Φ or { }.

Singleton Set

A set containing a single element, is called singleton set.

Equal Sets

Two sets A and B are said to be equal, if every element of A is a member of B and every element of B is a member of A and we write A = B.

Equivalent Sets

Two sets are said to be equivalent, if they have same number of elements.

If n(A) = n(B), then A and B are equivalent sets. But converse is not necessarily true.

Subset and Superset

Let A and B be two sets. If every element of A is an element of B, then A is called subset of B and B is called superset of A. Written as

A ⊆ B or B ⊇ A

Proper Subset

If A is a subset of B and A ≠ B, then A is called proper subset of B and we write A ⊂ B.

Universal Set (U)

A set consisting all possible elements which occurs under consideration is called a universal set.

Comparable Sets

Two sets A and B are comparable, if A ⊆ B or B ⊆ A.

Non-Comparable Sets

For two sets A and B, if neither A ⊆ B nor B ⊆ A, then A and B are called non-comparable sets.

Power Set (P)

The set formed by all the subsets of a given set A, is called power set of A, denoted by P(A). If n(A) = m then n(P(A)) = 2^m.

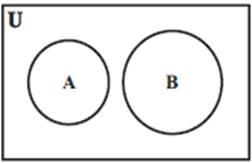
Disjoint Sets

Two sets A and B are called disjoint, if, A ∩ B = (Φ).

Intervals as subsets of R

Open Interval

Let a, b ∈ R and a < b. Then the set of real numbers { y : a < y < b} is called an open interval and is denoted by (a, b). All the points between a and b belong to the open interval (a, b) but a, b themselves do not belong to this interval.

Closed Interval

The interval which contains the end points also is called closed interval and is denoted by [a, b ].

[a, b ] = {x : a ≤ x ≤ b}

• Intervals can be closed at one end and open at the other, i.e.,

[a, b) = {x : a ≤ x < b} is an open interval from a to b, including a but excluding b.

(a, b ] = { x : a < x ≤ b } is an open interval from a to b including b but excluding a.

• The set [0, ∞) defines the set of non-negative real numbers, while set (– ∞, 0) defines the set of negative real numbers. The set (– ∞, ∞) describes the set of real numbers in relation to a line extending from – ∞ to ∞.

On real number line, various types of intervals described above as subsets of R,

Venn Diagram

In a Venn diagram, the universal set is represented by a rectangular region and a set is represented by circle or a closed geometrical figure inside the universal set

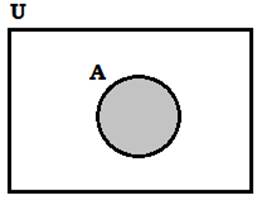
Operations on Sets

Union of Sets

The union of two sets A and B, denoted by A ∪ B is the set of all those elements, each one of which is either in A or in B or both in A and B.

A ∪ B = { x : x ∈ A or x ∈ B }

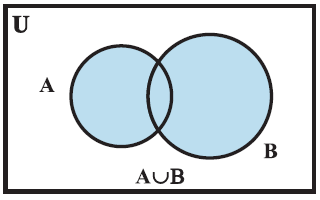
Some Properties of the Operation of Union

a. A ∪ B = B ∪ A (Commutative law)

b. (A ∪ B) ∪ C = A ∪ (B ∪ C) (Associative law)

c. A ∪ Φ = A (Law of identity element, Φ is the identity of ∪)

d. A ∪ A = A (Idempotent law)

e. U ∪ A = U (Law of U)

Intersection of Sets

The intersection of two sets A and B, denoted by A∩B, is the set of all those elements which are common to both A and B.

A ∩ B = {x : x ∈ A & x ∈ B}

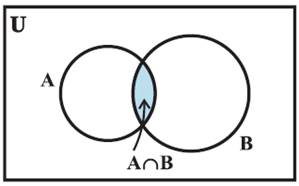
If A and B are two sets such that A∩B = Φ, then A and B are called disjoint sets.

Some Properties of Operation of Intersection

f. A ∩ B = B ∩ A (Commutative law).

o (A ∩ B) ∩ C = A ∩ (B ∩ C) (Associative law).

o Φ ∩ A = Φ,

U ∩ A = A (Law of Φ and U).

o A ∩ A = A (Idempotent law).

o A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C), i. e., ∩ distributes over ∪, and

A ∩ (B ∪ C) = (A ∪ B) ∩ (A ∪ C), i. e., ∪ distributes over ∩

(Distributive law)

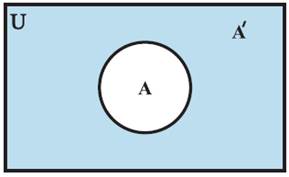
Complement of a Set

If A is a set with U as universal set, then the complement of A is the set of all elements of U which are not the elements of A. It is denoted by A’.

A′ = {x : x ∈ U and x ∉ A }. ⇒ A′ = U – A

Some Properties of Complement Sets

1. Complement laws:

(i) A ∪ A′ = U (ii) A ∩ A′ = Φ

2. De Morgan’s law:

(i) (A ∪ B)´ = A′ ∩ B′ (ii) (A ∩ B)′ = A′ ∪ B′

3. Law of double complementation: (A′)′ = A

4. Laws of empty set and universal set

Φ′ = U and U′ = Φ.

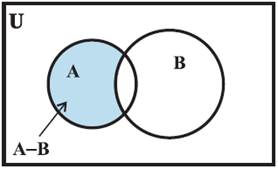
Difference of Sets

For two sets A and B, the difference A-B is the set of all those elements of A which do not belong to B.

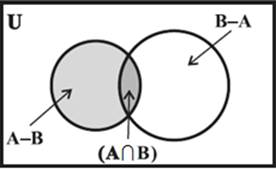
The sets A-B, A∩B and B-A are mutually disjoint sets, i.e., the intersection of any of these two sets is the null set

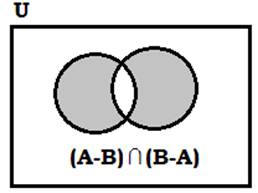
Symmetric Difference of Sets

For two sets A and B, symmetric difference is the set (A-B) ∪ (B-A) denoted by A~B.

Important Points to be Remembered About Sets

• Every set is a subset of itself i.e., A ⊆ A, for any set A.

• Empty set Φ is a subset of every set i.e., Φ ⊂ A, for any set A.

• For any set A and its universal set U, A ⊆ U

• If A = Φ, then power set has only one element i.e., n(P(A)) = 1

• Power set of any set is always a non-empty set.

• If a set A has m elements, then P(A) or power set of A has 2^m elements.

• Equal sets are always equivalent but equivalent sets may not be equal.

• The set {Φ} is not a null set. It is a set containing one element Φ.

Results on Number of Elements in Sets

• n (A∪B) = n(A) + (B) - n(A∩B)

• n(A∪B) = n(A) + n(B), if A and B are disjoint.

• n(A – B) = n(A) – n(A ∩ B)

• n(A + B) = n(A) + n(B) - 2n(A ∩ B) [Belonging to exactly one]

• n(A ∪ B ∪ C)= n(A) + n(B) + n(C) - n(A ∩ B) – n(B ∩ C) - n(A ∩ C) + n(A ∩ B ∩ C)

• n(A’ ∪ B’) = n(A ∩ B)’ = n(U) – n(A ∩ B)

• n(A’ ∩ B’) = n(A ∪ B)’ = n(U) – n(A ∪ B)

• n(B – A) = n(B) - n(A ∩ B)