Statistics
Introduction:
Statistics
deals with data collected for specific purposes. We can make decisions about
the data by analyzing and interpreting it. There are methods of finding a
representative value for the given data. This value is called the measure of
central tendency. The three measures of central tendency are mean, median and
mode.
Mean: The mean
or average of observations is the sum of the values of all the observations
divided by the total number of observations.
Median: The median is the measure of central
tendency which give us the value of the middle most observation in the data.
If n is
odd, the median is the ![]() observation.
observation.
If
n is even, the will be the average of the ![]() and the
and the ![]() observation.
observation.
Mode: A mode is that value among the
observation which occurs most often, that is, the value of the observation
having the maximum frequency.
Measures of Dispersion:
The measure of
dispersion shows the scatterings of the data. It tells the variation of the
data from one another and gives a clear idea about the distribution of the
data. The measure of dispersion shows the homogeneity or the heterogeneity of
the distribution of the observations. The following are the measures of
dispersion:
I.
Range
II.
Quartile deviation
III.
Mean Deviation
IV.
Standard deviation
Range:
It
is the difference between two extreme observations of the data set. If X max and
X min are the two extreme observations then
Range
= X max – X min
Mean Deviation:
Mean deviation is the
arithmetic mean of the absolute deviations of the observations from a measure
of central tendency. If x1, x2, … , xn are
the set of observation, then the mean deviation of x about the average A (mean,
median, or mode) is
Mean
deviation from average A =![]()
![]()
I.
Mean Deviation for Ungrouped Data:
a. M.D.(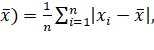 where
where ![]() =Mean
=Mean
Question 1: Find the mean deviation about the mean for the data given
38,70,48,40,42,55,63,46,54,44
Solution: Mean of the given data is
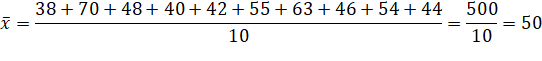
M.D.(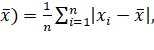 where
where ![]() =Mean
=Mean
|
|
|
|
38 70 48 40 42 55 63 46 54 44 |
12 20 2 10 8 5 13 4 4 6 |
|
Total |
84 |
M.D. about mean=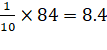
M.D.(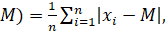 where M=Median
where M=Median
Question 2: Find the mean
deviation about median for the data given
13,17,16,14,11,13,10,16,11,18,12,17
Solution: Arrange the data in
ascending order, we have
10,11,11,12,13,13,14,16,16,17,17,18
Here, n=12(even number)
So median is average of 6th
and 7th observations
Median=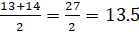
M.D.(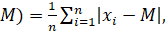 where M=Median
where M=Median
|
|
|
|
10 11 11 12 13 13 14 16 16 17 17 18 |
3.5 2.5 2.5 1.5 0.5 0.5 0.5 2.5 2.5 3.5 3.5 4.5 |
|
Total |
28 |
M.D. about median=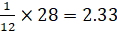
II.
Mean Deviation for Grouped Data:
a.
Discrete Frequency Distribution: A
discrete frequency distribution lists all the observed values.
![]()
![]()
i.
Mean Deviation about Mean:
M.D.(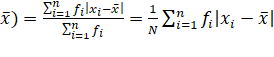
Question 3: Find the mean deviation about the mean for the data given
|
|
5 |
10 |
15 |
20 |
25 |
|
|
7 |
4 |
6 |
3 |
5 |
Solution: Mean (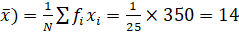
|
|
|
|
|
|
|
5 10 15 20 25 |
7 4 6 3 5 |
35 40 90 60 125 |
9 4 1 6 11 |
63 16 6 18 55 |
|
|
25 |
350 |
|
158 |
M.D. about mean 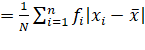
=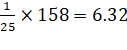
ii.
Mean Deviation about Median:
M.D.(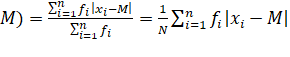
Question 4: Find the mean
deviation about median for the data given
|
|
5 |
7 |
9 |
10 |
12 |
15 |
|
|
8 |
6 |
2 |
2 |
2 |
6 |
Solution: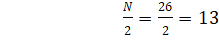
The c.f. just greater
than 13 is 14 and corresponding value of x is 7.
Therefore, Median=7
|
|
|
|
|
|
|
5 7 9 10 12 15 |
8 6 2 2 2 6 |
8 14 16 18 20 26 |
2 0 2 3 5 8 |
16 0 4 6 10 48 |
|
|
26 |
|
|
84 |
M.D. about median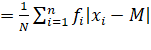 =
=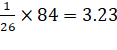
b.
Continuous
Frequency Distribution: It is a series in which the
data are classified into different class interval without gaps along with their
respective frequencies.
i.
Mean Deviation about Mean: This is same as the discrete frequency distribution except that here ![]() represents the middle point of
the class interval.
represents the middle point of
the class interval.
M.D.(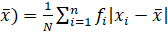
Question 5: Find the mean deviation about the mean for the data given
|
Income per day |
0-100 |
100-200 |
200-300 |
300-400 |
400-500 |
500-600 |
600-700 |
700-800 |
|
Number of persons |
4 |
8 |
9 |
10 |
7 |
5 |
4 |
3 |
Solution:
|
Income per day |
Mid-value |
|
|
|
|
|
0-100 100-200 200-300 300-400 400-500 500-600 600-700 700-800 |
50 150 250 350 450 550 650 750 |
4 8 9 10 7 5 4 3 |
200 1200 2250 3500 3150 2750 2600 2250 |
308 208 108 8 92 192 292 392 |
1232 1664 972 80 644 960 1168 1178 |
|
|
|
50 |
17900 |
|
7896 |
Mean ![]() =
= 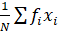 =
=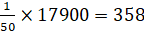
M.D. about mean 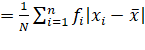 =
=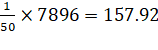
ii.
Mean Deviation about Median:
Here, Median =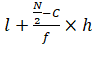
Where, l = lower limit,
N = sum of frequencies,
f= the frequency,
C = cumulative frequency,
h = width of the median class.
Then, M.D. (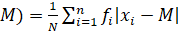
Question 6: Find the mean
deviation about median for the data given
|
Marks |
0-10 |
10-20 |
20-30 |
30-40 |
40-50 |
50-60 |
|
Number of Girls |
6 |
8 |
14 |
16 |
4 |
2 |
Solution:
|
Marks |
Mid value |
|
c.f. |
|
|
|
0-10 10-20 20-30 30-40 40-50 50-60 |
5 15 25 35 45 55 |
6 8 14 16 4 2 |
6 14 28 44 48 50 |
22.86 12.86 2.86 7.14 17.14 27.14 |
137.16 102.88 40.04 114.24 68.56 54.28 |
|
|
|
50 |
|
|
517.16 |
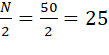
Median class is 20-30
Median= 20+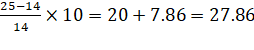
M.D. about median 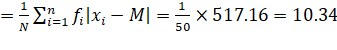
III.
Limitations of Mean Deviation:
i.
Not
easily understandable.
ii.
Its
calculation is not easy and time-consuming.
iii.
Dependent
on the change of scale.
iv.
Ignorance
of negative sign creates artificiality and becomes useless for further
mathematical treatment.
Variance:
Mean of the square of the squares of the deviations from mean is called
the variance.
Variance,
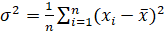
Standard Deviation:
A standard deviation is the positive square root of the
arithmetic mean of the squares of the deviations of the given values from their
arithmetic mean. It is denoted by a Greek letter sigma, σ. It is
also referred to as root mean square deviation. The standard deviation is given
as
Standard Deviation, 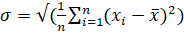
Question 7: Find the variance and
standard deviation deviation of the
following data
3,
4, 6, 5, 5, 3, 8, 1, 7, 5
Solution: Here x=3, 4, 6, 5, 5,
3, 8, 1, 7, 5.
![]()
n=10
Therefore,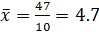
![]()
![]()
=259
S.D. = 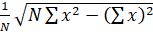 =
= 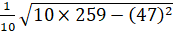 =
=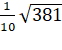 =
= 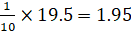
Variance =![]()
I.
Standard Deviation of a Discrete Frequency Distribution:
Let the given discrete frequency
distribution be
![]()
![]()
Standard
Deviation (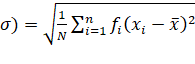
where, N= ![]()
Question 7: Find the variance and
standard deviation deviation of the
following data
|
|
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
|
|
4 |
4 |
5 |
15 |
8 |
5 |
4 |
5 |
Solution:
|
|
|
|
|
|
|
|
2 4 6 8 10 12 14 16 |
4 4 5 15 8 5 4 5 |
8 16 30 120 80 60 56 80 |
-7 -5 -3 -1 1 3 5 7 |
49 25 9 1 1 9 25 49 |
196 100 45 15 8 45 100 245 |
|
|
50 |
450 |
|
|
754 |
Mean, ![]()
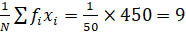
Variance, ![]()
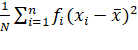 =
= 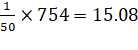
Standard Deviation, ![]()
II.
Standard Deviation of a Continuous Frequency
Distribution:
If there is a frequency distribution of n class defined by its
mid-point ![]() with frequency
with frequency ![]() , the standard deviation will be obtained by the formula
, the standard deviation will be obtained by the formula
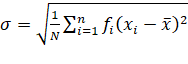
where,
N= ![]()
III.
Another Formula for Standard Deviation:
Standard
Deviation (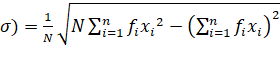
Question 8: Find the mean,variance
and standard deviation of the following frequency distribution
|
Class |
0-30 |
30-60 |
60-90 |
90-120 |
120-150 |
150-180 |
180-210 |
|
Frequencies |
2 |
3 |
5 |
10 |
3 |
5 |
2 |
Solution:
|
Classes |
Mid values |
|
|
|
|
|
0-30 30-60 60-90 90-120 120-150 150-180 180-210 |
15 45 75 105 135 165 195 |
2 3 5 10 3 5 2 |
-3 -2 -1 0 1 2 3 |
-6 -6 -5 0 3 10 6 |
18 12 5 0 3 20 18 |
|
|
|
30 |
|
2 |
76 |
Mean,![]() A+
A+ 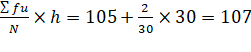
Variance, 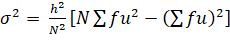 =
=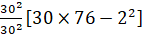
=![]()
Standard deviation, ![]()
Analysis of Frequency
Distributions:
The measure of variability which is independent of units is called
coefficient of variation.
Coefficient of Variation is defined as
C.V.=![]()
where ![]() and
and ![]() are the standard deviation and
mean of data.
are the standard deviation and
mean of data.
I.
Comparison of Two Frequency Distribution with Same Mean:
Let ![]() and
and ![]() be the mean and standard
deviation of the first distribution, and
be the mean and standard
deviation of the first distribution, and
![]() and
and ![]() be the mean and standard
deviation of the second distribution.
be the mean and standard
deviation of the second distribution.
C.V.(1st
distribution)=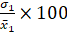
C.V.(2nd
distribution)=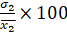
Given ![]() =
=![]() =
=![]()
Then,
C.V.(1st
distribution)=![]()
C.V.(2nd
distribution)=![]()
From above it is
clear that the two C.V.s can be compared on the basis of values of ![]() and
and ![]() only,
only,
Thus, we say that for
two series with equal means, the series with greater S.D. (or variance) is
called more variable or dispersed that the other. Also, the series with lesser
value of S.D. (or variance) is said to be more consistent than the other.
Question 9: From the prices of
shares X and Y below, find out which is more stable in value:
|
X |
35 |
54 |
52 |
53 |
56 |
58 |
52 |
50 |
51 |
49 |
|
Y |
108 |
107 |
105 |
105 |
106 |
107 |
104 |
103 |
104 |
101 |
Solution:
|
X |
Y |
|
|
|
|
|
35 54 52 53 56 58 52 50 51 49 |
108 107 105 105 106 107 104 103 104 101 |
-16 3 1 2 5 7 1 -1 0 -2 |
3 2 0 0 1 2 -1 -2 -1 -4 |
256 9 1 4 25 49 1 1 0 4 |
9 4 0 0 1 4 1 4 1 16 |
|
510 |
1050 |
|
|
350 |
40 |
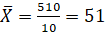
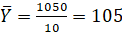
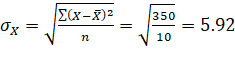
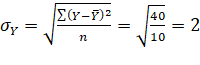
C.V. of X= 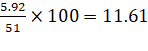
C.V. of Y = 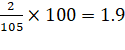
C.V. of Y![]() C.V. of X
C.V. of X
Thus, prices of share Y are more stable.