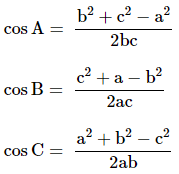Trigonometric
Functions
Measurement of Angle
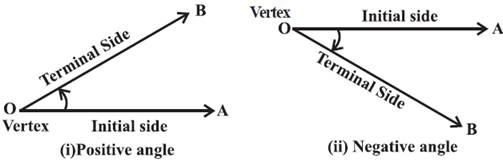
Angle
is a measure of rotation of a given ray about its initial point. The original
ray is called the initial side and the final position of the
ray after rotation is called the terminal side of the angle.
The point of rotation is called the vertex.
If
the direction of rotation is anticlockwise, the angle is said to be positive
and if the direction of rotation is clockwise, then the angle is negative
Degree:
If
a rotation from the initial side to terminal side is 13601360th of
a revolution, the angle is said to have a measure of one degree (1°).
One
degree is divided into 60 minutes, and a minute is divided into 60 seconds.
That is, one sixtieth of a degree is called a minute, written as
1′, and one sixtieth of a minute is called a second, written
as 1″.
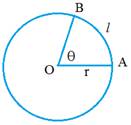
Radian:
Angle
subtended at the centre by an arc of length 1 unit in a unit circle (circle of
radius 1 unit) is said to have a measure of 1 radian.
One complete
revolution of the initial side subtends an angle of 2π radian.
In a circle of radius r, an arc of
length l will subtend an angle θ radian at the centre,
given by,

1°
= 60′ and 1′= 60′′
Some
Important Angle Measures in Degree and Radian

Relation
between radian and real numbers
Radian measures and real numbers can
be considered as one and the same. Consider the line PAQ which is tangent to
the circle at A. Let the point A represent the real number zero, AP represents
positive real numbers and AQ represents negative real numbers. If we rope the
line AP in the anticlockwise direction along the circle, and AQ in the
clockwise direction, then every real number will correspond to a radian measure
and conversely.
Trigonometric
Functions
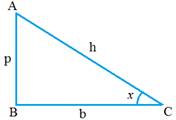
Trigonometric
ratios for an angle are the ratio of sides of a right angled triangle.
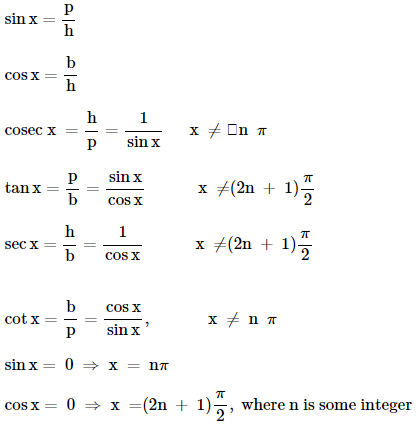
sin2 x + cos2 x = 1
1 +
tan2 x = sec2 x
1 +
cot2 x =
cosec2 x
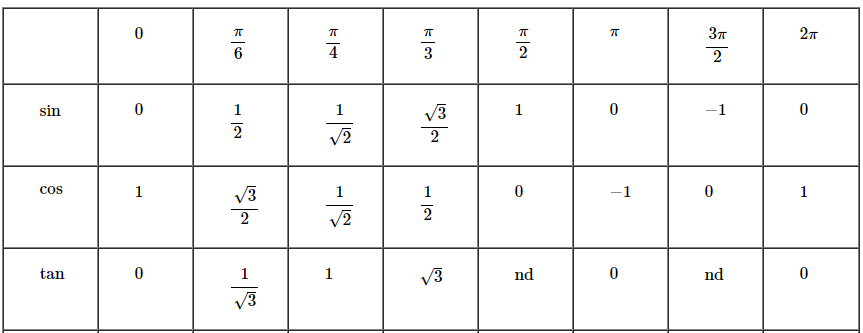
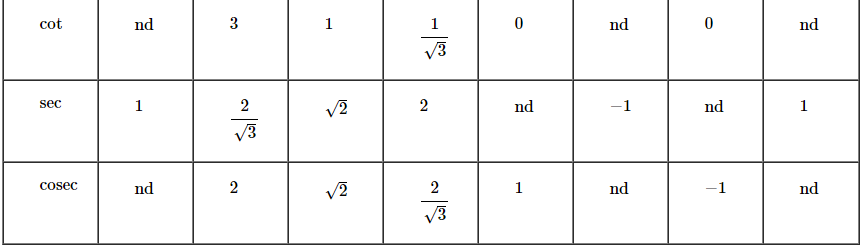
Values of trigonometric ratios of some common
angles
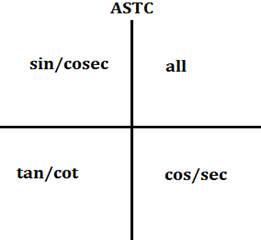
Signs of Trigonometric Functions
Trends
of Trigonometric Functions
|
f |
Q I |
Q II |
Q III |
Q IV |
|
|
sin |
increases
from 0 to 1 |
decreases
from 1 to 0 |
decreases
from 0 to -1 |
increases
from -1 to 0 |
|
|
cos |
decreases
from 1 to 0 |
decreases
from 0 to -1 |
increases
from -1 to 0 |
increases
from 0 to 1 |
|
|
tan |
increases
from 0 to
∞ |
increases
from -∞
to 0 |
increases
from 0 to
∞ |
increases
from -∞
to 0 |
|
|
cot |
decreases
from ∞ to
0 |
decreases
from 0 to
-∞ |
decreases
from ∞ to
0 |
decreases
from 0 to
-∞ |
|
|
sec |
increases
from 1 to
∞ |
increases
from -∞ to -1 |
decreases
from -1 to -∞ |
decreases
from ∞ to
1 |
|
|
cosec |
decreases
from ∞ to
1 |
increases
from 1 to
∞ |
increases
from -∞
to -1 |
decreases
from -1
to-∞ |
|
Graphical Representation of
Trigonometric Functions
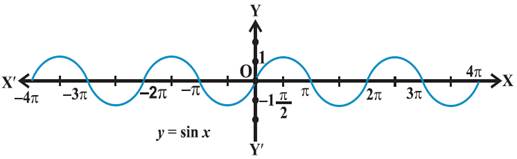
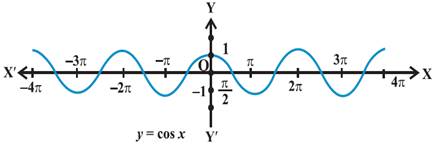
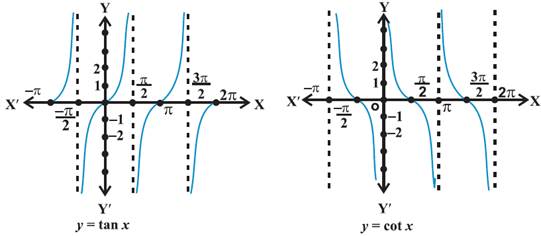
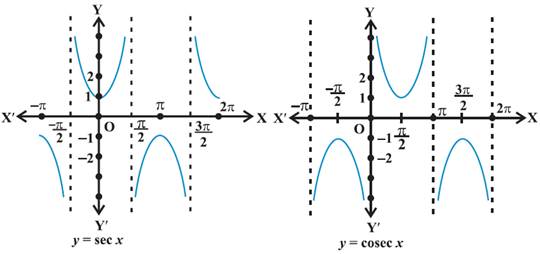
Important Trigonometric Formulae
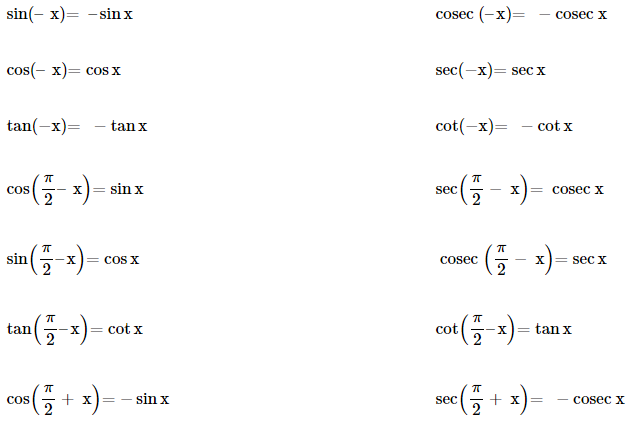
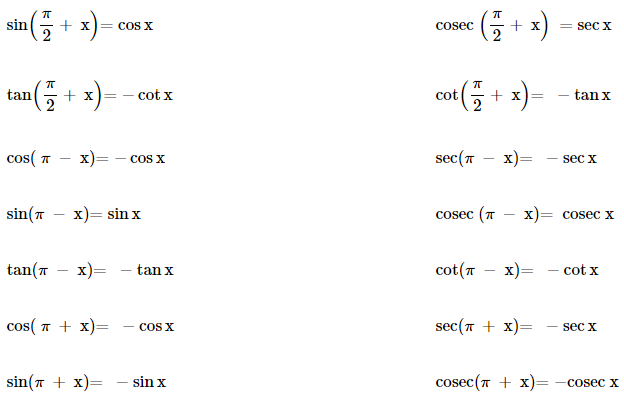
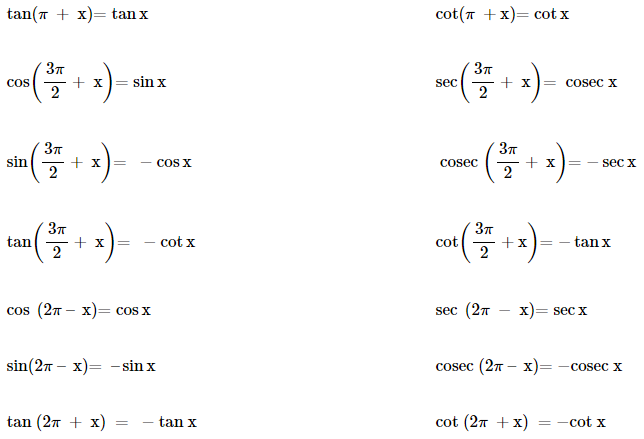
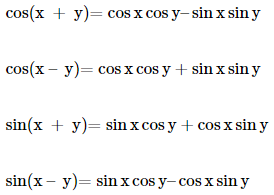
If none of the angles x, y and (x + y) is an odd multiple of
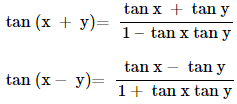
If none of the angles x, y and (x + y) is a multiple of π,
then
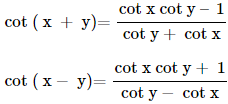
cos 2x = cos2x – sin2 x
= 2 cos2 x – 1
= 1 – 2 sin2 x
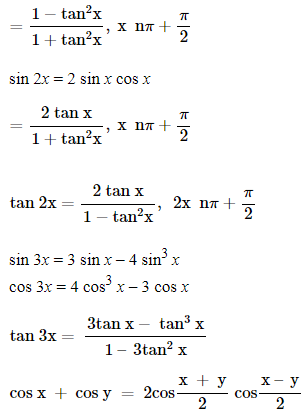
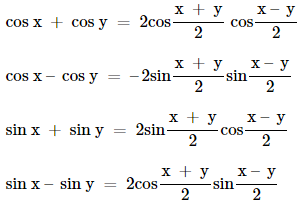
2 cos x cos y =
cos (x + y) + cos (x – y)
–2 sin x sin y =
cos (x + y) – cos (x – y)
2 sin x cos y =
sin (x + y) + sin (x – y)
2 cos x sin y =
sin (x + y) – sin (x – y)
Trigonometric Equations
- Equations involving trigonometric functions of a variable are
called trigonometric equations.
- The solutions of a trigonometric equation for which 0 ≤ x <
2π are called principal solutions.
- The expression involving integer ‘n’ which gives all
solutions of a trigonometric equation is called the general
solution.
Theorem 1 - For
any real numbers x and y,
sin x = sin y ⇒ x =
nπ + (–1)n y, where n ∈ Z
Theorem 2 - For
any real numbers x and y,
cos x = cos y,
⇒ x =
2nπ ± y, where n ∈ Z
Theorem 3 - If x and y are
not odd mulitple of π/2, then
tan x = tan y ⇒ x = nπ
+ y, where n ∈ Z
Formulae for angles of a triangle
Sine formula
In
any triangle, sides are proportional to the sines of the opposite angles. Let
A, B and C be angles of a triangle and a, b and c be lengths of sides opposite
to angles A, B and C respectively, then
![]()
Cosine formulae
Let A, B and C be angles of a triangle
and a, b and c be lengths of sides opposite to angles A, B and C respectively,
then
a2 = b2 + c2 – 2bc cos A
b2 = c2 + a2 – 2ca cos B
c2 = a2 + b2 – 2ab cos C
That is,