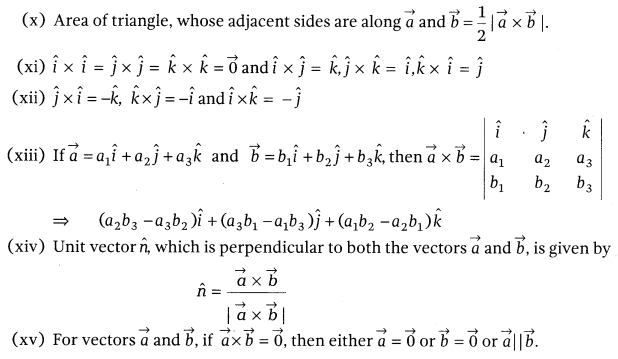Vector Algebra

Vector:

Those quantities which have magnitude, as well as direction, are called vector quantities or vectors.
Note: Those quantities which have only magnitude and no direction, are called scalar quantities.

Representation of Vector:

A directed line segment has magnitude as well as direction, so it is called vector denoted as $\vec { AB }$ or simply as $\vec { a }$ . Here, the point A from where the vector $\vec { AB }$ starts is called its initial point and the point B where it ends is called its terminal point.

Magnitude of a Vector:

The length of the vector $\vec { AB }$ or $\vec { a }$ is called magnitude of $\vec { AB }$ or $\vec { a }$ and it is represented by | $\vec { AB }$ | or | $\vec { a }$ | or a.
Note: Since, the length is never negative, so the notation | $\vec { a }$ |< 0 has no meaning.

Position Vector:

Let O(0, 0, 0) be the origin and P be a point in space having coordinates (x, y, z) with respect to the origin O. Then, the vector $\vec { OP }$ or $\vec { r }$ is called the position vector of the point P with respect to O. The magnitude of $\vec { OP }$ or $\vec { r }$ is given by

Direction Cosines:

If α, β and γ are the angles which a directed line segment OP makes with the positive directions of the coordinate axes OX, OY and OZ respectively, then cos α, cos β and cos γ are known as the direction cosines of OP and are generally denoted by the letters l, m and n respectively.

Vector Algebra Class 12 Notes Maths Chapter 10

i.e. l = cos α, m = cos β, n = cos γ Let l, m and n be the direction cosines of a line and a, b and c be three numbers, such that $\frac { l }{ a } =\frac { m }{ b } =\frac { n }{ c } =\vec { r }$ Note: l² + m² + n² = 1

Types of Vectors

Null vector or zero vector:

A vector, whose initial and terminal points coincide and magnitude is zero, is called a null vector and denoted as $\vec { 0 }$ . Note: Zero vector cannot be assigned a definite direction or it may be regarded as having any direction. The vectors $\vec { AA }$ , $\vec { BB }$ represent the zero vector.

Unit vector:

A vector of unit length is called unit vector. The unit vector in the direction of $\vec { a }$ is $\hat { a } =\frac { \vec { a } }{ \left| \vec { a } \right| }$

Collinear vectors:

Two or more vectors are said to be collinear, if they are parallel to the same line, irrespective of their magnitudes and directions, e.g. $\vec { a }$ and $\vec { b }$ are collinear, when $\vec { a } =\pm \lambda \vec { b }$ or $\vec { \left| a \right| } =\lambda \vec { \left| b \right| }$

Coinitial vectors:

Two or more vectors having the same initial point are called coinitial vectors.

Equal vectors:

Two vectors are said to be equal, if they have equal magnitudes and same direction regardless of the position of their initial points. Note: If $\vec { a }$ = $\vec { b }$ , then $\vec { \left| a \right| } =\vec { \left| b \right| }$ but converse may not be true.

Negative vector:

Vector having the same magnitude but opposite in direction of the given vector, is called the negative vector e.g. Vector $\vec { BA }$ is negative of the vector $\vec { AB }$ and written as $\vec { BA }$ = – $\vec { AB }$ .
Note: The vectors defined above are such that any of them may be subject to its parallel displacement without changing its magnitude and direction. Such vectors are called ‘free vectors’.

To Find a Vector when its Position Vectors of End Points are Given:

Let a and b be the position vectors of end points A and B respectively of a line segment AB. Then, $\vec { AB }$ = Position vector of $\vec { B }$ – Positron vector of $\vec { A }$
= $\vec { OB }$ – $\vec { OA }$ = $\vec { b }$ – $\vec { a }$

Addition of Vectors

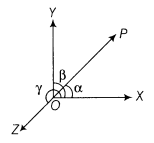
Triangle law of vector addition:

If two vectors are represented along two sides of a triangle taken in order, then their resultant is represented by the third side taken in opposite direction, i.e. in ∆ABC, by triangle law of vector addition, we have $\vec { BC }$ + $\vec { CA }$ = $\vec { BA }$ Note: The vector sum of three sides of a triangle taken in order is $\vec { 0 }$ .

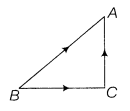
Vector Algebra Class 12 Notes Maths Chapter 10

Parallelogram law of vector addition:

If two vectors are represented along the two adjacent sides of a parallelogram, then their resultant is represented by the diagonal of the sides. If the sides OA and OC of parallelogram OABC represent $\vec { OA }$ and $\vec { OC }$ respectively, then we get
$\vec { OA }$ + $\vec { OC }$ = $\vec { OB }$

Vector Algebra Class 12 Notes Maths Chapter 10

Note: Both laws of vector addition are equivalent to each other.

Properties of vector addition

Commutative:

For vectors $\vec { a }$ and $\vec { b }$ , we have $\vec { a } +\vec { b } =\vec { b } +\vec { a }$

Associative:

For vectors $\vec { a }$ , $\vec { b }$ and $\vec { c }$ , we have $\vec { a } +\left( \vec { b } +\vec { c } \right) =\left( \vec { a } +\vec { b } \right) +\vec { c }$
Note: The associative property of vector addition enables us to write the sum of three vectors $\vec { a }$ , $\vec { b }$ and $\vec { c }$ as $\vec { a } +\vec { b } +\vec { c }$ without using brackets.

Additive identity:

For any vector $\vec { a }$ , a zero vector $\vec { 0 }$ is its additive identity as $\vec { a } +\vec { 0 } =\vec { a }$

Additive inverse:

For a vector $\vec { a }$ , a negative vector of $\vec { a }$ is its additive inverse as $\vec { a } +\left( \vec { -a } \right) =\vec { 0 }$

Multiplication of a Vector by a Scalar:

Let $\vec { a }$ be a given vector and λ be a scalar, then multiplication of vector $\vec { a }$ by scalar λ, denoted as λ $\vec { a }$ , is also a vector, collinear to the vector $\vec { a }$ whose magnitude is |λ| times that of vector $\vec { a }$ and direction is same as $\vec { a }$ , if λ > 0, opposite of $\vec { a }$ , if λ < 0 and zero vector, if λ = 0.
Note: For any scalar λ, λ . $\vec { 0 }$ = $\vec { 0 }$ .

Properties of Scalar Multiplication:

For vectors $\vec { a }$ , $\vec { b }$ and scalars p, q, we have
(i) p( $\vec { a }$ + $\vec { a }$ ) = p $\vec { a }$ + p $\vec { a }$
(ii) (p + q) $\vec { a }$ = p $\vec { a }$ + q $\vec { a }$
(iii) p(q $\vec { a }$ ) = (pq) $\vec { a }$
Note: To prove $\vec { a }$ is parallel to $\vec { b }$ , we need to show that $\vec { a }$ = λ $\vec { a }$ , where λ is a scalar.

Components of a Vector:

Let the position vector of P with reference to O is $\vec { OP } =\vec { r } =x\hat { i } +y\hat { j } +z\hat { k }$ , this form of any vector is-called its component form. Here, x, y and z are called the scalar components of $\vec { r }$ and $x\hat { i }$ , $y\hat { j }$ and $z\hat { k }$ are called the vector components of $\vec { r }$ along the respective axes.

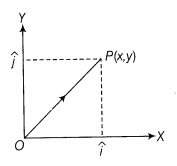
Two dimensions:

If a point P in a plane has coordinates (x, y), then $\vec { OP } =x\hat { i } +y\hat { j }$ , where $\hat { i }$ and $\hat { j }$ are unit vectors along OX and OY-axes, respectively.
Then, $\left| \vec { OP } \right| =\sqrt { { x }^{ 2 }+{ y }^{ 2 } }$

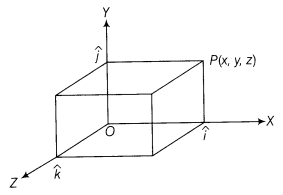
Vector Algebra Class 12 Notes Maths Chapter 10

Three dimensions:

If a point P in a plane has coordinates (x, y, z), then $\vec { OP } =x\hat { i } +y\hat { j } +z\hat { k }$ , where $\hat { i }$ , $\hat { j }$ and $\hat { k }$ are unit vectors along OX, OY and OZ-axes, respectively. Then, $\left| \vec { OP } \right| =\sqrt { { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 } }$

Vector Algebra Class 12 Notes Maths Chapter 10

Vector Joining of Two Points:

If P₁(x₁, y₁, z₁) and P₂(x₂, y₂, z₂) are any two points, then the vector joining P₁ and P₂ is the vector $\vec { { P }_{ 1 }{ P }_{ 2 } }$
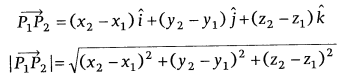
Vector Algebra Class 12 Notes Maths Chapter 10

Section Formula:

Position vector $\vec { OR }$ of point R, which divides the line segment joining the points A and B with position vectors $\vec { a }$ and $\vec { b }$ respectively, internally in the ratio m : n is given by
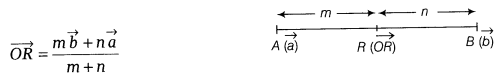
Vector Algebra Class 12 Notes Maths Chapter 10

For external division,
Vector Algebra Class 12 Notes Maths Chapter 10

Note: Position vector of mid-point of the line segment joining end points A( $\vec { a }$ ) and B( $\vec { b }$ ) is given by $\vec { OR } =\frac { \vec { a } +\vec { b } }{ 2 }$

Dot Product of Two Vectors:

If θ is the angle between two vectors $\vec { a }$ and $\vec { b }$ , then the scalar or dot product denoted by $\vec { a }$ . $\vec { b }$ is given by $\vec { a } \cdot \vec { b } =\left| \vec { a } \right| \left| \vec { b } \right| cos\theta$ , where 0 ≤ θ ≤ π.
Note:
(i) $\vec { a } \cdot \vec { b }$ is a real number
(ii) If either $\vec { a } =\vec { 0 }$ or $\vec { b } =\vec { 0 }$ , then θ is not defined.

Properties of dot product of two vectors $\vec { a }$ and $\vec { b }$ are as follows:
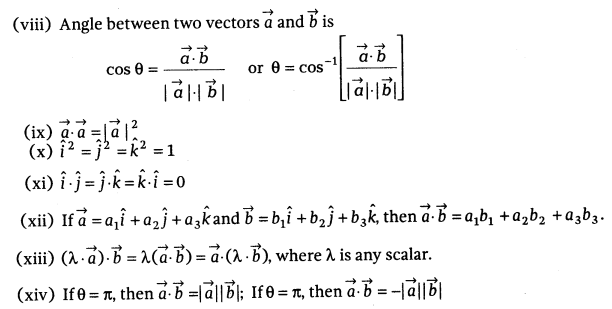
Vector Algebra Class 12 Notes Maths Chapter 10

Vector (or Cross) Product of Vectors:

If θ is the angle between two non-zero, non-parallel vectors $\vec { a }$ and $\vec { b }$ , then the cross product of vectors, denoted by $\vec { a } \times \vec { b }$ is given by

where, $\hat { n }$ is a unit vector perpendicular to both $\vec { a }$ and $\vec { b }$ , such that $\vec { a }$ , $\vec { b }$ and $\hat { n }$ form a right handed system.
Note
(i) $\vec { a } \times \vec { b }$ is a vector quantity, whose magnitude is $\left| \vec { a } \times \hat { b } \right| =\left| \vec { a } \right| \vec { \left| b \right| } sin\theta$
(ii) If either $\vec { a } =\vec { 0 }$ or $\vec { b } =\vec { 0 }$ , then0is not defined.

Properties of cross product of two vectors $\vec { a }$ and $\vec { b }$ are as follows:
Vector Algebra Class 12 Notes Maths Chapter 10