Three Dimensional Geometry

Direction Cosines of a Line:

If the directed line OP makes angles α, β, and γ with positive X-axis, Y-axis and Z-axis respectively, then cos α, cos β, and cos γ, are called direction cosines of a line. They are denoted by l, m, and n. Therefore, l = cos α, m = cos β and n = cos γ. Also, sum of squares of direction cosines of a line is always 1,
i.e. l² + m² + n² = 1 or cos² α + cos² β + cos² γ = 1
Note: Direction cosines of a directed line are unique.

Direction Ratios of a Line:

Number proportional to the direction cosines of a line, are called direction ratios of a line.
(i) If a, b and c are direction ratios of a line, then $\frac { l }{ a }$ = $\frac { m }{ b }$ = $\frac { n }{ c }$
(ii) If a, b and care direction ratios of a line, then its direction cosines are
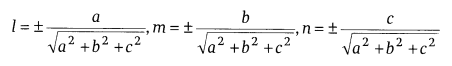
Three Dimensional Geometry Class 12 Notes Maths Chapter 11
(iii) Direction ratios of a line PQ passing through the points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) are x₂ – x₁, y₂ – y₁ and z₂ – z₁ and direction cosines are

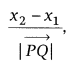
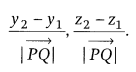
Note:
(i) Direction ratios of two parallel lines are proportional.
(ii) Direction ratios of a line are not unique.

Straight line:

A straight line is a curve, such that all the points on the line segment joining any two points of it lies on it.

Equation of a Line through a Given Point and parallel to a given vector $\vec { b }$
Vector form $\vec { r } =\vec { a } +\lambda \vec { b }$
where, $\vec { a }$ = Position vector of a point through which the line is passing
$\vec { b }$ = A vector parallel to a given line

Cartesian form
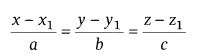
Three Dimensional Geometry Class 12 Notes Maths Chapter 11
where, (x₁, y₁, z₁) is the point through which the line is passing through and a, b, c are the direction ratios of the line.
If l, m, and n are the direction cosines of the line, then the equation of the line is

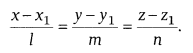
Remember point: Before we use the DR’s of a line, first we have to ensure that coefficients of x, y and z are unity with a positive sign.

Equation of Line Passing through Two Given Points
Vector form:

$\vec { r } =\vec { a } +\lambda \left( \vec { b } -\vec { a } \right)$ , λ ∈ R, where a and b are the position vectors of the points through which the line is passing.

Cartesian form
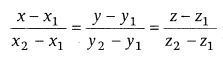
Three Dimensional Geometry Class 12 Notes Maths Chapter 11
where, (x₁, y₁, z₁) and (x₂, y₂, z₂) are the points through which the line is passing.

Angle between Two Lines
Vector form:

Angle between the lines $\vec { r } =\vec { { a }_{ 1 } } +\lambda \vec { { b }_{ 1 } }$ and $\vec { r } =\vec { { a }_{ 2 } } +\mu \vec { { b }_{ 2 } }$ is given as
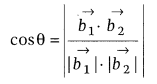
Three Dimensional Geometry Class 12 Notes Maths Chapter 11

Cartesian form:

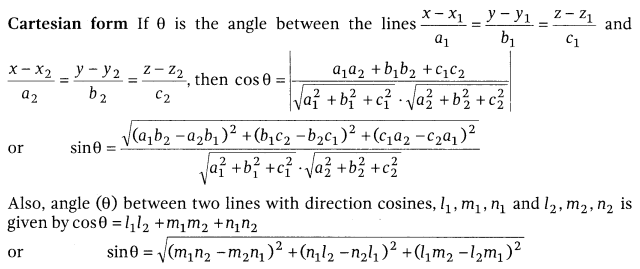
Three Dimensional Geometry Class 12 Notes Maths Chapter 11

Condition of Perpendicularity:

Two lines are said to be perpendicular, when in vector form $\vec { { b }_{ 1 } } \cdot \vec { { b }_{ 2 } } =0$ ; in cartesian form a₁a₂ + b₁b₂ + c₁c₂ = 0
or l₁l₂ + m₁m₂ + n₁n₂ = 0 [direction cosine form]

Condition that Two Lines are Parallel:

Two lines are parallel, when in vector form $\vec { { b }_{ 1 } } \cdot \vec { { b }_{ 2 } } =\left| \vec { { b }_{ 1 } } \right| \left| \vec { { b }_{ 2 } } \right|$ ; in cartesian form $\frac { { a }_{ 1 } }{ { a }_{ 2 } } =\frac { { b }_{ 1 } }{ { b }_{ 2 } } =\frac { { c }_{ 1 } }{ { c }_{ 2 } }$
or
$\frac { { l }_{ 1 } }{ { l }_{ 2 } } =\frac { { m }_{ 1 } }{ { m }_{ 2 } } =\frac { { n }_{ 1 } }{ { n }_{ 2 } }$
[direction cosine form]

Shortest Distance between Two Lines:

Two non-parallel and non-intersecting straight lines, are called skew lines.
For skew lines, the line of the shortest distance will be perpendicular to both the lines.
Vector form:

If the lines are $\vec { r } =\vec { { a }_{ 1 } } +\lambda \vec { { b }_{ 1 } }$ and $\vec { r } =\vec { { a }_{ 2 } } +\lambda \vec { { b }_{ 2 } }$ . Then, shortest distance
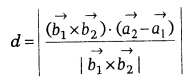
Three Dimensional Geometry Class 12 Notes Maths Chapter 11
where $\vec { { a }_{ 2 } }$ , $\vec { { a }_{ 1 } }$ are position vectors of point through which the line is passing and $\vec { { b }_{ 1 } }$ , $\vec { { b }_{ 2 } }$ are the vectors in the direction of a line.

Cartesian form:

If the lines are
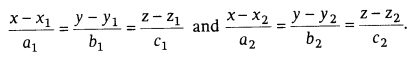
Three Dimensional Geometry Class 12 Notes Maths Chapter 11
Then, shortest distance,

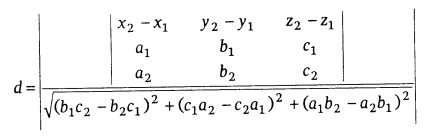
Distance between two Parallel Lines:

If two lines l₁ and l₂ are parallel, then they are coplanar. Let the lines be $\vec { r } =\vec { { a }_{ 1 } } +\lambda \vec { b }$ and $\vec { r } =\vec { { a }_{ 2 } } +\mu \vec { b }$ , then the distance between parallel lines is
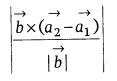
Three Dimensional Geometry Class 12 Notes Maths Chapter 11
Note: If two lines are parallel, then they both have same DR’s.

Distance between Two Points:

The distance between two points P (x₁, y₁, z₁) and Q (x₂, y₂, z₂) is given by
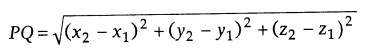
Three Dimensional Geometry Class 12 Notes Maths Chapter 11

Mid-point of a Line:

The mid-point of a line joining points A (x₁, y₁, z₁) and B (x₂, y₂, z₂) is given by
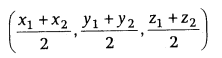
Three Dimensional Geometry Class 12 Notes Maths Chapter 11

Plane:

A plane is a surface such that a line segment joining any two points of it lies wholly on it. A straight line which is perpendicular to every line lying on a plane is called a normal to the plane.

Equations of a Plane in Normal form

Vector form:

The equation of plane in normal form is given by $\vec { r } \cdot \vec { n } =d$ , where $\vec { n }$ is a vector which is normal to the plane.

Cartesian form:

The equation of the plane is given by ax + by + cz = d, where a, b and c are the direction ratios of plane and d is the distance of the plane from origin.
Another equation of the plane is lx + my + nz = p, where l, m, and n are direction cosines of the perpendicular from origin and p is a distance of a plane from origin.
Note: If d is the distance from the origin and l, m and n are the direction cosines of the normal to the plane through the origin, then the foot of the perpendicular is (ld, md, nd).

Equation of a Plane Perpendicular to a given Vector and Passing Through a given Point

Vector form:

Let a plane passes through a point A with position vector $\vec { a }$ and perpendicular to the vector $\vec { n }$ , then $\left( \vec { r } -\vec { a } \right) \cdot \vec { n } =0$
This is the vector equation of the plane.

Cartesian form:

Equation of plane passing through point (x₁, y₁, z₁) is given by
a (x – x₁) + b (y – y₁) + c (z – z₁) = 0 where, a, b and c are the direction ratios of normal to the plane.

Equation of Plane Passing through Three Non-collinear Points

Vector form:

If $\vec { a }$ , $\vec { b }$ and $\vec { c }$ are the position vectors of three given points, then equation of a plane passing through three non-collinear points is .

Cartesian form:

If (x₁, y₁, z₁) (x₂, y₂, z₂) and (x₃, y₃, z₃) are three non-collinear points, then equation of the plane is
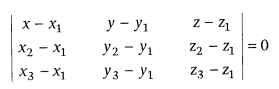
Three Dimensional Geometry Class 12 Notes Maths Chapter 11
If above points are collinear, then

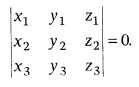
Equation of Plane in Intercept Form:

If a, b and c are x-intercept, y-intercept and z-intercept, respectively made by the plane on the coordinate axes, then equation of plane is $\frac { x }{ a } +\frac { y }{ b } +\frac { z }{ c } =1$

Equation of Plane Passing through the Line of Intersection of two given Planes

Vector form:

If equation of the planes are $\vec { r } \cdot \vec { { n }_{ 1 } } ={ d }_{ 1 }$ and $\vec { r } \cdot \vec { { n }_{ 2 } } ={ d }_{ 2 }$ , then equation of any plane passing through the intersection of planes is
$\vec { r } \cdot \left( \vec { { n }_{ 1 } } +\lambda \vec { { n }_{ 2 } } \right) ={ d }_{ 1 }+\lambda { d }_{ 2 }$
where, λ is a constant and calculated from given condition.

Cartesian form:

If the equation of planes are a₁x + b₁y + c₁z = d₁ and a₂x + b₂y + c₂z = d₂, then equation of any plane passing through the intersection of planes is a₁x + b₁y + c₁z – d₁ + λ (a₂x + b₂y + c₂z – d₂) = 0
where, λ is a constant and calculated from given condition.

Coplanarity of Two Lines

Vector form:

If two lines $\vec { r } =\vec { { a }_{ 1 } } +\lambda \vec { { b }_{ 1 } }$ and $\vec { r } =\vec { { a }_{ 2 } } +\mu \vec { { b }_{ 2 } }$ are coplanar, then

Cartesian form:

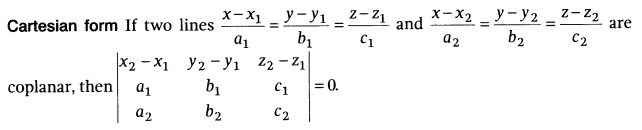
Three Dimensional Geometry Class 12 Notes Maths Chapter 11

Angle between Two Planes: Let θ be the angle between two planes.

Vector form:

If $\vec { { n }_{ 1 } }$ and $\vec { { n }_{ 2 } }$ are normal to the planes and θ be the angle between the planes $\vec { r } \cdot \vec { { n }_{ 1 } } ={ d }_{ 1 }$ and $\vec { r } \cdot \vec { { n }_{ 2 } } ={ d }_{ 2 }$ , then θ is the angle between the normal to the planes drawn from some common points.
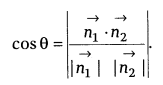
Three Dimensional Geometry Class 12 Notes Maths Chapter 11
Note: The planes are perpendicular to each other, if $\vec { { n }_{ 1 } } \cdot \vec { { n }_{ 2 } } =0$ and parallel, if $\vec { { n }_{ 1 } } \cdot \vec { { n }_{ 2 } } =\left| \vec { { n }_{ 1 } } \right| \left| \vec { { n }_{ 2 } } \right|$

Cartesian form:

If the two planes are a₁x + b₁y + c₁z = d₁ and a₂x + b₂y + c₂z = d₂, then
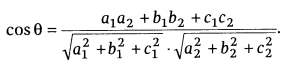
Three Dimensional Geometry Class 12 Notes Maths Chapter 11
Note: Planes are perpendicular to each other, if a₁a₂ + b₁b₂ + c₁c₂ = 0 and planes are parallel, if $\frac { { a }_{ 1 } }{ { a }_{ 2 } } =\frac { { b }_{ 1 } }{ { b }_{ 2 } } =\frac { { c }_{ 1 } }{ { c }_{ 2 } }$

Distance of a Point from a Plane

Vector form:

The distance of a point whose position vector is $\vec { a }$ from the plane
$\vec { r } \cdot \hat { n } =d\quad is\quad \left| d-\vec { a } \hat { n } \right|$

Note:
(i) If the equation of the plane is in the form $\vec { r } \cdot \vec { n } =d$ , where $\vec { n }$ is normal to the plane, then the perpendicular distance is $\frac { \left| \vec { a } \cdot \vec { n } -d \right| }{ \left| \vec { n } \right| }$
(ii) The length of the perpendicular from origin O to the plane $\vec { r } \cdot \vec { n } =d\quad is\quad \frac { \left| d \right| }{ \left| \vec { n } \right| }$ [∵ $\vec { a }$ = 0]

Cartesian form:

The distance of the point (x₁, y₁, z₁) from the plane Ax + By + Cz = D is
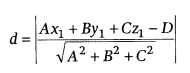
Three Dimensional Geometry Class 12 Notes Maths Chapter 11

Angle between a Line and a Plane

Vector form:

If the equation of line is $\vec { r } =\vec { a } +\lambda \vec { b }$ and the equation of plane is $\vec { r } \cdot \vec { n } =d$ , then the angle θ between the line and the normal to the plane is
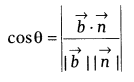
Three Dimensional Geometry Class 12 Notes Maths Chapter 11
and so the angle Φ between the line and the plane is given by 90° – θ,
i.e. sin(90° – θ) = cos θ

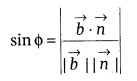
Cartesian form:

If a, b and c are the DR’s of line and lx + my + nz + d = 0 be the equation of plane, then
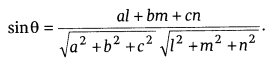
Three Dimensional Geometry Class 12 Notes Maths Chapter 11
If a line is parallel to the plane, then al + bm + cn = 0 and if line is perpendicular to the plane, then $\frac { a }{ l } =\frac { b }{ m } =\frac { c }{ n }$

Remember Points

(i) If a line is parallel to the plane, then normal to the plane is perpendicular to the line. i.e. a₁a₂ + b₁b₂ + c₁c₂ = 0
(ii) If a line is perpendicular to the plane, then DR’s of line are proportional to the normal of the plane.
i.e. $\frac { { a }_{ 1 } }{ { a }_{ 2 } } =\frac { { b }_{ 1 } }{ { b }_{ 2 } } =\frac { { c }_{ 1 } }{ { c }_{ 2 } }$
where, a₁, b₁ and c₁ are the DR’s of a line and a₂, b₂ and c₂ are the DR’s of normal to the plane.