An automobile manufacturer makes automobiles and trucks in a factory that is divided into two shops. Shop A, which performs the basic assembly operation, must work 5 man - days on each truck but only 2 man - days on each automobile. Shop B which performs finishing operations, must work 3 man - days for each automobile or truck that it produces. Because of men and machine limitations, shop A has 180 man - days per week available while shop B has 135 man - days per week. If the manufacturer makes a profit of Rs 30000 on each truck and Rs 2000 on each automobile, how many of each should he produce to maximize his profit? Formulate this as a LPP.
Matching exercise
Match the items on the right to the items on the left.
Step - 1
Step - 2
Step - 3
Let number of automobiles produces be x and let the number of trucks
Produced be y.
Let Z be the profit function to be maximized.
Z = 2000x + 30000y
The constraints are on the man hours worked
Shop A 2x + 5y ≤ 180 (i) assembly
Shop B 3x + 3y ≤ 135 (ii) finishing
x, y ≥ 0
Corner points can ve obtained from
2x = 3y + 5y = 180 ⇒ x = 0; y = 36 and x = 90; y = 0
3x + 3y ≤ 135 ⇒ x = 0; y = 45 and x = 45; y = 0
Solving (i) and (ii) gives x = 15 and y = 30
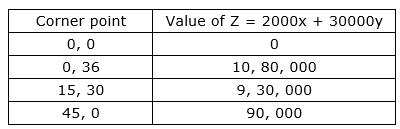
Thus 0 automobiles and 36 trucks give max. profit of Rs 10, 80, 000/ -