Two tailors A and B earn Rs 150 and Rs 200 per day respectively. A can stitch 6 shirts and 4 pants per day while B can stitch 10 shirts and 4 pants per day. Form a linear programming problem to minimize the labour cost to produce at least 60 shirts and 32 pants.
Matching exercise
Match the items on the right to the items on the left.
Step - 1
Step - 2
Step - 3
Step - 4
Step - 5
The data can be represented in a table below
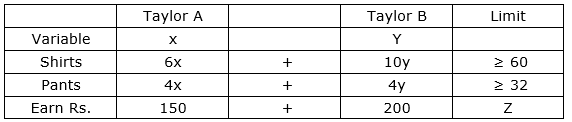
To minimize labour cost means to assume to minimize the earnings i.e,
Min Z = 150x + 200y
With constraints
x, y ≥ 0 at least 1 shirt and 1 pant is required
6x + 10y ≥ 60 require at least 60 shirts
4x + 4y ≥ 32 require at least 32 pants
On solving the above inequalities as equations, we get,
x = 5 and y = 3
other corner points obtained are [0, 6], [10, 0], [0, 8] and [8, 0]
The feasible region is the upper unbounded region A - E - D
Point E(5, 3) may not be minimal value. So, plot 150x + 200y < 1350 to see
If there is a common region with A - E - D.
The green line has no common point, therefore
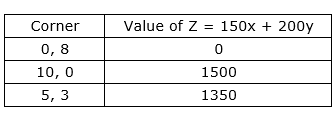
Thus, stitching 5 shirts and 3 pants minimizes labour cost to Rs 1350/ -