A farmer has a 100 - acre farm. He can sell the tomatoes, lettuce, or radishes he can raise. The price he can obtain is Rs 1 per kilogram for tomatoes, Rs 0.75 a head for lettuce and Rs 2 per kilogram for radishes. The average yield per acre is 2000 kgs for radishes, 3000 heads of lettuce and 1000 kilograms of radishes. Fertilizer is available at Rs 0.50 per kg and the amount required per acre is 100 kgs each for tomatoes and lettuce and 50 kilograms for radishes. Labour required for sowing, cultivating and harvesting per acre is 5 man - days for tomatoes and radishes and 6 man – days for lettuce. A total of 400 man - days of labour are available at ₹ 20 per man - day. Formulate this problem as a LPP to maximize the farmer’s total profit.

Matching exercise

Given information can be tabulated below

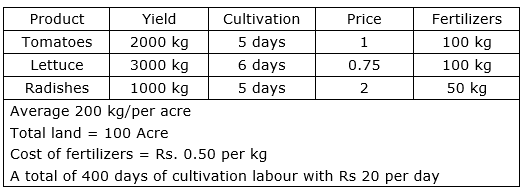
Let required quantity of field for tomatoes, lettuce and radishes be x, y and z
acre respectively.
Given, costs of cultivation and harvesting of tomatoes, lettuce and radishes are 5 x20 = Rs 100, 6 x20 = Rs 120, 5 x20 = Rs 100 respectively per acre. Cost of fertilizers for tomatoes, lettuce and radishes 100 x 0.50 = Rs 50, 100 x 0.50 = Rs 50 and 50 x0.50 = Rs 25 respectively per acre.
So, total costs of production of tomatoes, lettuce and radishes are (Rs 100 + 50)x = Rs 150x, (Rs 120 + 50)y = Rs 170y and radishes are (Rs 100 + 25)z = Rs 125z respectively total selling price of tomatoes, lettuce and radishes, according to yield are (Rs2000x1)x = Rs 2000x, (Rs3000 x0.75)y = Rs 2250y and (Rs1000x2)z = Rs 2000z respectively.
Let U be the total profit,
So,
U = (2000x - 150x) + (2250y - 170y) + (2000z - 125z)
U = 1850x + 2080y + 1875z
Given, farmer has 100 - acre farm
So, x + y + z ≤ 100 (First constraint)

Number of cultivation and harvesting days are 400 So, 5x + 6y + 5z ≤ 400
Hence, mathematical formulation of LPP is,
Find x, y, z which maximize U = 1850x + 2080y + 1875z
Subject to constraint,
x + y + z ≤ 100
5x + 6y + 5z ≤ 400
x, y, z ≥ 0 [Since farm used for cultivation cannot be less than zero.]