A firm has to transport at least 1200 packages daily using large vans which carry 200 packages each and small vans which can take 80 packages each. The cost of engaging each large van is Rs 400 and each small van is Rs 200. Not more than Rs 3000 is to be spent daily on the job and the number of large vans cannot exceed the number of small vans. Formulate this problem as a LPP given that the objective is to minimize cost.

Matching exercise

Given information can be tabulated as below:

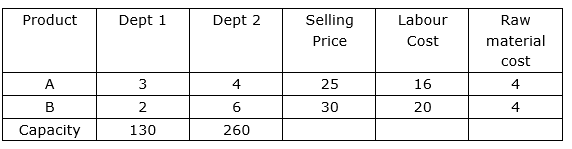
Let the required product of product A and B be x and y units respectively.
Given, labour cost and raw material cost of one unit of product A is Rs 16 and Rs 4, so total cost of product A is Rs 16 + Rs 4 = Rs 20
And given selling price of 1 unit of product A is Rs 25,
So, profit on one unit of product
A = 25 - 20 = Rs 5
Again, given labour cost and raw material cost of one unit of product B is Rs 20 and Rs 4 So, that cost of product B is Rs 20 + Rs 4 = Rs 24
And given selling price of 1 unit of product B is Rs 30

So, profit on one unit of product B = 30 - 24 = Rs 6
Hence, profits on x unit of product A and y units of product B are Rs 5x and Rs 6y respectively.
Let Z be the total profit, so,
Z = 5x + 6y
Given, production of one unit of product A and B need to process for 3 and 4 hours respectively in department 1, so production of x units of product A and y units of product B need to process for 3x and 4y hours respectively in Department 1. But total capacity of Department 1 is 130 hours,
So, 3x + 2y ≤ 130 (First constraint)

Given, production of one unit of product. A and B need to process for 4 and 6 hours respectively in department 2, so production of x units of product A and y units of product B need to process for 4x and 6y hours respectively in Department 2 but total capacity of Department 2 is 260 hours
So, 4x + 6y ≤ 260 (Second constraint)
Hence, mathematical formulation of LPP is,
Find x and y which
Maximize Z = 5x + 6y
Subject to constraint,
3x + 2y ≤ 130,
4x + 6y ≤ 260
x, y ≥ 0 [Since production cannot be less than zero]