A firm manufactures two products, each of which must be processed through two departments, 1 and 2. The hourly requirements per unit for each product in each department, the weekly capacities in each department, selling price per unit, labour cost per unit, and raw material cost per unit are summarized as follows : 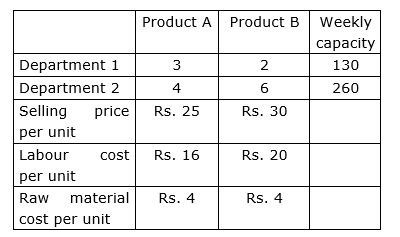 The problem is to determine the number of units to produce each product so as to maximize total contribution to profit. Formulate this as a LPP.
The problem is to determine the number of units to produce each product so as to maximize total contribution to profit. Formulate this as a LPP.
Matching exercise
Match the items on the right to the items on the left.
Step - 1
Step - 2
Step - 3
We have to maximize the profit by calculating the number of units needed to produce each product.
For Product A,
Cost Price per unit = Labour Cost + Raw material cost per unit
Cost Price per unit = 16 + 4 = Rs. 20
Selling Price per unit = Rs. 25
Profit per unit = S.P – C.P = 25 – 20 = Rs. 5
For Product B,
Cost Price per unit = Labour Cost + Raw material cost per unit
Cost Price per unit = 20 + 4 = Rs. 24
Selling Price per unit = Rs. 30
Profit per unit = S.P – C.P = 30 – 24 = Rs. 6
Let number of units produced of Product A be x and number of units produced of Product B be y.
Hence, Total Profit = 5 x + 6 y
To Maximize : z = 5 x + 6 y
For Department 1,
3 x + 2 y ≤ 130
For Department 2,
4 x + 6 y ≤ 260
Hence,
Z = 5 x + 6 y
3 x + 2 y ≤ 130
4 x + 6 y ≤ 260
x, y ≥ 0 [Since production cannot be less than zero]