A firm manufactures 3 products A, B and C. The profits are Rs. 3, Rs. 2 and Rs. 4 respectively. The firm has 2 machines and below is the required processing time in minutes for each machine on each product. 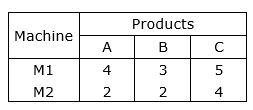Machines M1 and M2 have 2000 machine minutes respectively. The firm must manufacture 100 A’s, 200 B’s and 50 C’s but not more than 150 A’s. Set up a LPP to maximize the profit.

Matching exercise

Let, required production of product A, B and C be x, y and z units respectively.
Given, profit on one unit of product A, B and C are Rs 3, and Rs 2, Rs 4.
So, profit on x, y, z units of A, B, C Rs 3x, Rs 2y, Rs 4z.
Let U be the total profit, so
U = 3x + 2y + 4z
Given, one unit of product A, B and C requires 4, 3 and 5 minutes on machine M1. So, x units of A, y units of B and z units of C need 4x, 3y and 5z minutes. Maximum capacity on machine M1 is 2000 minutes, so,
4x + 3y + 5z ≤ 200 0 (First constraint)
Given, one unit of product A, B and C requires 2, 2 and 4 minutes on machine M2. So, x units of A, y units of B and z units of C require 2x, 2y and 4z minutes. Maximum capacity on machine M2 is 2500 minutes, so,
2x + 2y + 4z ≤ 250 0 (Second constraint)

Also, given that firm must manufacture more than 100 A’s, 200 B’s, 50 C’s also not more than 150 A’s, so,
100 ≤ x ≤ 150,
y ≥ 200 (Other constraints)
z ≥ 50
Hence, mathematical formulation of LPP is:
Find x, y and z which maximize U = 3x + 2y + 4z
Subject of constraints,
4x + 3y + 5z ≤ 2000
2x + 2y + 4z ≤ 2500
100 ≤ x ≤ 150,
y ≥ 200
z ≥ 50
and also, as production cannot be less than zero, so x, y ≥ 0