A rubber company is engaged in producing three types of tyres A, B and C. Each type requires processing in two plants, Plant I and Plant II. The capacities of the two plants, in the number of tyres per day, are as follows: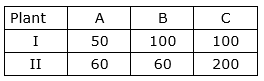 
The monthly demand for tyre A, B and C is 2500, 3000 and 7000 respectively. If plant I costs Rs 2500 per day, and plant II costs Rs 3500 per day to operate, how many days should each be run per month to minimize cost while meeting the demand? Formulate the problem as LPP.
Matching exercise
Match the items on the right to the items on the left.
Step - 1
Step - 2
Step - 3
lant I and II costs Rs 2500 per day and Rs 3500 per day respectively, so cost to run plant I and II are Rs 2500x and Rs 3500y per month.
Let Z be the total cost per month,
So, Z = 2500x + 3500y
Given, production of tyre A from plant I and II is 50 and 60 respectively, so production of tyre A from plant I and II will be 50x and 60y respectively per month but the maximum demand of tyre A is 2500 per month so,
100x + 60y ≥ 2500 [First constraint]
Given, production of tyre B from plant I and II is 100 and 60 respectively, so production of tyre B from plant I and II will be 100x and 60y per month respectively but the maximum demand of tyre B is 3000 per month, so
100x + 200y ≥ 3000 [Second constraint]
Given, production of tyre C from plant I and II is 100 and 200 respectively. So, production of tyre C from plant I and II will be 100x and 200y per month respectively but the maximum demand of tyre C is 7000 per day, so
100x + 200y ≥ 7000 [Third constraint]
Hence, mathematical formulation of LPP is,
Find x and y which
Minimize Z = 2500x + 3500y
Subject to constraint,
50x + 60y ≥ 2500
100x + 60y ≥ 3000
100x + 200y ≥ 7000
And, x, y ≥ 0 [Since number of days cannot be less than zero]
