To maintain his health a person must fulfil certain minimum daily requirements for several kinds of nutrients. Assuming that there are only three kinds of nutrients – calcium, protein and calories and the person’s diet consists of only two food items, I and II, whose price and nutrient contents are shown in the table below: 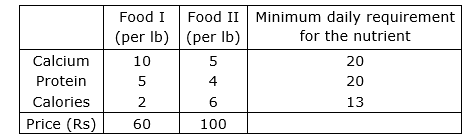 What combination of two food items will satisfy the daily requirement and entail the least cost? Formulate this as a LPP.
What combination of two food items will satisfy the daily requirement and entail the least cost? Formulate this as a LPP.
Matching exercise
Match the items on the right to the items on the left.
Step - 1
Step - 2
Step - 3
Step - 4
Step - 5
Let x and y be the packets of 25 gm of Food I and Food II purchased. Let Z be the price paid. Obviously, price has to be minimized.
Take a mass balance on the nutrients from Food I and II,
Calcium 10x + 4y ≥ 20
5x + 2y ≥ 10 (i)
Protein 5x + 5 y ≥ 20
x + y ≥ 4 (ii)
Calories 2x + 6y > 13 (iii)
These become the constraints for the cost function, Z to be minimized i.e., 0.6x + y = 7, given cost of Food I is Rs 0.6/ - and Rs 1/ - per lb
From (i), (ii) & (iii) we get points on the X & Y - axis as [0, 5] & [2, 0] ; [0, 4] & [ 4, 0] ; [0, 13/6] & [6.5, 0] Plotting these
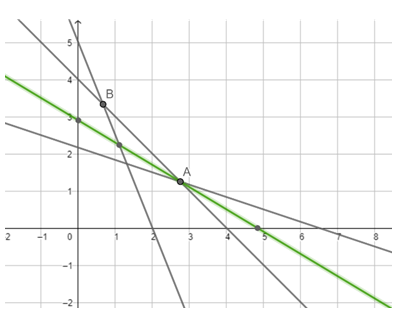
The smallest value of Z is 2.9 at the point (2.75, 1.25). We cannot say that the minimum value of z is 2.9 as the feasible region is unbounded.
Therefore, we have to draw the graph of the inequality 0.6x + y <2.9
Plotting this to see if the resulting line (in green) has any point common with the feasible region. Since there are no common points this is the minimum value of the function Z and the mix is
Food I = 2.75 lb; Food II = 1.25 lb; Price = Rs 2.9
When Z has an optimal value (maximum or minimum), where the variables x and y are subject to constraints described by linear inequalities., this optimal value must occur at a corner point (vertex) of the feasible region.
Here the feasible region is the unbounded region A - B - C - D
Computing the value of 7 at the corner points of the feasible region ABHG