A manufacturer can produce two products, A and B, during a given time period. Each of these products requires four different manufacturing operations: grinding, turning, assembling and testing. The manufacturing requirements in hours per unit of products A and B are given below. 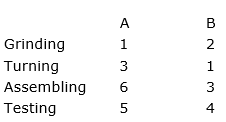The available capacities of these operations in hours for the given time period are: grinding 30; turning 60, assembling 200; testing 200. The contribution to profit is Rs 20 for each unit of A and Rs 30 for each unit of B. The firm can sell all that it produces at the prevailing market price. Determine the optimum amount of A and B to produce during the given time period. Formulate this as a LPP.

Matching exercise

Let required production of product A and B be x and y respectively
Given, profits on one unit of product A and B are Rs 2 and Rs 3 respectively, so profits on x units of product A and y units of product B are given by 2x and 3y respectively. Let Z be total profit, so
Z = 2x + 3y
Given, production of 1 unit of product A and B require 1 hour and 2 hours of grinding respectively, so, production of x units of product A and y units of product B require x hours and 2y hours of grinding respectively but the maximum time available for grinding is 3 hours, so
x + 2y ≤ 30 (First constraint)
Given, production of 1 unit of product A and B require 3 hours and 1 hours of turning respectively, so x units of product A and y units of product B require 3x hours and y hours of turning respectively but total time available for turning is 60 hours, so
3x + y ≤ 60 (Second constraint)

Given, production of 1 unit of product A and B require 6 hour and 3 hours of assembling respectively, so production of x units of product A and y units of product B require 6x hours and 3y hours of assembling respectively but total time available for assembling is 200 hours, so
6x + 3y ≤ 200 (Third constraint)
Given, production of 1 unit of product A and B require 5 hours and 4 hours of testing respectively, so production of x units of product A and y units of product B require 5x hours and 4y hours of testing respectively but total time available for testing is 200 hours, so
5x + 4y ≤ 200 (Fourth constraint)

Hence, mathematical formulation of LPP is,
Find x and y which
maximize Z = 2x + 3y
Subject to constraints,
x + 2y ≤ 30
3x + y ≤ 60
6x + 3y ≤ 200
5x + 4y ≤ 200
and, x, y ≥ 0 [Since production cannot be negative]