Vitamins A and B are found in two different foods F1 and F2. One unit of food F1 contains 2 units of vitamin A and 3 units of vitamin B. One unit of food F2 contains 4 units of vitamin A and 2 units of vitamin B. One unit of food F1 and F2 cost ₹ 50 and 25 respectively. The minimum daily requirements for a person of vitamin A and B is 40 and 50 units respectively. Assuming that anything in excess of daily minimum requirement of vitamin A and B is not harmful, find out the optimum mixture of food F1 and F2 at the minimum cost which meets the daily minimum requirement of vitamin A and B. Formulate this as a LPP.
Matching exercise
Match the items on the right to the items on the left.
Step - 1
Step - 2
Step - 3
Given information can be tabulated as below:
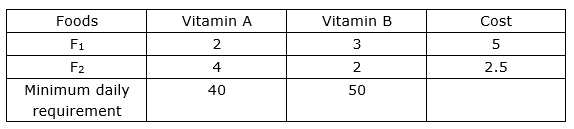
Let required quantity of food F1 be x units and quantity of food F2 be y units.
Given, costs of one unit of food F1 and F2 are Rs 5 and Rs 2.5 respectively, so costs of x units of food F1 and y units of food F2 are Rs 5x and Rs 2.5y respectively.
Let Z be the total cost, so
Z = 5x + 2.5y
Given, one unit of food F1 and food F2 contain 2 and 4 units of vitamin A respectively, so x unit of Food F1 and y units of food F2 contain 2x and 4y units of vitamin A respectively, but minimum requirement of vitamin A is 40 unit, so
2x + 4y ≥ 40 (First constraint)
Given, one unit of food F1 and food F2 contain 3 and 2 units of vitamin B respectively, so x unit of Food F1 and y units of food F2 contain 3x and 2y units of vitamin B respectively, but minimum daily requirement of vitamin B is 40 unit, so
3x + 2y ≥ 50 (Second constraint)
Hence, mathematical formulation of LPP is,
Find x and y which
Minimize Z = 5x + 2.5y
Subject to constraint,
2x + 4y ≥ 40
3x + 2y ≥ 50
x, y ≥ 0 [Since requirement of food F1 and F2 cannot be less zero.]