Step - 1

Step - 2

Step - 3

Step - 4

Step - 5

Step - 6

Step - 7

Given,
Objective function is: Z = 18x + 10y
Constraints are:
4x + y ≥ 20
2x + 3y ≥ 30
x, y ≥ 0
First convert the given inequations into corresponding equations and plot them:
4x + y ≥ 20 → 4x + y = 20 (corresponding equation)
Two coordinates required to plot the equation are obtained as:
Put, x = 0 ⇒ y = 20 (0,20) - - - - first coordinate.
Put, y = 0 ⇒ x = 5 (5,0) - - - - second coordinate
Join them to get the line.

As we know, Linear inequation will be a region in the plane, and we observe that the equation divides the XY plane into 2 halves only, so we need to check which region represents the given inequation,
If the given line does not pass through origin the just put (0,0) to check whether inequation is satisfied or not. If it satisfies the inequation origin side is the required region else the other side is the solution.
Similarly, we repeat the steps for other inequation also and find the common region.
2x + 3y ≥ 30 → 2x + 3y = 30 (corresponding equation)
Two coordinates required to plot the equation are obtained as:
Put, x = 0 ⇒ y = 10 (0,10) - - - - first coordinate.
Put, y = 0 ⇒ x = 15 (15,0) - - - - second coordinate
x = 0 is the y - axis and y = 0 is the x – axis

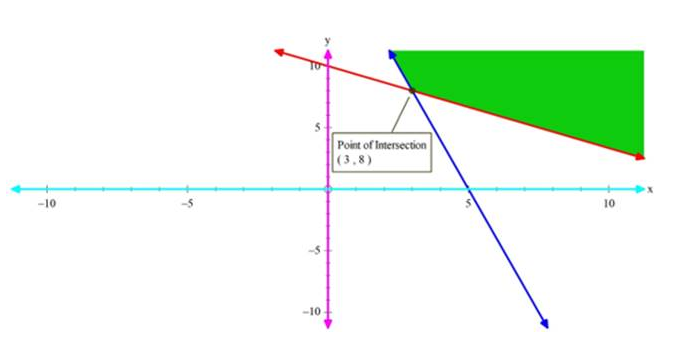
Hence we obtain a plot as shown in figure:
The shaded region in the above figure represents the region of a feasible solution.
Now to maximize our objective function, we need to find the coordinates of the corner points of the shaded region.
We can determine the coordinates graphically our by solving equations. But choose only those equations to solve which gives one of the corner coordinates of the feasible region.
Solving 2x + 3y = 30 and 4x + y = 20 gives (3, 8)
Similarly solving 4x + y = 20 and x = 0 gives (0, 20)
And solving 2x + 3y = 30 and y = 0 gives (15,0)

Now we have coordinates of the corner points so we will put them one by one to our objective function and will find at which point it is maximum.
∵ Z = 18x + 10y
∴ Z at (3, 8) = 18 × 3 + 8 × 10 = 134
Z at (0,20) = 18 × 0 + 10 × 20 = 200
Z at (15,0) = 18 × (15) + 10 × 0 = 270
Note: It is unbounded so we can’t say directly by seeing that z = 134 is minimum because there might be possibility that some other points from feasible region may result a smaller number.
In such a case minima will not be possible.
So we check this by setting inequation corresponding to the minimum value of Z.

∴ inequation is 18x + 10y < 134
As (0,0) satisfies the inequation, so it will bound its region towards origin and hence will not overlap with the feasible region.
∴ We can say that minima are possible.
We can see that Z is minimum at (3, 8) and min. value is 134
∴ Z is minimum at x = 3 and y = 8 ; and min value is 134.