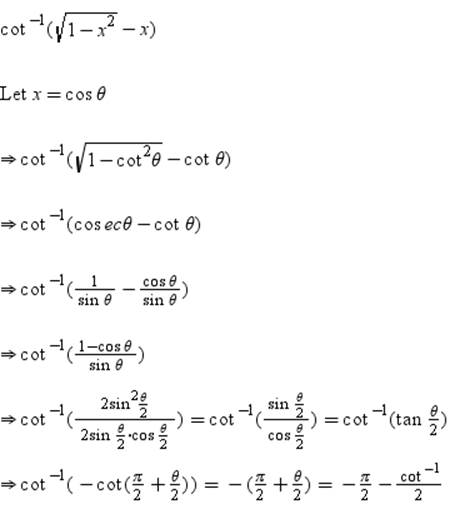INVERSE TRIGONOMETRIC FUNCTIONS

Introduction:

Every mathematical function, from the simplest to the most complex, has an inverse. In mathematics, inverse usually means opposite.

For addition, the inverse is subtraction. For multiplication, it's division. And for trigonometric functions, it's the inverse trigonometric functions.

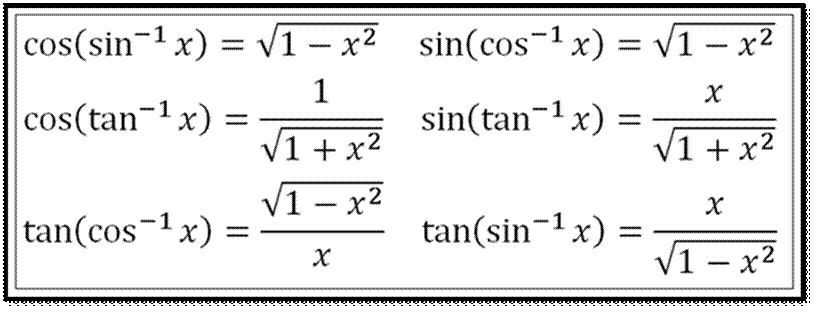
Trigonometric functions are the functions of an angle. The term function is used to describe the relationship between two sets of numbers or variables.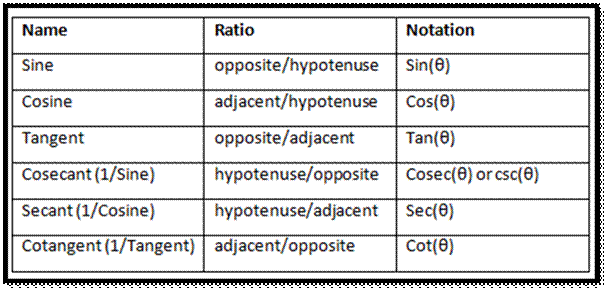

In modern mathematics, there are six basic trigonometric functions: sine, cosine, tangent, secant, cosecant, and cotangent. The inverse of these functions are inverse sine, inverse cosine, inverse tangent, inverse secant, inverse cosecant, and inverse cotangent.

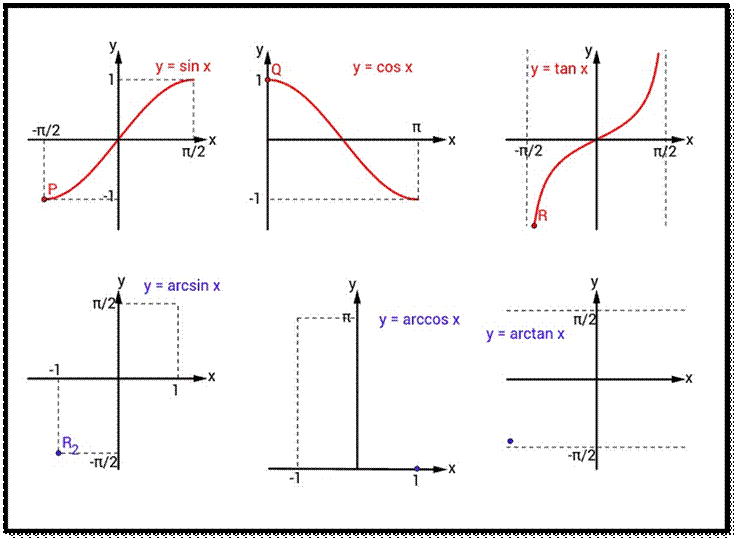
BASIC CONCEPTS :

The inverse trigonometric functions are arcus functions or anti trigonometric functions. These are the inverse functions of the trigonometric functions with suitably restricted domains. Here, we will study the inverse trigonometric formulae for the sine, cosine, tangent, cotangent, secant, and the cosecant functions, and are used to obtain an angle from any of the angle’s trigonometric ratios.

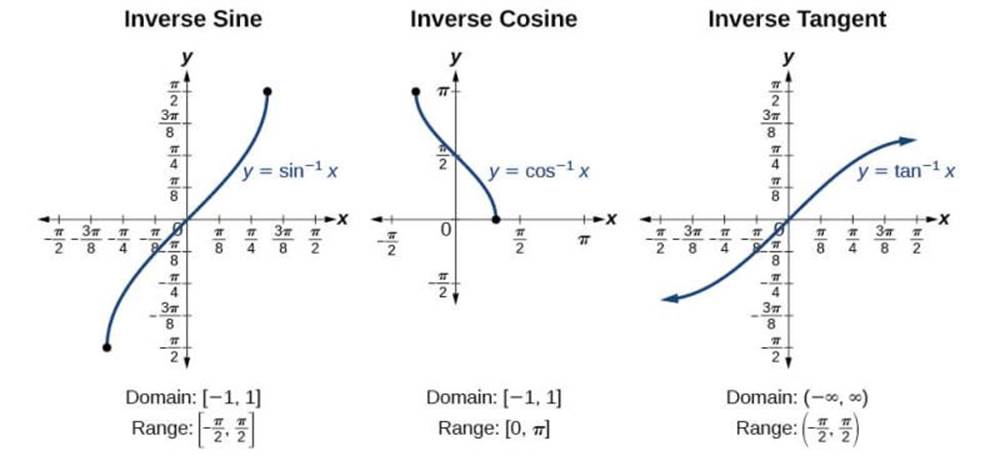
If y=f(x) and x=g(y) are two functions ,

such that f (g(y)) = y and

g (f(y)) = x, then f and y are said to be inverse of each other

i.e., g = f^-1

If y = f(x) then x = f^-1 (y)

PROPERTIES OF TRIGONOMETRIC INVERSE FUNCTIONS:

Here are the properties of the inverse trigonometric functions with proof.

PROPERTY 1 :

Ø sin^-1 (1/x) = cosec^-1x , x ≥ 1 or x ≤ -1

Ø cos^-1 (1/x) = sec^-1x , x ≥ 1 or x ≤ -1

Ø tan^-1 (1/x) = cot^-1x , x > 0

Proof :

sin^-1 (1/x) = cosec^-1x , x ≥ 1 or x ≤ -1,
Let  sin−1x=y
i.e.

x = cosec y
1x=siny
sin−1 1/x)=y
sin−1 1/x)=cosec−1x
sin−1(1x)=cosec−1x
Hence, 

sin−1 1/x=cosec−1 x where, x ≥ 1 or x ≤ -1.

PROPERTY 2 :

Ø sin^-1(-x) = – sin^-1(x),    x ∈ [-1,1]

Ø tan^-1(-x) = -tan^-1(x),   x ∈ R

Ø cosec^-1(-x) = -cosec^-1(x), |x| ≥ 1

Proof:

sin^-1(-x) = -sin^-1(x),    x ∈ [-1,1]
Let,  

sin−1(−x)=y
Then 

−x=siny
x=−siny
x=sin(−y)
sin−1=sin−1(sin(−y))
sin−1x=y
sin−1x=−sin−1(−x)
Hence,

sin−1(−x)=−sin−1 x ∈ [-1,1]

Illustrations:

1. Given, cos⁻¹⁽−3/4) = π − sin⁻¹A. Find A.

Solution:

Draw the diagram from the question statement.

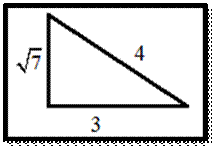
So,

cos⁻¹⁽−3/4) = π − sin⁻¹(√7/4)

Thus,

A = √7/4

2. cos⁻¹⁽¼) = sin⁻¹ √(1−1/16) = sin⁻¹(√15/4)

3. sin⁻¹⁽−½) = −cos⁻¹√(1−¼) = −cos⁻¹(√3/2)

4. sin²(tan⁻¹(¾)) = sin²(sin⁻¹(⅗)) = (⅗)² = 9/25.

5. sin⁻¹⁽sin 2π/3) = π/3

6. cos⁻¹⁽cos 4π/3) = 2π/3 sin

7. sin⁻¹⁽cos 33π/10) = sin⁻¹cos(3π + 3π/10) = ⁻¹(−sin(π/2 − 3π/10)) = −(π/2 − 3π/10) = −π/5

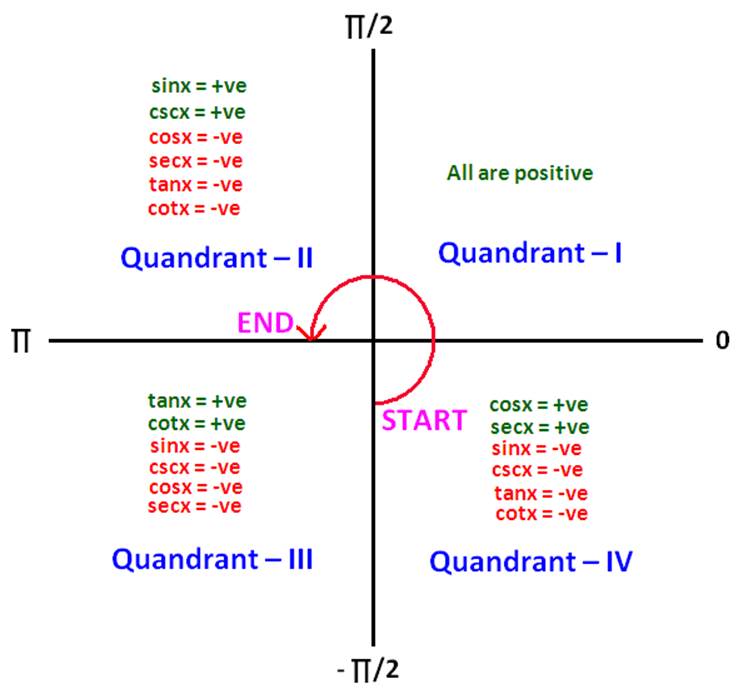
Property Set 4 : Corresponding Graphs

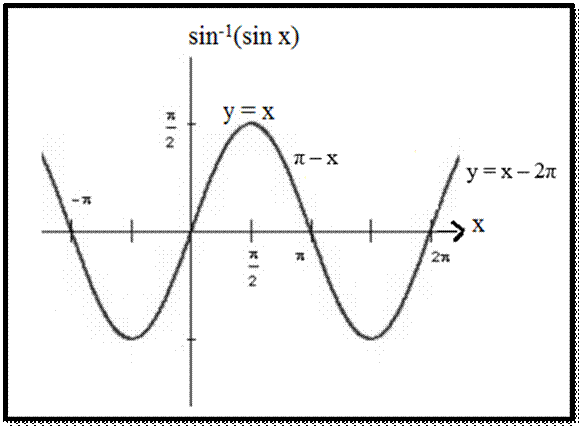
sin⁻¹⁽sin x) = −π−π, if x∈[−3π/2, −π/2]

= x, if x∈[−π/2, π/2]

= π−x, if x∈[π/2, 3π/2]

=−2π+x, if x∈[3π/2, 5π/2] And so on.

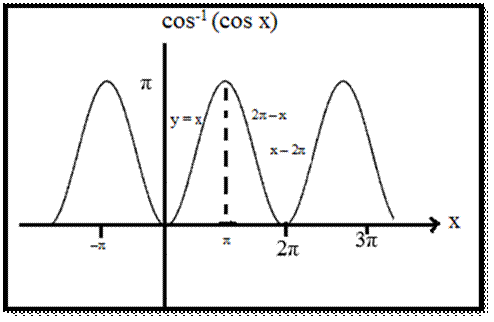
cos⁻¹⁽cos x) = 2π+x, if x∈[−2π,−π]

= −x, ∈[−π,0]

= x, ∈[0,π]

= 2π−x, ∈[π,2π]

=−2π+x, ∈[2π,3π]

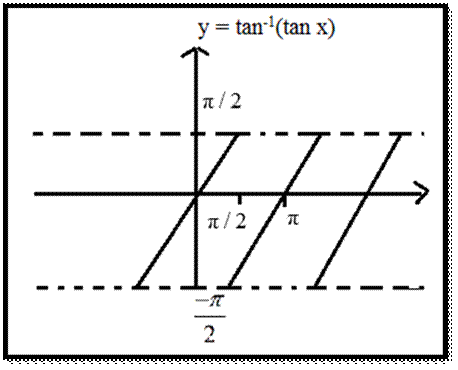
tan⁻¹⁽tan x) = π+x, x∈(−3π/2, −π/2)

= x, (−π/2, π/2)

= x−π, (π/2, 3π/2)

= x−2π, (3π/2, 5π/2)

PROPERTY 3 :

Ø cos^-1(-x) = π – cos^-1 x, x ∈ [-1,1]

Ø sec^-1(-x) = π – sec^-1x, |x| ≥ 1

Ø cot^-1(-x) = π – cot^-1x, x ∈ R

PROOF :

cos^-1(-x) = π – cos^-1 x, x ∈ [-1,1]
Let 

cos−1(−x)=y
cosy=−x x=−cosy
x=cos(π−y)
Since,  cosπ−q=−cosq
cos−1x=π−y
cos−1x=π–cos−1–x
Hence, 

cos−1−x=π–cos−1x

PROPERTY 4 :

Ø sin^-1x + cos^-1x = π/2, x ∈ [-1,1]

Ø tan^-1x + cot^-1x = π/2, x ∈ R

Ø cosec^-1x + sec^-1x = π/2, |x| ≥ 1

Proof :

sin^-1x + cos^-1x = π/2, x ∈ [-1,1]
Let 

sin−1x=y or x=siny=cos(π2−y)
cos−1x=cos−1(cos(π2−y))
cos−1x=π2−y
cos−1x=π2−sin−1x
sin−1+cos−1x=π2
Hence,

sin^-1x + cos^-1x = π/2, x ∈ [-1,1]

PROPERTY 5 :

Ø tan^-1x + tan^-1y = tan^-1((x+y)/(1-xy)), xy < 1.

Ø tan^-1x – tan^-1y = tan^-1((x-y)/(1+xy)), xy > -1.

Proof :

tan^-1x + tan^-1y = tan^-1((x+y)/(1-xy)), xy < 1.
Let

tan−1x=A
And tan−1y=B
Then, 

tanA=x
tanB=y
Now,

tan(A+B)=(tanA+tanB)/(1−tanAtanB)
tan(A+B)=x+y1−xy
tan−1(x+y1−xy)=A+B
Hence, 

tan−1(x+y1−xy)=tan−1x+tan−1y

PROPERTY 6 :

Ø 2tan^-1x = sin^-1 (2x/(1+x²)), |x| ≤ 1

Ø 2tan^-1x = cos^-1((1-x²)/(1+x²)), x ≥ 0

Ø 2tan^-1x = tan^-1(2x/(1 – x²)), -1 < x <1

Proof :

2tan^-1x = sin^-1 (2x/(1+x²)), |x| ≤ 1
Let

tan−1x=y and x=tany
Consider

RHS. sin−1(2x1+x2)
=sin−1(2tany1+tan2y)
=sin−1(sin2y)
Since,

sin2θ=2tanθ/(1+tan²θ),
=2y
=2tan−1x which is our LHS
Hence

2 tan^-1x = sin^-1 (2x/(1+x²)), |x| ≤ 1

Solved Example

Q1. Prove that “sin^-1(-x) = – sin^-1(x),    x ∈ [-1,1]”

Ans:

Let, sin−1(−x)=y
Then

−x=siny
x=−siny
x=sin(−y)
sin−1x=arcsin(sin(−y))
sin−1x=y
sin−1x=−sin−1(−x)
Hence, 

sin−1(−x)=−sin−1x, x ∈ [-1,1]

This concludes our discussion on the topic of trigonometric inverse functions.

1.Write in the simplest form: tan-1 [ cos x/1+sin x], x[-π/2, π/2]

Solution:

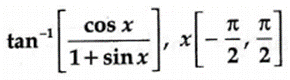
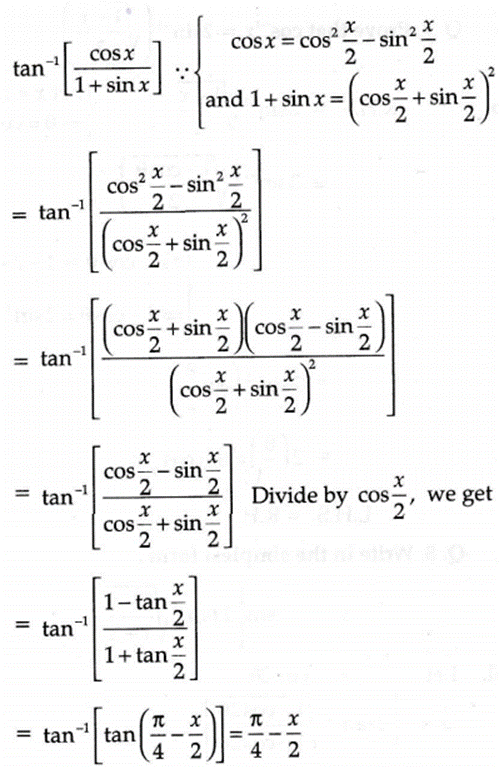
2. If tan-1 (√3) + cot-1 x = π/2, then find x.

Solution:

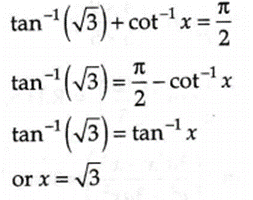
3.