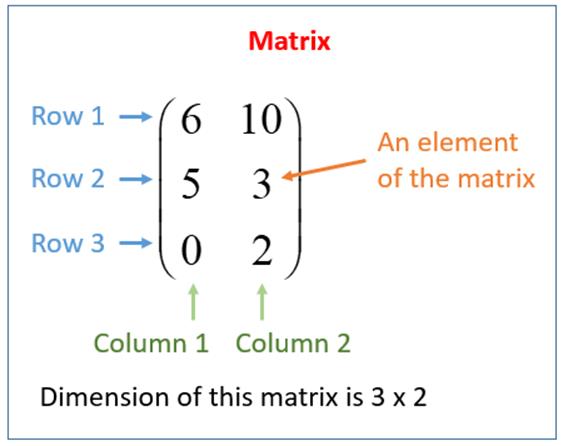
MATRIX

In mathematics, a matrix (plural matrices) is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns. Matrices are commonly written in box brackets. The horizontal and vertical lines of entries in a matrix are called rows and columns, respectively. The size of a matrix is defined by the number of rows and columns that it contains.

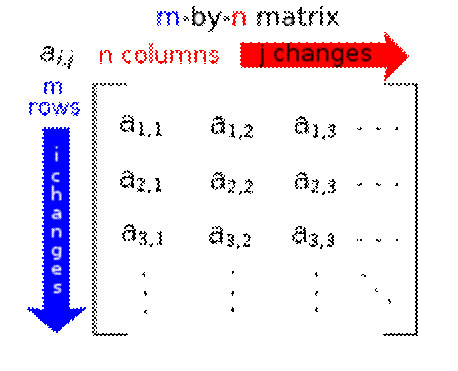
A matrix with m rows and n columns is called an m × n matrix or mm-by-nn matrix, while m and n are called its dimensions.The dimensions of the following matrix are 2×32×3 up(read “two by three”), because there are two rows and three columns.

ORDER OF A MATRIX:

A matrix having m rows and n columns is called matrix of order m x n or simply m x n matrix . In general m x n has the following form

a11	a12	......	a1n
a21	a22	......	a2n
:	:	:	:
ai1	ai2	....	ain
:	:	:	:
am1	am2	......	amn

The order of a matrix or the size of a matrix is known as the number of rows or the number of columns which are present in that matrix.

5	-2	7	9
-3	1	2	-8

The order of above matrix is 2 x 4.

Because in the above matrix there are two rows and four columns.

The element which occurs in the first row and first column = 5

The element which occurs in the first row and second column = -2

The element which occurs in the first row and third column = 7

The element which occurs in the first row and fourth column = 9

The element which occurs in the second row and first column = 3

The element which occurs in the second row and second column = 1

The element which occurs in the second row and third column = 2

The element which occurs in the second row and fourth column = -8matrix introduction

TYPES OF MATRICES:

Different types of Matrices and their forms are used for solving numerous problems.

1) ROW MATRIX:

A row matrix has only one row but any number of columns. A matrix is said to be a row matrix if it has only one row.

For example,

A=[−1/2√523]

Is A Row matrix of order 1 × 4.

In general, A = [a_ij]_{1 × n} is a row matrix of order 1 × n.

2) Column Matrix :

A column matrix has only one column but any number of rows. A matrix is said to be a column matrix if it has only one column.

For example,

3) SQUARE MATRIX :

A square matrix has the number of columns equal to the number of rows. A matrix in which the number of rows is equal to the number of columns is said to be a square matrix. 

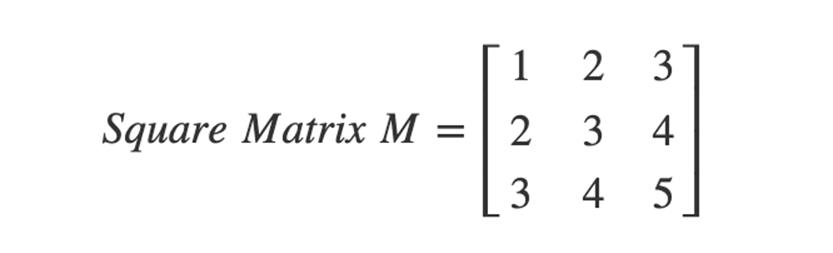
4) RECTANGULAR MATRIX :

A matrix is said to be a rectangular matrix if the number of rows is not equal to the number of columns. For example, 

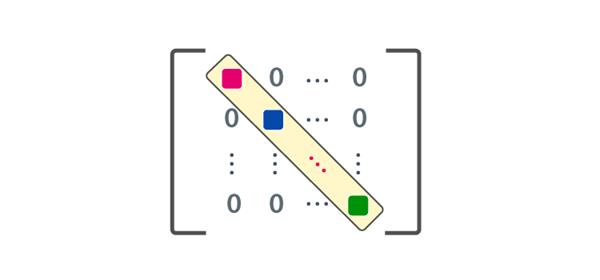
5) DIAGONAL MATRIX :

A square matrix B = [bij] m × m is said to be a diagonal matrix if all its non-diagonal elements are zero, that is a matrix B =[b_ij]_m×m is said to be a diagonal matrix if b_ij = 0, when i ≠ j. 

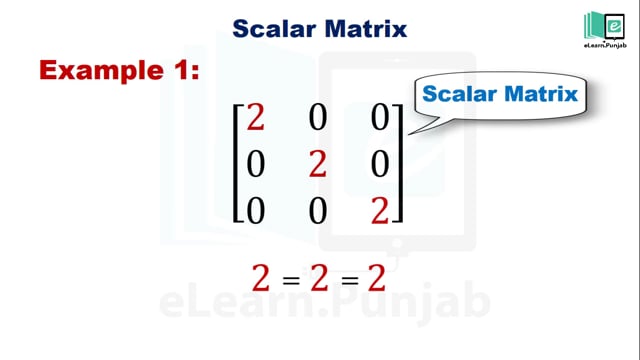
6) SCALAR MATRIX :

A diagonal matrix is said to be a scalar matrix if all the elements in its principal diagonal are equal to some non-zero constant. A diagonal matrix is said to be a scalar matrix if its diagonal elements are equal, that is, a square matrix B = [b_ij]_{n × n} is said to be a scalar matrix if

· b_ij = 0, when i ≠ j

· b_ij = k, when i = j, for some constant k.

7) ZERO OR NULL MATRIX :

A matrix is said to be zero matrix or null matrix if all its elements are zero.
For Example,

8) UNIT OR IDENTITY MATRIX :

If a square matrix has all elements 0 and each diagonal elements are non-zero, it is called identity matrix and denoted by I.
Equal Matrices:

Two matrices are said to be equal if they are of the same order and if their corresponding elements are equal to the square matrix A = [a_ij]_{n × n} is an identity matrix if

· a_ij = 1 if i = j

· a_ij = 0 if i ≠ j

We denote the identity matrix of order n by I_n. When the order is clear from the context, we simply write it as I. For example,

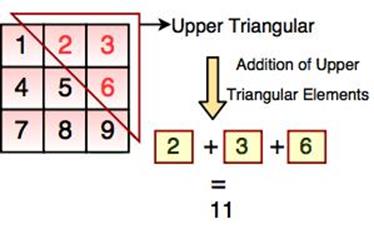
9) UPPER TRIANGULAR MATRIX :

A square matrix in which all the elements below the diagonal are zero is known as the upper triangular matrix. For example, 

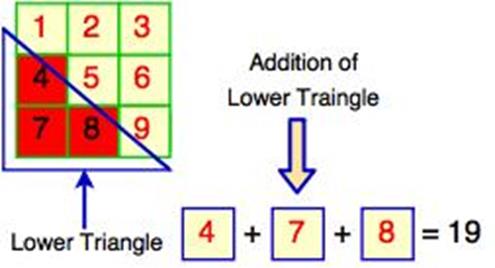
10) LOWER TRIANGULAR MATRIX :

A square matrix in which all the elements above the diagonal are zero is known as the upper triangular matrix. For example, 

DEFINITION OF EQUALITY OF MATRICES:

Two matrices A and B are known as equality of matrices if both matrices is having same order.  If two matrices are equal then its corresponding terms will be equal. Based on these property let us look into the following examples to get more practice in this topic.

Example 1:

If the following two matrices are equal then find the values of x,y,w and z.

x	y
w	z

=

1	5
7	9

Solution:

We can say the above two matrices are equal because they are having same order (2 x 2).

Corresponding term of  x is 1

Corresponding term of  y is 5

Corresponding term of  w is 7

Corresponding term of  z is 9

Therefore the values of x = 1, y = 5, w = 7 and z = 9

---

Example 2:

If the following two matrices are equal then find the values of p,q,r and t.

2p	5p+q
3t	5t+r

=

10	17
9	15

Solution:

We can say the above two matrices are equal because they are having same order (2 x 2).

Corresponding term of  2p is 10

Corresponding term of  5p + q is 17

Corresponding term of  3t is 9

Corresponding term of  5t + r is 15

2 p = 10    p = 10/2    p = 5

5p + q = 17 5(5) + p = 17  25 + p = 17     p = 17 - 25     p = -8

3t = 9   t = 9/3   t = 3

5t + r = 15 5 (3) + r = 15  15 + r = 15         r = 15 - 15          r = 0

Therefore values of p = 5, q = -8, t = 3 and r = 0 equality of matrices

OPERATIONS ON MATRICES :

In this page operations on matrices we are going to see how to add,subtract and multiply two matrices.

Addition of two matrices:

Two and more matrices can be added if and only if they are having same order. If the order those matrices are not same then we cannot add those matrices.

Example 1:

Find the sum of the following matrices

A =

0	2	7
-3	2	11

B =

-3	1	13
8	-7	0

Solution:

A+B=

0	2	7
-3	2	11

+

-3	1	13
8	-7	0

The given two matrices are in the same order, so we may add these matrices. For that we have to combine the corresponding terms.

  =

0-3	2+1	7+13
-3+8	2-7	11+0

  =

-3	3	20
5	-5	11

Subtraction of two matrices:

Two and more matrices can be subtracted if and only if they are having same order. If the order those matrices are not same then we cannot subtract those matrices.

Example 2:

Subtract the following matrices

A =

5	-1	3
8	6	-3

B =

-4	0	-5
7	-8	11

Solution:

A-B=

5	-1	3
8	6	-3

-

-4	0	-5
7	-8	11

The given two matrices are in the same order, so we shall subtract these matrices. For that we have to combine the corresponding terms.

  =

5-(-4)	-1-0	3-(-5)
8-7	6-(-8)	-3-11

  =

5+4	-1	3+5
8-7	6+8	-3-11

  =

9	-1	8
1	14	-14

Multiplication of two matrices:

The product of matrix AB is determined by myltiplying every row matrix of A multiplying by the column matrix of B.

Example 3:

Multiply the following matrices

A =

5	-1
8	6

B =

-4	0
7	-8

Every column of the second is to be multiplied by every row of the first matrix.

AB=

5	-1
8	6

x

-4	0
7	-8

=

5

-1

x

-4

7

5

-1

x

0

-8

8

6

x

-4

7

8

6

x

0

-8

=

(-20-7)	(0+8)
(-32+42)	(0-48)

AB=

-27	8
10	-48

These are the properties of the topic operations on matrices.opertion.

PROPERTIES OF MATRICES.:

In this page we are going to algebraic properties of matrices we are going to see some properties in the concept matrix.

Matrix Addition is Commutative:

If A and B are any two matrices of the same order then A+B = B+A. This property is known as commutative property of matrix addition.

A =

0	7
-3	11

B =

-3	1
-7	0

Now let us find A + B

A+B=

0	7
-3	11

+

-3	1
-7	0

A+B=

0+(-3)	7+1
-3+(-7)	11+0

A+B=

-3	8
-10	11

Now let us find B + A

B+A=

-3	1
-7	0

+

0	7
-3	11

B+A=

(-3)+0	1+7
(-7)+(-3)	0+11

B+A=

-3	8
-10	11

Matrix Addition is Associative:

If A,B and C are any three matrices of same order then A+(B+C) = (A+B)+C. This is the property of matrix addition.

A =

1	2
3	1

B =

2	3
7	6

C =

5	2
3	1

Now let us find B + C

B+C=

2	3
7	6

+

5	2
3	1

B+C=

(2+5)	(3+2)
(7+3)	(6+1)

B+C=

7	5
10	7

Now we have to find A + (B+C)

A+(B+C)=

1	2
3	1

+

7	5
10	7

A+(B+C)=

(1+7)	(2+5)
(3+10)	(1+7)

A+(B+C)=

8	7
13	8

Now let us find A + B

A+B=

1	2
3	1

+

2	3
7	6

Now we have to add corresponding terms

A+B=

(1+2)	(2+3)
(3+7)	(1+6)

A+B=

3	5
10	7

Now we have to add A+B with C.

(A+B)+C=

3	5
10	7

+

5	2
3	1

A+(B+C)=

(3+5)	(5+2)
(10+3)	(7+1)

A+(B+C)=

8	7
13	8

Additive Identity:

Let A be any matrix then A + O = 0 + A = A. This property i called additive property of matrix identity.

A =

1	2
3	5

O =

0	0
0	0

To check this,first we have to add A + O

A+O=

1	2
3	5

+

0	0
0	0

A+O=

(1+0)	(2+0)
(3+0)	(5+0)

A+O=

1	2
3	5

Now we have to add O+A

O+A=

0	0
0	0

+

1	2
3	5

O+A=

(0+1)	(0+2)
(0+3)	(0+5)

A+O=

1	2
3	5

Additive Inverse:

Let A be any matrix then A + (-A) = (-A) + A = o. This property is called as additive inverse. The zero matrix is also known as identity element with respect to matrix addition.

These are the properties in addition in the topic algebraic properties of matrices.

MULTIPLICATION PROPERTIES OF MATRICES

The following are the multiplication properties of matrices :

1. Matrix Multiplication is not Commutative :

For any two matrices A and B,

AB  ≠  BA

2. Associative Property :

For any three matrices A, B and C,

A(BC)  =  (AB)C

. 3.Distributive Property :

For any three matrices A, B and C.

A(B + C)  =  AB + AC

(A + B)C  =  AC + AB

3. Identity Property :

For any matrix A and the identity matrix I, 

AI  =  IA  =  A

Matrix Multiplication is not Commutative - Example

A  =  

1	2
5	3

B  =  

2	5
7	3

Find the product of A and B :

AB  =  

1	2
5	3

x

2	5
7	3

=

1

2

x

2

7

1

2

x

5

3

5

3

x

2

7

5

3

x

5

3

=

(2+14)	(5+6)
(10+21)	(25+9)

AB  =  

16	11
31	34

Find the product of B and A :

BA  =  

2	5
7	3

x

1	2
5	3

=

2

5

x

1

5

2

5

x

2

3

7

3

x

1

5

7

3

x

2

3

=

(2+25)	(4+15)
(7+15)	(14+9)

BA  =  

27	19
22	23

Therefore, 

AB  ≠  BA

Associative Property - Example

A =

1	2
5	3

B =

2	5
7	3

C =

1	3
5	1

Find the product of B and C :

BC  =  

2	5
7	3

x

1	3
5	1

=

2

5

x

1

5

2

5

x

3

1

7

3

x

1

5

7

3

x

3

1

=

(2+25)	(6+5)
(7+15)	(21+3)

BC  =  

27	11
22	24

Find the product of A and (BC) :

A(BC)  =  

1	2
5	3

x

27	11
22	24

=

(27+44)	(11+48)
(135+66)	(55+72)

A(BC)  =  

71	59
201	127

Find the product of A and B :

AB  =  

1	2
5	3

x

2	5
7	3

=

1

2

x

2

7

1

2

x

5

3

5

3

x

2

7

5

3

x

5

3

=

(2+14)	(5+6)
(10+21)	(25+9)

AB  =  

16	11
31	34

Find the product of (AB) and C :

(AB)C  =  

16	11
31	34

x

1	3
5	1

=

16

11

x

1

5

16

11

x

3

1

31

34

x

1

5

31

34

x

3

1

=

(16+55)	(48+11)
(31+170)	(93+34)

(AB)C  =  

71	59
201	127

Therefore, 

A(BC)  =  (AB)C

Distributive Property - Example

A =

1	2
5	3

B =

2	5
7	3

C =

1	3
5	1

Find the addition of B and C :

B+C  =  

2	5
7	3

+

1	3
5	1

=

3	8
12	4

Find the product of A and (B + C) :

A(B + C)  =  

1	2
5	3

x

3	8
12	4

=

1

2

x

3

12

1

2

x

8

4

5

3

x

3

12

5

3

x

8

4

=

(3+24)	(8+8)
(15+36)	(40+12)

A(B + C)  =  

27	16
51	52

Find the product of A and B :

AB  =  

1	2
5	3

x

2	5
7	3

=

1

2

x

2

7

1

2

x

5

3

5

3

x

2

7

5

3

x

5

3

=

(2+14)	(5+6)
(10+21)	(25+9)

AB  =  

16	11
31	34

Find the product of A and C :

AC  =  

1	2
5	3

x

1	3
5	1

=

1

2

x

1

5

1

2

x

3

1

5

3

x

1

5

5

3

x

3

1

=

(1+10)	(3+2)
(5+15)	(15+3)

AC  =  

11	5
20	18

Find the addition of AB and AC :

AB + AC  =  

16	11
31	34

+

11	5
20	18

    =  

(16+11)	(11+5)
(31+20)	(34+18)

AB + AC  =  

27	16
51	52

Therefore,

A(B + C)  =  AB + AC

Identity Property – Example :

A =

1	2
5	3

I =

1	0
0	1

Find the product of A and I :

AI  =  

1	2
5	3

x

1	0
0	1

=

1

2

x

1

0

1

2

x

0

1

5

3

x

1

0

5

3

x

0

1

=

(1+0)	(0+2)
(5+0)	(0+3)

AI  =  

1	2
5	3

Find the product of I and A :

AI  =  

1	0
0	1

x

1	2
5	3

=

1

0

x

1

5

1

0

x

2

3

=

0

1

x

1

5

0

1

x

2

3

=

(1+0)	(2+0)
(0+5)	(0+3)

IA  =  

1	2
5	3

Therefore,

AI  =  IA

INVERSE OF A MATRIX :

If A is a non-singular matrix,there exists an in= (A⁻¹)^T

These are the properties in the topic inverse of a matrix. In this page we are going to see how to find inverse of a matrix.

1) Reversal law for inverse

If A and B are any two non singular matrices of the same order,then AB is also non singular and (AB)⁻¹ = B⁻¹ A⁻¹ the inverse of a product is the product of the inverses taken in the reverse order.

2) Reversal law of Transposes

If A and B are matrices comfortable to multiplication,then (AB)^T = B^T A^T

3) Inverse law

For any non singular matrix A. (A^T)⁻¹

Definition:

verse which is given by

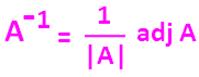
Example 1:

Find the inverse of the following matrix

3	1	-1
2	-2	0
1	2	-1

|A| = 3 [2-0] - 1 [-2-0] -1 [4-(-2)]

      = 3 [2] - 1 [-2] -1 [4+2]

      = 6 +2 -1 [6]

      = 6 +2 -6

|A| = 2 ≠ 0

Since A is a non singular matrix. A⁻¹ exists.

minor of 3

=

-2	0
2	-1

   = [2-0]

   =  2

minor of 1

=

2	0
1	-1

   = [-2-0]

   =  -2

minor of -1

=

2	-2
1	2

   = [4-(-2)]

   = [4+2]

   =  6

minor of 2

=

1	-1
2	-1

   = [-1-(-2)]

   = [-1+2]

   =  1

minor of -2

=

3	-1
1	-1

   = [-3-(-1)]

   = [-3+1]

   =  -2

minor of 0

=

3	1
1	2

   = [6-1]

   =  5

minor of 1

=

1	-1
-2	0

   = [0-2]

   =  -2

minor of 2

=

3	-1
2	0

   = [0-(-2)]

   =  2

minor of -1

=

3	1
2	-2

   = [-6-2]

   =  -8

minor matrix   =

2	-2	6
1	-2	5
-2	2	-8

cofactor matrix =

2	2	6
-1	-2	-5
-2	-2	-8

Adjoint matrix =

2	-1	-2
2	-2	-2
6	-5	-8

 A⁻¹ =1/2

2	-1	-2
2	-2	-2
6	-5	-8

Example 2:

Find the inverse of the following matrix

3	4	1
0	-1	2
5	-2	6

|A| = 3 [-6-(-4)] - 4 [0-10] +1 [0-(-5)]

      = 3 [-6+4] - 4 [-10] +1 [5]

      = 3 [-2] + 40 + 5

      = -6 + 40 + 5

      = -6 + 45

      = 39

|A| = 39 ≠ 0

Since A is a non singular matrix. A⁻¹ exists.

minor of 3

=

-1	2
-2	6

   = [-6-(-4)]

   = (-6+4)

   = -2

minor of 4

=

0	2
5	6

   =  [0-10]

   =  (-10)

   = -10

minor of 1

=

0	-1
5	-2

   =  [0-(-5)]

   =  [0+5]            

   =  5

minor of 0

=

4	1
-2	6

   = [24-(-2)]

   = [24+2]

   =  26

minor of -1

=

3	1
5	6

   = [18-5]

   =  13

minor of 2

=

3	4
5	-2

   = [-6-20]

   =  -26

minor of 5

=

4	1
-1	2

   =  [8-(-1)]

   =  (8+1)

   =  9

minor of -2

=

3	1
0	2

   =  [6-0]

   =  6

minor of 6

=

3	4
0	-1

   =  [-3-0]

   =  -3

minor matrix

-2	-10	5
26	13	-26
9	6	-3

Co-factormatrix

-2	10	5
-26	13	26
9	-6	-3

Ad-joint of matrix (adj A)

-2	-26	9
10	13	-6
5	26	-3

 A⁻¹=1/39

-2	-26	9
10	13	-6
5	26	-3

These are the examples in the page inverse of a matrix.

ELEMENTARY MATRIX OPERATIONS

Elementary matrix operations play an important role in many matrix algebra applications, such as finding the inverse of a matrix and solving simultaneous linear equations.

ELEMENTARY OPERATIONS :

There are three kinds of elementary matrix operations.

Ø Interchange two rows (or columns).

Ø Multiply each element in a row (or column) by a non-zero number.

Ø Multiply a row (or column) by a non-zero number and add the result to another row (or column).

When these operations are performed on rows, they are called elementary row operations; and when they are performed on columns, they are called elementary column operations.

Elementary Operation Notation

In many references, you will encounter a compact notation to describe elementary operations. That notation is shown below.

Operation description	Notation
Row operations
1. Interchange rows i and j	Ri <--> Rj
2. Multiply row i by s, where s ≠ 0	sRi --> Ri
3. Add s times row i to row j	sRi + Rj --> Rj
Column operations
1. Interchange columns i and j	Ci <--> Cj
2. Multiply column i by s, where s ≠ 0	sCi --> Ci
3. Add s times column i to column j	sCi + Cj --> Cj

Elementary Operators :

Each type of elementary operation may be performed by matrix multiplication, using square matrices called elementary operators.

For example,

suppose you want to interchange rows 1 and 2 of Matrix A. To accomplish this, you could premultiply A by E to produce B, as shown below.

R₁ <--> R₂    =    

0	1
1	0

1	3	5
2	4	6

E

A

R₁ <--> R₂    =    

0 + 2	0 + 4	0 + 6
0 + 1	0 + 3	0 + 5

R₁ <--> R₂    =    

2	4	6
1	3	5

    =    B

Here, E is an elementary operator. It operates on A to produce the desired interchanged rows in B. What we would like to know, of course, is how to find E. Read on.

HOW TO PERFORM ELEMENTARY ROW OPERATIONS :

To perform an elementary row operation on a A, an r x c matrix, take the following steps.

1. To find E, the elementary row operator, apply the operation to an r x r identity matrix.

2. To carry out the elementary row operation, premultiply A by E.

We illustrate this process below for each of the three types of elementary row operations.

§ Interchange two rows. Suppose we want to interchange the second and third rows of A, a 3 x 2 matrix. To create the elementary row operator E, we interchange the second and third rows of the identity matrix I₃.

1	0	0
0	1	0
0	0	1

⇒

1	0	0
0	0	1
0	1	0

I₃

E

§ Then, to interchange the second and third rows of A, we premultiply A by E, as shown below.

R₂ <--> R₃  =  

1	0	0
0	0	1
0	1	0

0	1
2	3
4	5

E

A

R₂ <--> R₃ = 

1*0 + 0*2 + 0*4	1*1 + 0*3 + 0*5
0*0 + 0*2 + 1*4	0*1 + 0*3 + 1*5
0*0 + 1*2 + 0*4	0*1 + 1*3 + 0*5

R₂ <--> R₃  =  

0	1
4	5
2	3

§ Multiply a row by a number. Suppose we want to multiply each element in the second row of Matrix A by 7. Assume A is a 2 x 3 matrix. To create the elementary row operator E, we multiply each element in the second row of the identity matrix I₂ by 7.

1	0
0	1

⇒

1	0
0	7

I₂

E

§ Then, to multiply each element in the second row of A by 7, we premultiply A by E.

7R₂ --> R₂  =  

1	0
0	7

0	1	2
3	4	5

E

A

7R₂ --> R₂ = 

1*0 + 0*3	1*1 + 0*4	1*2 + 0*5
0*0 + 7*3	0*1 + 7*4	0*2 + 7*5

7R₂ --> R₂  =  

0	1	2
21	28	35

§ Multiply a row and add it to another row. Assume A is a 2 x 2 matrix. Suppose we want to multiply each element in the first row of A by 3; and we want to add that result to the second row of A. For this operation, creating the elementary row operator is a two-step process. First, we multiply each element in the first row of the identity matrix I₂ by 3. Next, we add the result of that multiplication to the second row of I₂ to produce E.

1	0
0	1

⇒

1	0
0 + 3*1	1 + 3*0

⇒

1	0
3	1

I₂

E

§ Then, to multiply each element in the first row of A by 3 and add that result to the second row, we premultiply A by E.

3R₁  +  R₂ -->  R₂  =  

1	0
3	1

0	1
2	3

E

A

3R₁  +  R₂ -->  R₂  =  

1*0 + 0*2	1*1 + 0*3
3*0 + 1*2	3*1 + 1*3

3R₁  +  R₂ -->  R₂  =  

0	1
2	6

How to Perform Elementary Column Operations

To perform an elementary column operation on A, an r x c matrix, take the following steps.

1. To find E, the elementary column operator, apply the operation to an c x c identity matrix.

2. To carry out the elementary column operation, postmultiply A by E.

Let's work through an elementary column operation to illustrate the process. For example, suppose we want to interchange the first and second columns of A, a 3 x 2 matrix. To create the elementary column operator E, we interchange the first and second columns of the identity matrix I₂.

1	0
0	1

⇒

0	1
1	0

I₂

E

Then, to interchange the first and second columns of A, we postmultiply A by E, as shown below.

C₁ <--> C₂    =    

0	1
2	3
4	5

0	1
1	0

A

E

C₁ <--> C₂  =  

0*0 + 1*1	0*1 + 1*0
2*0 + 3*1	2*1 + 3*0
4*0 + 5*1	4*1 + 5*0

C₁ <--> C₂  =  

1	0
3	2
5	4

Note that the process for performing an elementary column operation on an r x c matrix is very similar to the process for performing an elementary row operation. The main differences are:

• To operate on the r x c matrix A, the row operator E is created from an r x r identity matrix; whereas the column operator E is created from an c x c identity matrix.
  
  
• To perform a row operation, A is premultiplied by E; whereas to perform a column operation, A is postmultiplied by

MATRIX INVERSION :

Suppose A is an n x n matrix. The inverse of A is another n x n matrix, denoted A^-1, that satisfies the following conditions.

AA^-1 = A^-1A = I_n

where I_n is the identity matrix. Below, with an example, we illustrate the relationship between a matrix and its inverse.

2	1
3	4

0.8	-0.2
-0.6	0.4

    =    

1	0
0	1

A

A^-1

I

0.8	-0.2
-0.6	0.4

2	1
3	4

    =    

1	0
0	1

A^-1

A

I

Not every square matrix has an inverse; but if a matrix does have an inverse, it is unique.

Does the Inverse Exist?

There are two ways to determine whether the inverse of a square matrix exists.

• Determine its rank. The rank of a matrix is a unique number associated with a square matrix. If the rank of an n x n matrix is less than n, the matrix does not have an inverse. We showed how to determine matrix rank previously.
• Compute its determinant. The determinant is another unique number associated with a square matrix. When the determinant for a square matrix is equal to zero, the inverse for that matrix does not exist. We showed how to find the determinant of a matrix previously.

A square matrix that has an inverse is said to be nonsingular or invertible; a square matrix that does not have an inverse is said to be singular.

How to Find the Inverse of a Matrix: Special Cases

In this lesson, we show how to find the inverse of a matrix for two special cases: a diagonal matrix and a 2 x 2 matrix. In the next lesson, we show how to find the inverse for any matrix.

HOW TO FIND THE INVERSE OF A DIAGONAL MATRIX :

A diagonal matrix matrix is a special kind of symmetric matrix. It is a symmetric matrix with zeros in the off-diagonal elements. Two diagonal matrices are shown below.

A =    

1	0
0	3

B =    

5	0	0
0	3	0
0	0	1

Note that the diagonal of a matrix refers to the elements that run from the upper left corner to the lower right corner.

The inverse of a diagonal matrix is obtained by replacing each element in the diagonal with its reciprocal, as illustrated below for matrix C.

C =    

2	0
0	4

C^-1 =    

1/2	0
0	1/4

It is easy to confirm that C^-1 is the inverse of C, since

CC^-1 = C^-1C = I

where I is the identity matrix.

This approach will work for any diagonal matrix, as long as none of the diagonal elements is equal to zero. If any of the diagonal elements are equal to zero, the matrix will be less than full rank, and the matrix will not have an inverse.

How to Find the Inverse of a 2 x 2 Matrix ?

Suppose A is a nonsingular matrix 2 x 2 matrix. Then, the inverse of A can be computed from A, as shown below.

A11	A12
A21	A22

A22/|A|	-A12/|A|
-A21/|A|	A11/|A|

A

A^-1

where the determinant of A is |A| = A₁₁A₂₂ - A₁₂A₂₁ .

To illustrate how this works, let's find the inverse of matrix B, which appears below.

B =    

2	1
4	4

First, let's compute the determinant of matrix B.

|B| = B₁₁B₂₂ - B₁₂B₂₁

= 2*4 - 1*4

= 8 - 4

= 4

Then, we can find the inverse, as shown below.

B^-1 =    

B22/|B|	-B12/|B|
-B21/|B|	B11/|B|

B^-1 =    

4/4	-1/4
-4/4	2/4

    =    

1	-1/4
-1	1/2

Warning: If the determinant of a matrix is equal to zero, then the matrix does not have an inverse.

Test Your Understanding

Problem 1

Find the inverse of matrix A, shown below.

A =    

2	0
0	0

Solution

This was sort of a trick question. Matrix A is a diagonal matrix with a zero element in its diagonal.

Therefore, matrix A is singular, and does not have an inverse.

Problem 2

Find the inverse of matrix A, shown below.

A =    

2	0
0	8

Solution

The inverse of a diagonal matrix is obtained by replacing each element in the diagonal with its reciprocal, as shown below.

A^-1 =    

1/2	0
0	1/8

Problem 3

Find the inverse of matrix A, shown below.

A =    

3	1
9	4

Solution

First, let's compute the determinant of matrix A.

|A| = A₁₁A₂₂ - A₁₂A₂₁

 = 3*4 - 1*9

= 12 – 9

= 3

Then, we can find the inverse, as shown below.

A^-1 =    

A22/|A|	-A12/|A|
-A21/|A|	A11/|A|

A^-1 =    

4/3	-1/3
-9/3	3/3

  =    

4/3	-1/3
-3	1