Determinant

Definition:

· The determinant of a matrix is a special number that can be calculated from a square matrix.

· It is denoted by det (A) or |A| .

· Every square matrix A of the order n, can associate a number called determinants of the square matrix A.

Determinant of the order one (1×1):

· Consider a matrix A of order 1, then the determinant of the matrix is equal to

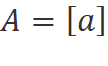
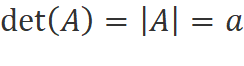
Determinant of the order Two (2×2):

· If the order of the matrix is 2, then the determinants is defined matrix A, where A is,

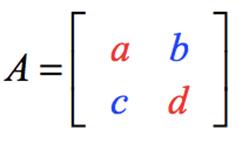
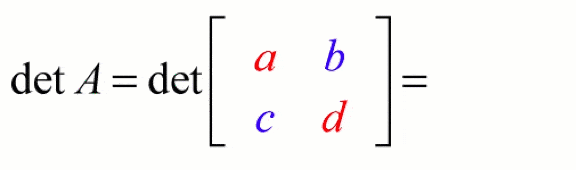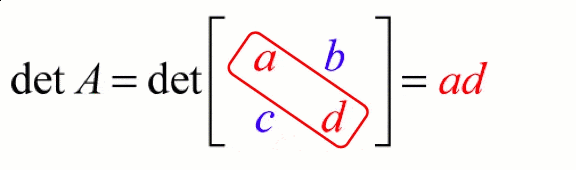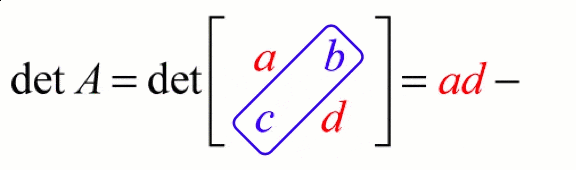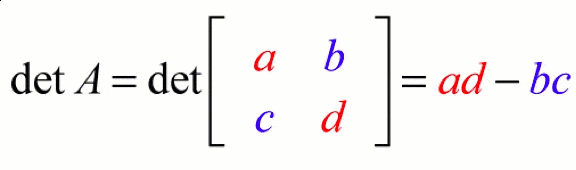
· Example on finding a 2x2 matrix determinant

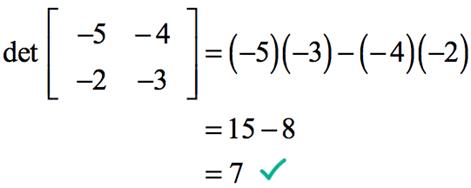
Determinant of the Order Three (3×3):

· Suppose a matrix A of order three is given as,

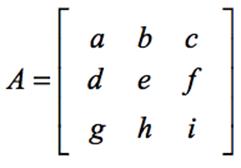
· Then the determinant for a 3×3 matrix is given by,

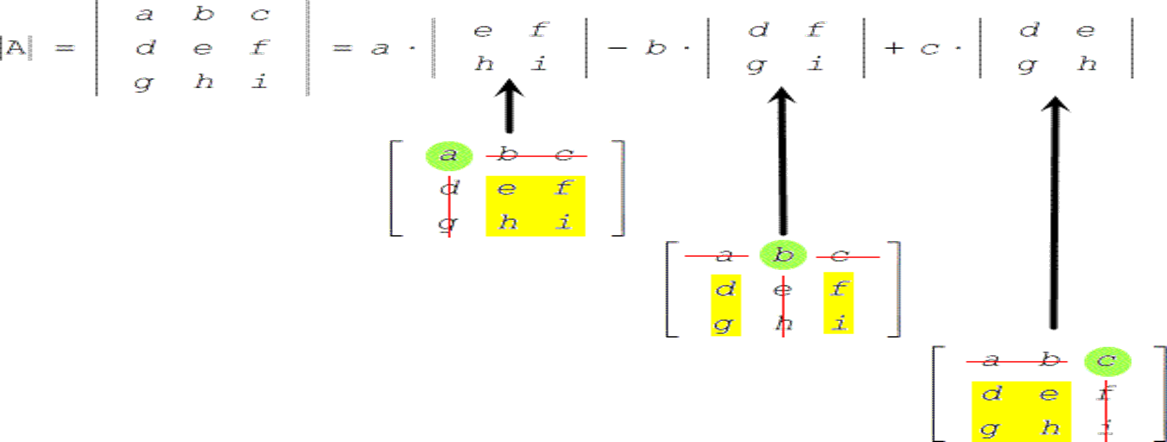
Properties of Determinant:

· Property 1

· The value of the determinant remains unchanged if both rows and columns are interchanged.

· Verification,

· Property 2

· If any two rows (or columns) of a determinant are interchanged, then the sign of determinant changes.

· Verification

· Property 3:

· If any two rows (or columns) of a determinant are identical (all corresponding elements are same), then the value of the determinant is zero.

· Verification,

· Property 4:

· If each element of a row (or a column) of a determinant is multiplied by a constant k, then its value gets multiplied by k.

· Verification,

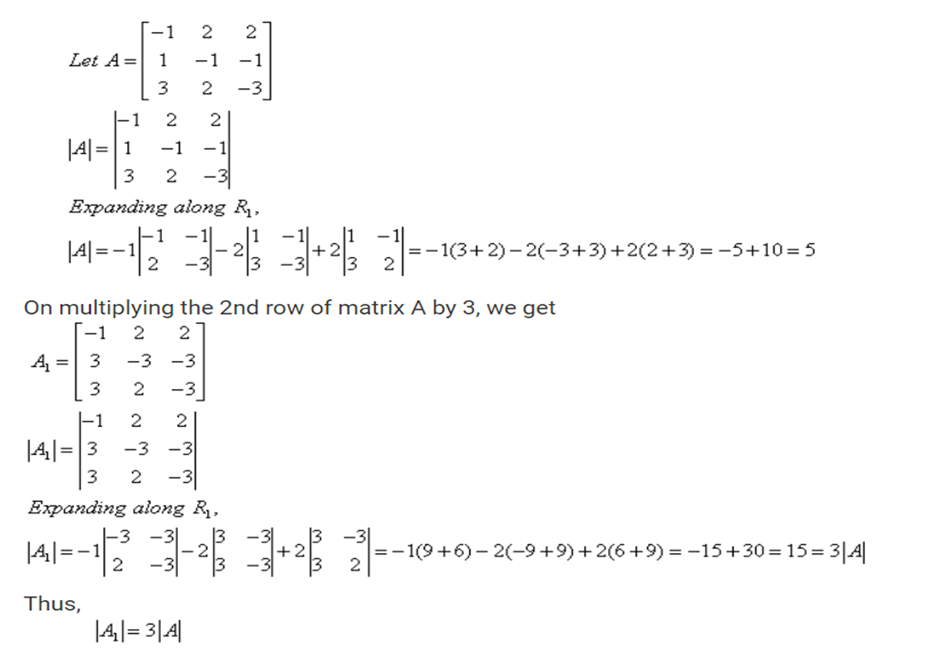
· By this property, we can take out any common factor from any one row or any one column of a given determinant.

· If corresponding elements of any two rows (or columns) of a determinant are proportional (in the same ratio), then its value is zero.

· Property 5:

· If some or all elements of a row or column of a determinant are expressed as the sum of two (or more) terms, then the determinant can be expressed as the sum of two (or more) determinants.

· Property 6:

· If the equimultiples of corresponding elements of other rows (or columns) are added to every element of any row or column of a determinant, then the value of determinant remains the same, i.e., the value of determinant remains same if we apply the operation

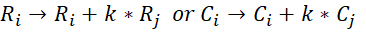
· If more than one operation like Ri → Ri+ kRj is done in one step, care should be taken to see that a row that is affected in one operation should not be used inanother operation. A similar remark applies to column operations.

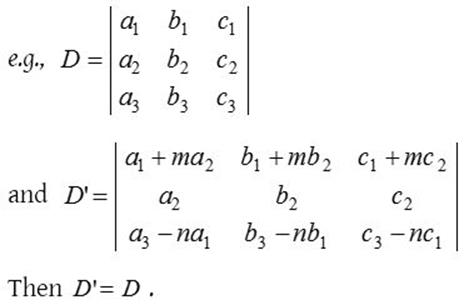
Area of Triangle Using Determinant:

· If a triangle whose vertices are given by

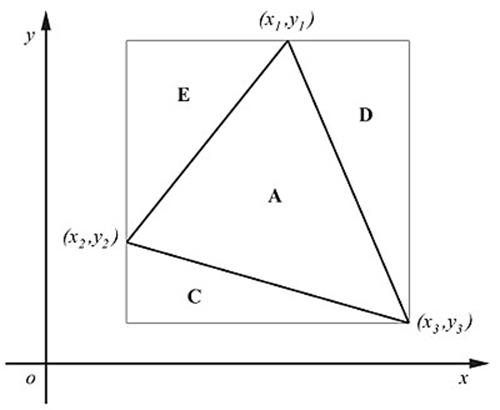
· Then the area of triangle will be given by,

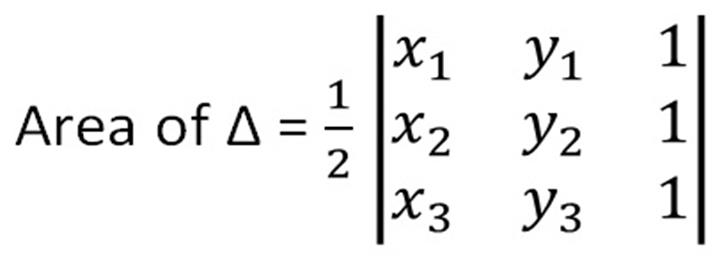
· Examples

Minors and Cofactors:

· The Minor of the element at the row is the determinant obtained by deleting the row and the column

· The Cofactor of this element is .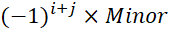

· Finding Minor and cofactor for 2x2 determinant,

· Let the determinant be given as,

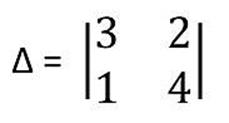
· Minors will be given as

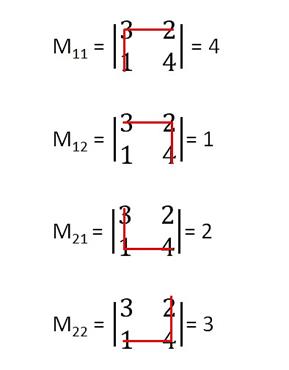
· Cofactor will be given as

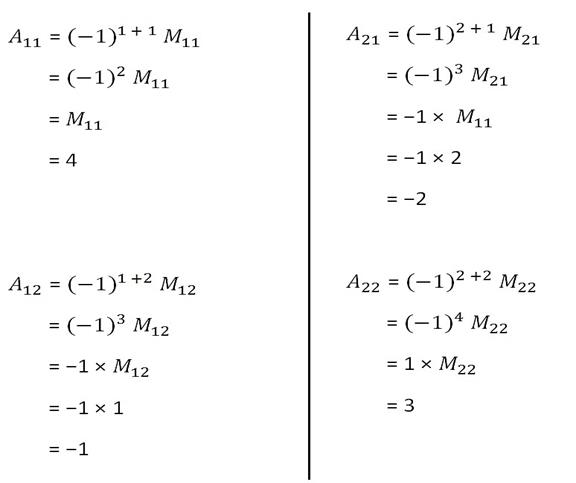
· Finding Minor and cofactor for 3x3 determinant

· Minors will be,

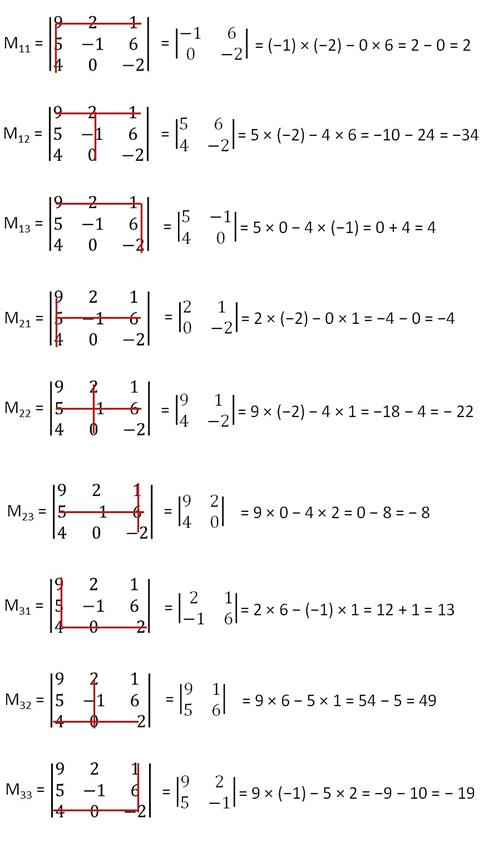
· Cofactors will be,

· Use of cofactor,

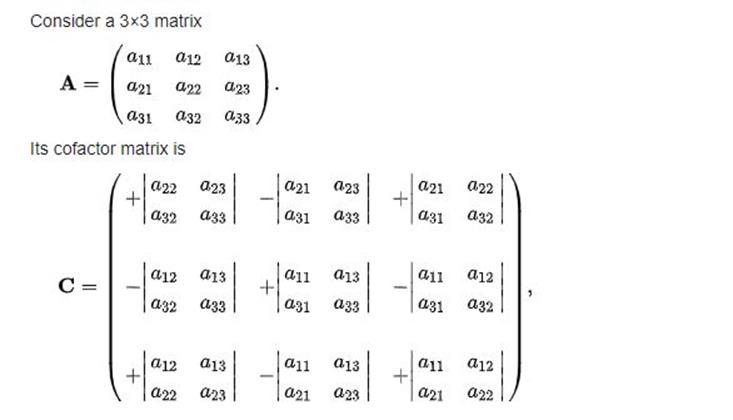
Adjoint of a Matrix:

· The adjoint matrix of A is defined as the transpose of the matrix of cofactors of A. It is denoted by

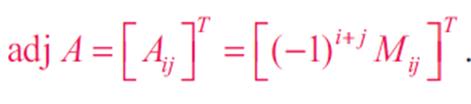
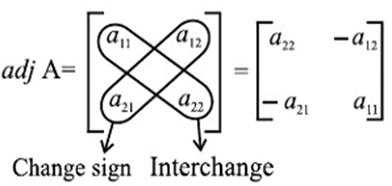
· Adjoint of matrix 2x2

· Example,

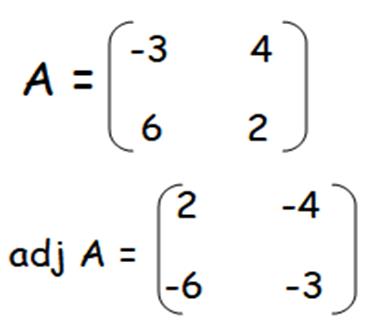
· Adjoint of matrix 3x3

· OR adjoint can also be represented in terms of cofactors and minors,

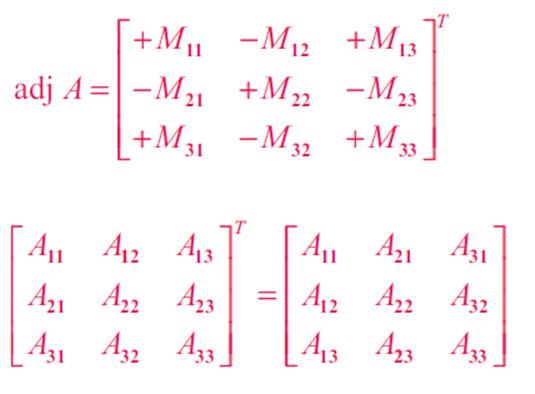
· Examples,

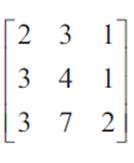
· Consider a Matrix A of order 3x3

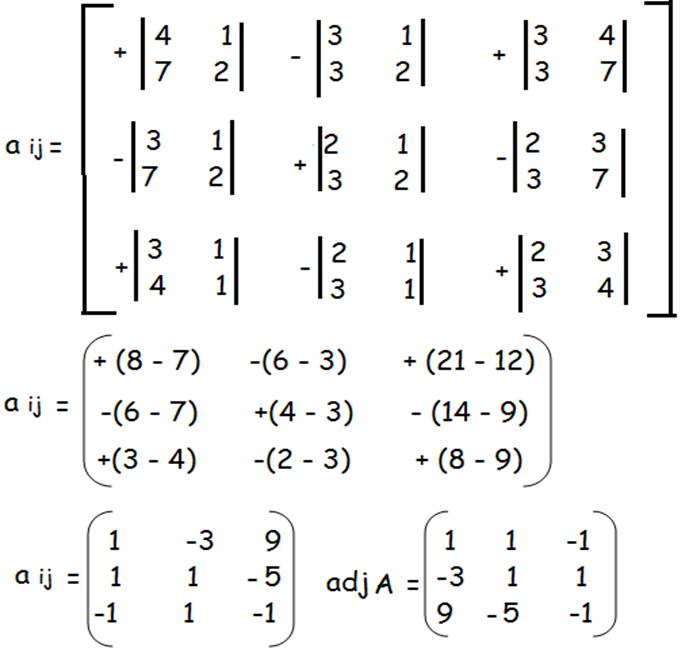
Singular and non-singular Matrix:

· If the value of determinant corresponding to a square matrix is zero, then the matrix is said to be a singular matrix, i.e. if |A| = 0, then it is said to be a singular matrix.

· Otherwise it is non-singular matrix, i.e. for a square matrix A, if |A| ≠ 0, then it is said to be a non-singular matrix.

Inverse of a Matrix:

· The inverse of a matrix can be obtained by the formula given below.

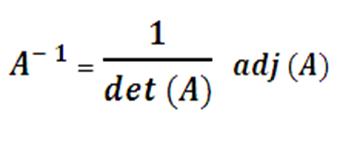
· Provided that the given matrix is a non-singular matrix, i.e. |A| ≠ 0

· Example,

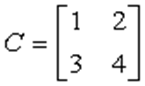
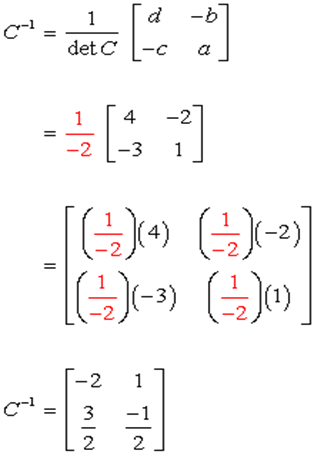
Theorems on Adjoint and Inverse of a Matrix:

Theorem 1

· If A be any given square matrix of order n, then A adj(A) = adj(A) A = |A|I, where I is the identitiy matrix of order n.

Theorem 2

· If A and B are non-singular matrices of the same order, then AB and BA are also non-singular matrices of the same order.

Theorem 3

· The determinant of the product matrices is equal to the product of their respective determinants, that is, |AB| = |A||B|, where A and B are square matrices of the same order.

Theorem 4

· A square matrix A is invertible if and only if A is a non-singular matrix.

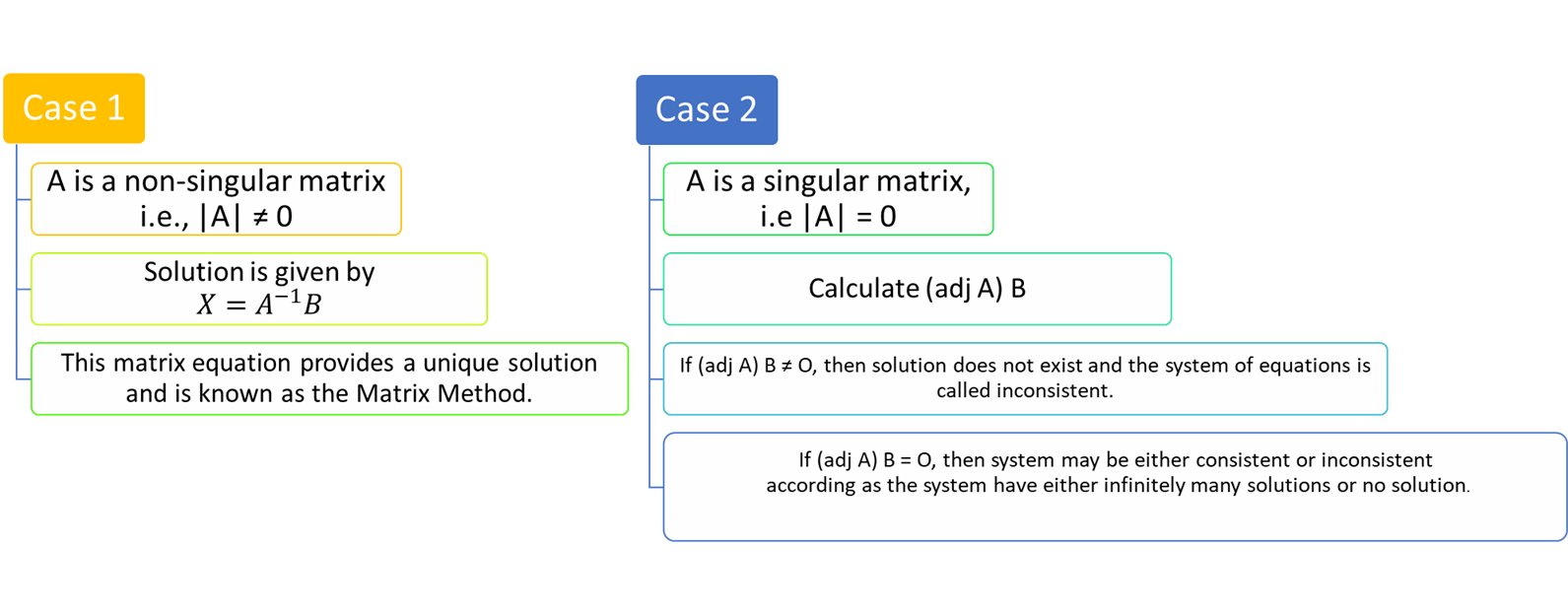
Solution of System of Linear Equations using Inverse of a Matrix:

· A solution for a system of linear Equations can be found by using the inverse of a matrix. Suppose we have the following system of equations

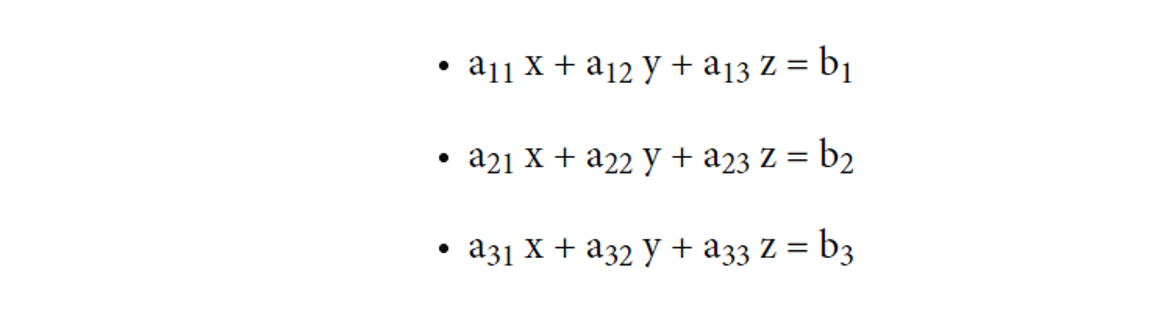
· The above system of equations can be represented in the form of a square matrix as

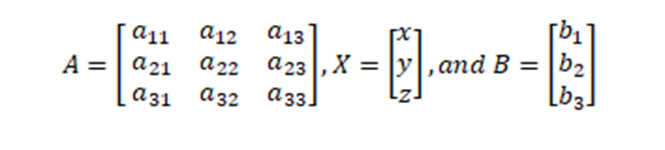
· Here arise two cases