Continuity and Differentiability

Continuity:

· A function is continuous when its graph is a single unbroken curve that you could draw without lifting your pen from the paper.

· Example of a continuous function,

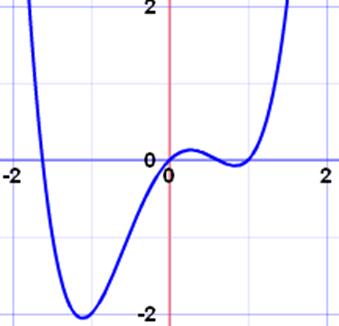
· A formal definition of continuity will be,

· Here existence of limit means,

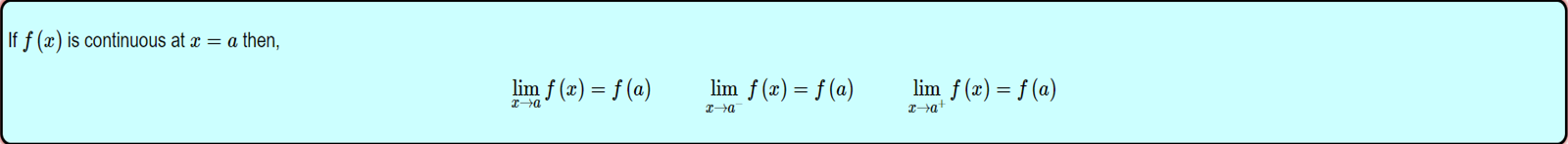
Continuity in a Closed Interval

· A function is said to be continuous on the interval [a,b] if it is continuous at each point in the interval.

· Example,

Discontinuity:

· So what is not continuous also called discontinuous. Several types of discontinuity can happen.

· Holes (Not Continuous)

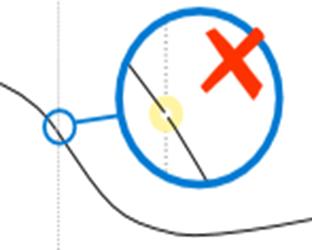
· Jumps (Not Continuous)

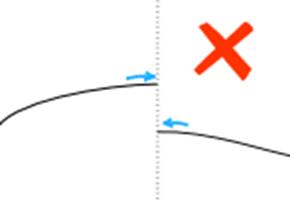
· Vertical Asymptotes (Not Continuous) where the function heads up/down towards infinity.

Algebra of continuous functions:

· Suppose f(x) and g(x) are two continuous functions at the point x = a. Then we have

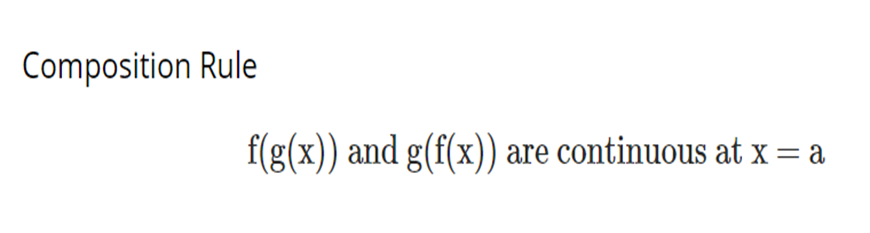
· Example,

Differentiability:

· A derivative is a function that tells us about rates of change, or slopes of tangent lines.

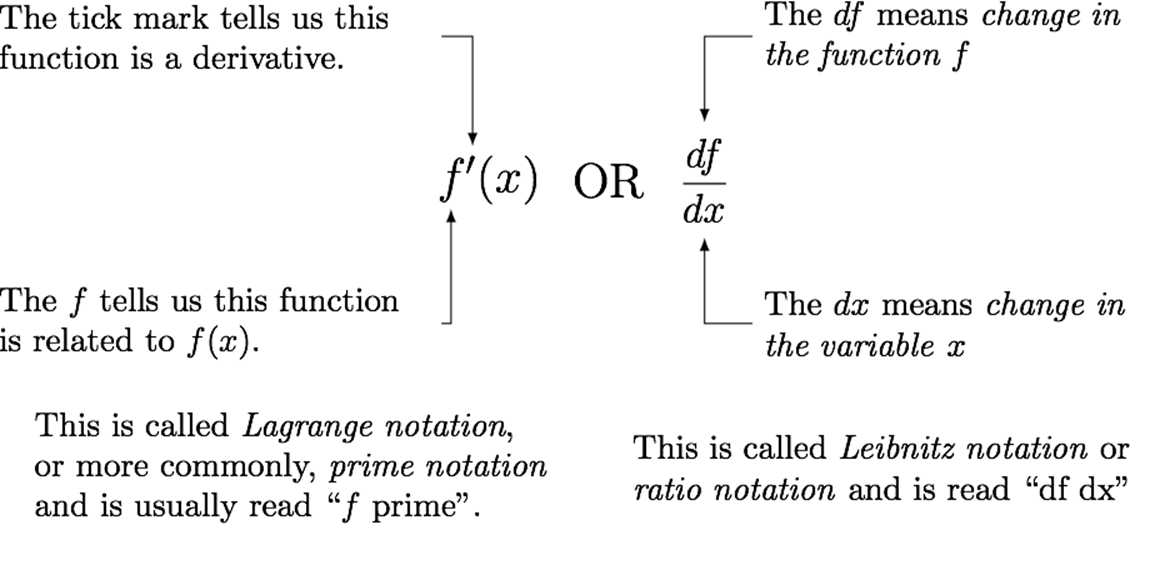
· The differentiability of f(x) with respect to x is the function f′(x) and is defined as,

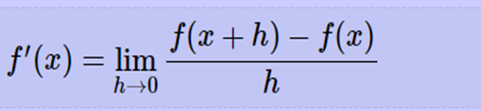
· This definition is also known as First Principle.

· There are two popular variations of the above definition. They are mathematically equivalent to the one given above.

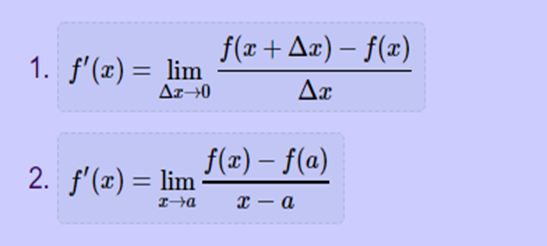
· Example, find derivative using First Principle,

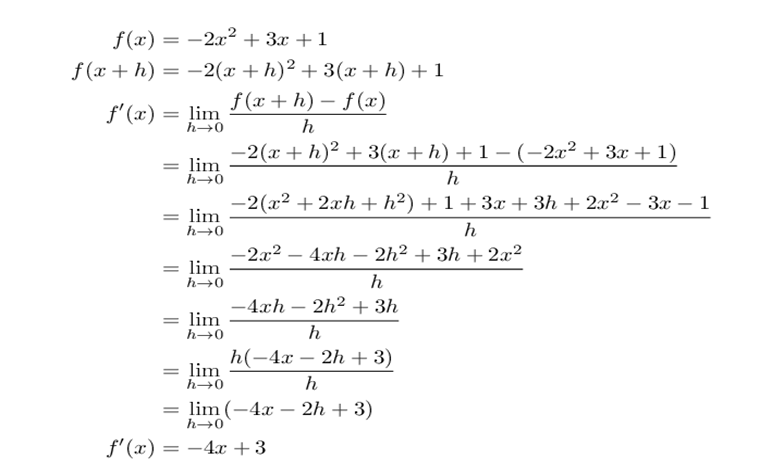
Derivative Formula of Standard Functions:

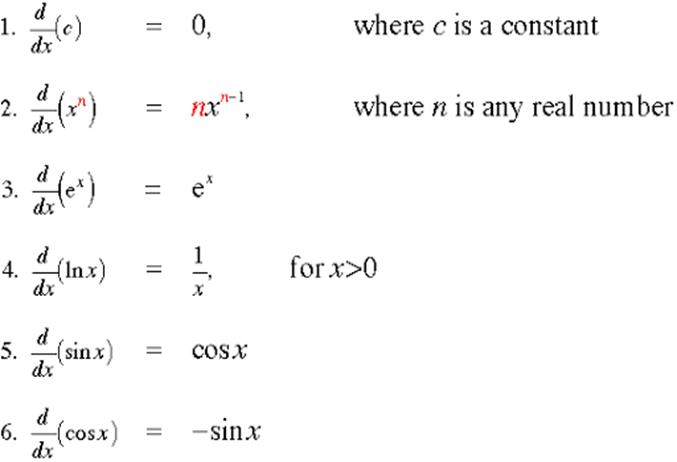
· Suppose f(x) and g(x) are differentiable functions Then...

Derivative of a Sum and Difference:

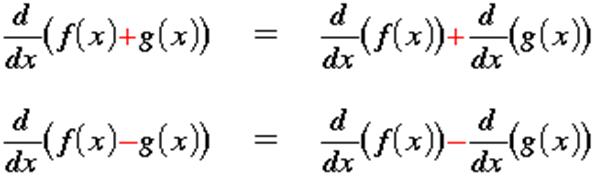
· Example,

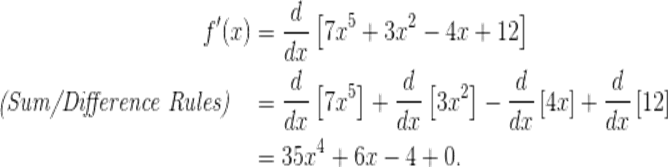
Product/Leibnitz Rule for Derivatives:

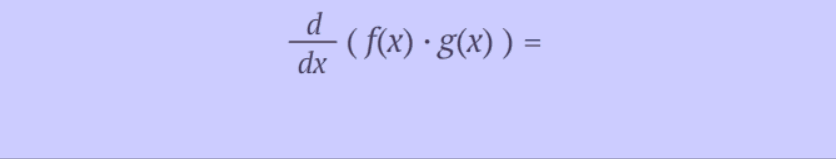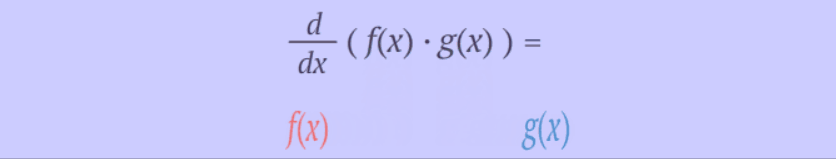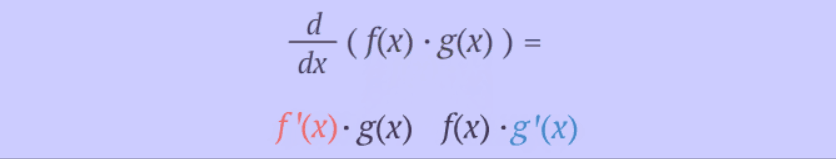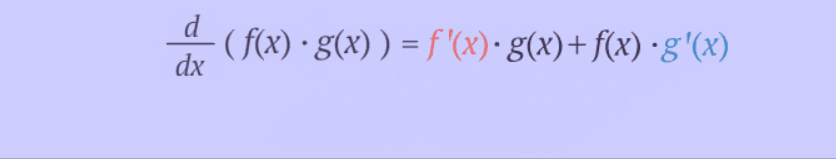
· Example

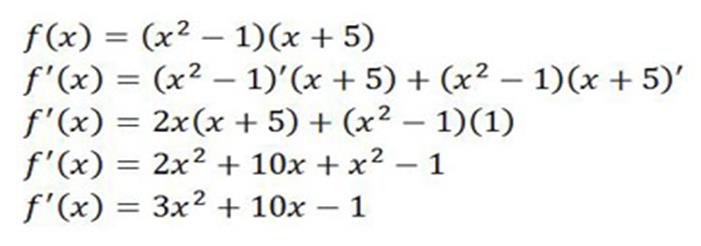
Quotient Rule for Derivatives ():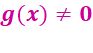

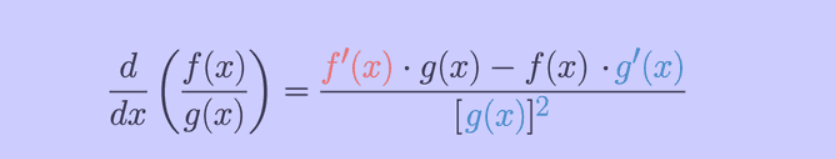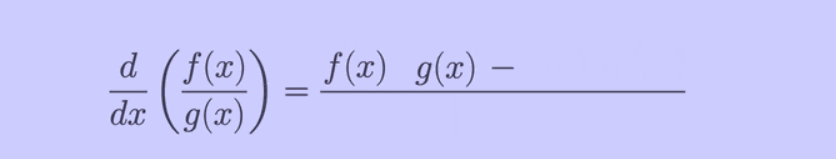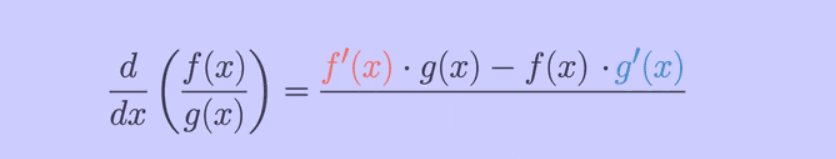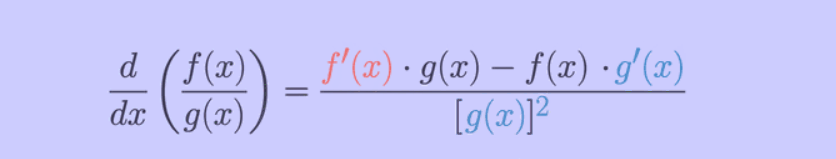
· Examples,

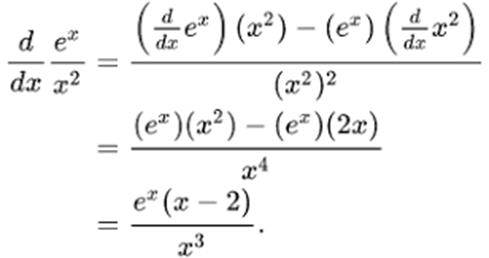
· Examples, power rule,

Derivatives of Composite Functions:

· To solve composite function we will use chain rule, So what is chain rule let’s find out…

Chain Rule

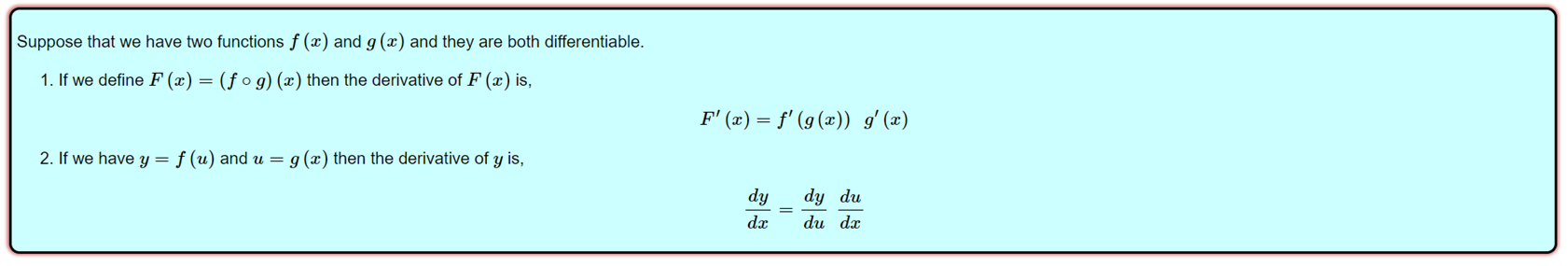
· Suppose 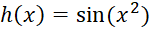. Find h′(x).

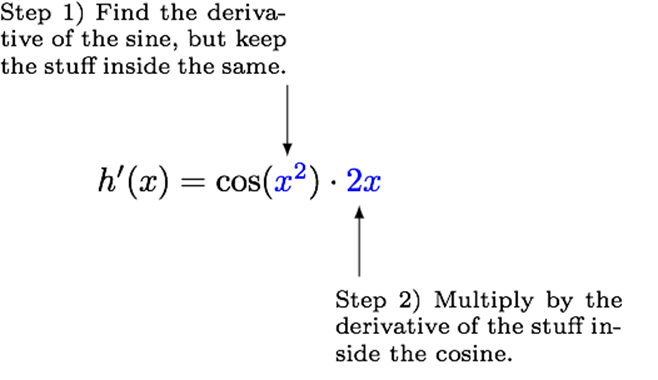
· More Examples on chain rule,

· Find the derivative of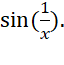

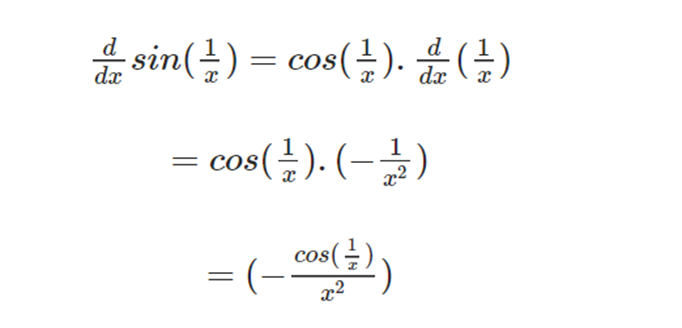
Derivatives of Implicit Functions:

· Explicit Functions: When a function is written so that the dependent variable is isolated on one side of the equation, we call it an explicit function.

· Implicit Functions: When the dependent variable is not isolated, we refer to the equation as being implicitly defined and the y-variable as an implicit function.

· Implicit differentiation relies on the chain rule.

· Examples

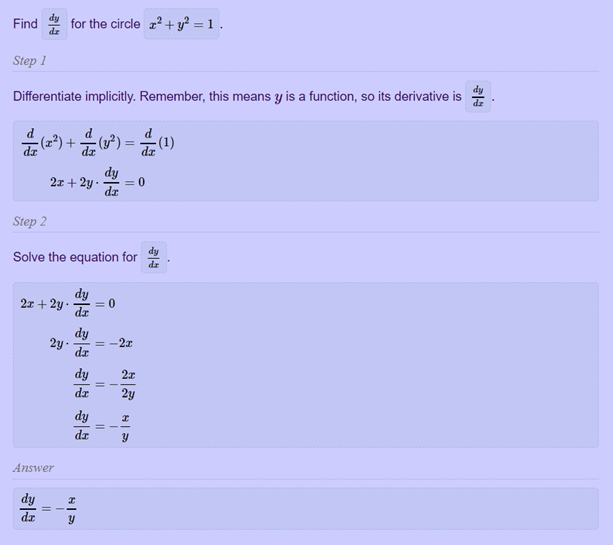
Derivative of Inverse Trigonometric Functions:

· Formulas

· Proof of formula of inverse trigonometric functions,

· Examples,

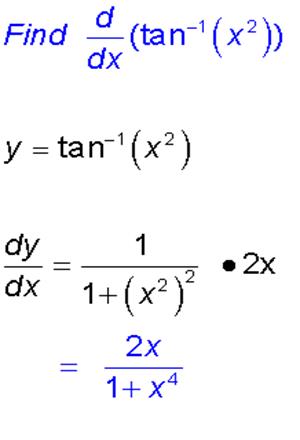
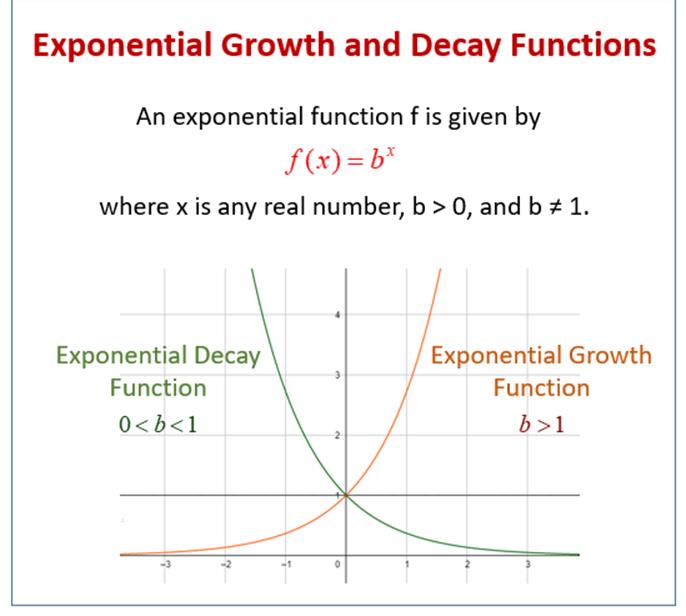
Exponential and Logarithmic Functions:

Exponential Functions:

· Case 1: If b > 1: The exponential function increases very rapidly with increasing x and tends to +∞ as x tends to +∞.

· Case 2: If b < 1: The function decreases very rapidly with increasing x and tends to 0 as x tends to +∞.

· Properties of Exponential Functions:

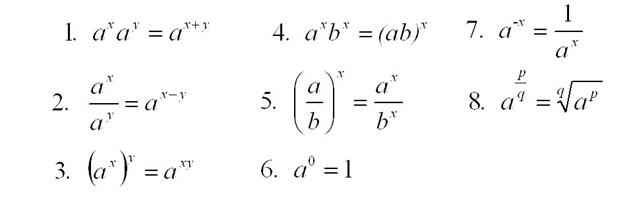
· Derivative Formula of Exponential Functions:

· Examples,

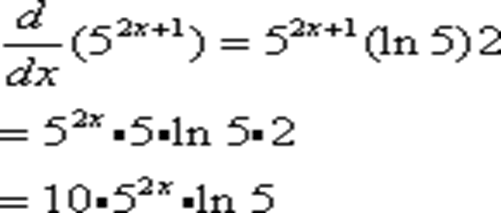
· Logarithmic Functions:

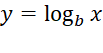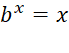· In this definition  is called the logarithm form and  is called the exponential form.

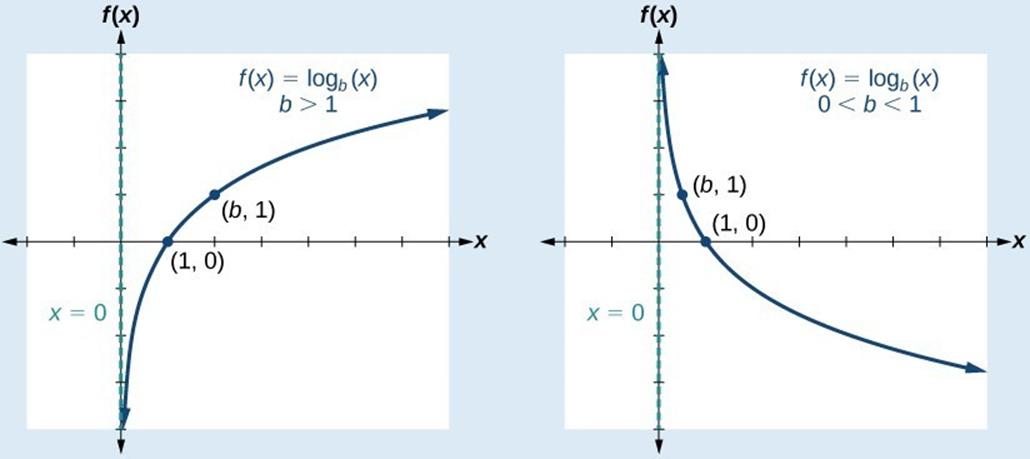
· Case 1: b > 1: Here, the logarithmic function decreases very rapidly with decreasing x and tends to -∞ as x tends to 0.

· Case 2: 0 < b < 1: Here the function increases very rapidly to +∞ as x tends to 0, and falls at an ever decreasing rate to -∞ as x tends to +∞.

· Properties of Logarithmic Functions:

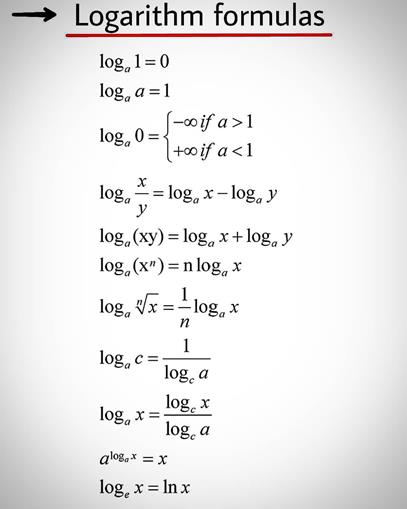
· Derivative Formula of Logarithmic Functions:

· Logarithmic Differentiation

Derivatives of Functions in Parametric Forms:

· If x = f(t) and y = g(t) are two differentiable functions of the parameter t, such that y is defined as a function of x, then :

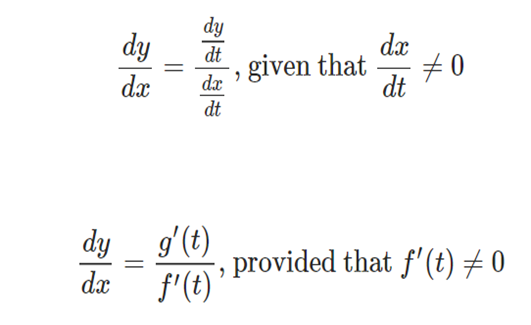
· Example,

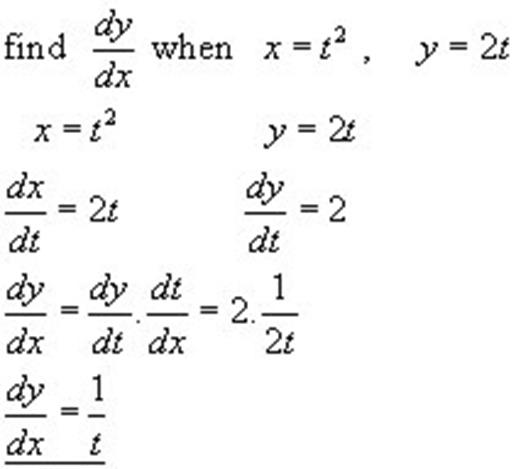
Second Order Derivatives:

· Differentiating a function gives the first derivative.

· Differentiating the first derivative gives the second derivative.

Mean Value Theorem:

Rolle's Theorem

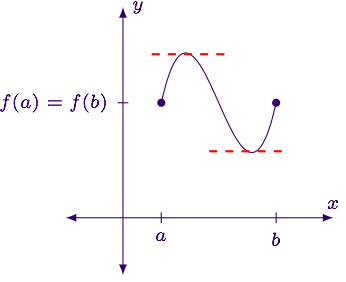
· Suppose f(x) is continuous on [a,b], differentiable on (a,b) and f(a)=f(b). Then there exists some point c∈[a,b] such that f′(c)=0.

· If a function is continuous and differentiable on an interval, and it has the same y-value at the endpoints, then the derivative will be equal to zero somewhere in the interval.

· Graphically, this means there will be a horizontal tangent line somewhere in the interval

· Rolle's Theorem is a special case of the Mean Value Theorem.

Mean Value Theorem

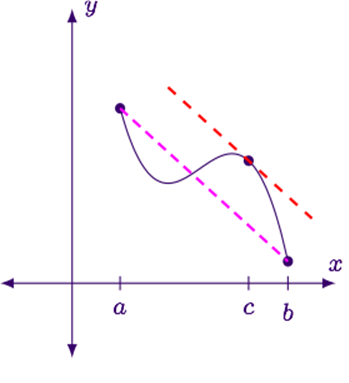
· Suppose f(x) is continuous on [a,b] and differentiable on (a,b). Then there is a point at c ∈ (a, b) where

· The theorem claims the existence of a point in the chosen interval, where the slope of the tangent is the same as the slope of the straight line joining the end-points of that interval.

Summary: