APPLICATION OF INTEGRALS

INTRODUCTION:

An integral is a function, of which a given function is the derivative. Integration is basically used to find the areas of the two-dimensional region and computing volumes of three-dimensional objects. Therefore, finding the integral of a function with respect to x means finding the area to the X-axis from the curve. The integral is also called as anti-derivative as it is the reverse process of differentiation.

Area Under Simple Curves:

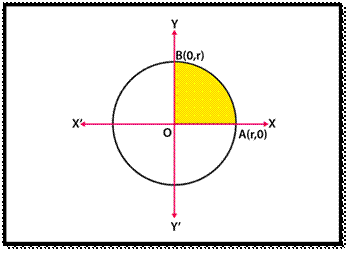
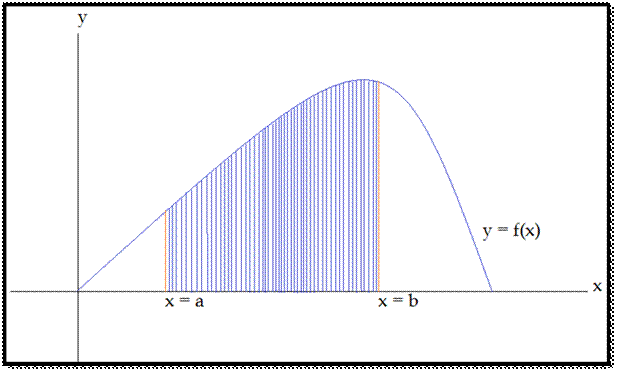
The area A under the curve f(x) bounded by x = a and x = b is given by:

A=∫baf(x)dx

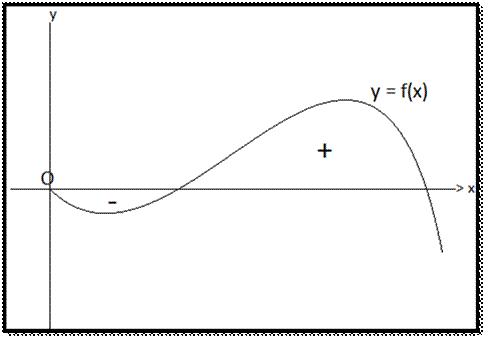
If the area between two bounding values of x on the graph, lies above the x-axis; its sign is taken to be positive.

If the area between two bounding values of x on the graph, lies below the x-axis; its sign is taken to be negative.

Calculation Method

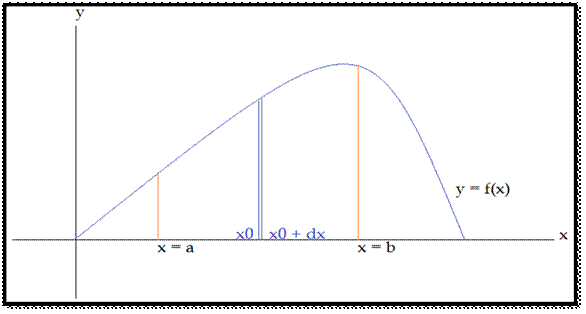
Step 1:

 Form a rectangular strip of height/length = f(x₀) and breadth = dx as shown in the figure below.

You can consider the rectangle to be centered at the value x = x₀

dx is an infinitesimally small value which could be taken equal to the difference in the x-coordinates on which the sides of the rectangle are placed.

Step 2:

Move the strip under the curve, beginning from the lower bound of x i.e. x = a; and terminating at the upper bound of x i.e. x = b, changing the value of x₀ at each point but retaining the same value of dx throughout. Place all of these strips adjacent to each other and get a resultant figure such as:

Step 3:

The area dA of a single rectangular strip = length × breadth

dA=f(x0)×dx

This is known as the Differential/Elementary Area.

Step 4:

The total area A under the curve can be approximately obtained by summing over the areas of all the rectangular strips.

A=∑x0=ax0=bdA

Using the value of dA from a previous step:

A=∑x0=ax0=bf(x0)dx

Step 5:

If dx → 0, the summation can be converted to an integral. Then we have;

A=∫baf(x)dx

The area of the region bounded by a curve and a line

Given a curve C: y = f(x) and a straight line T: y = mx + c. The first step is to plot the area under the curve and the straight line on the same graph.

BOUNDED REGIONS

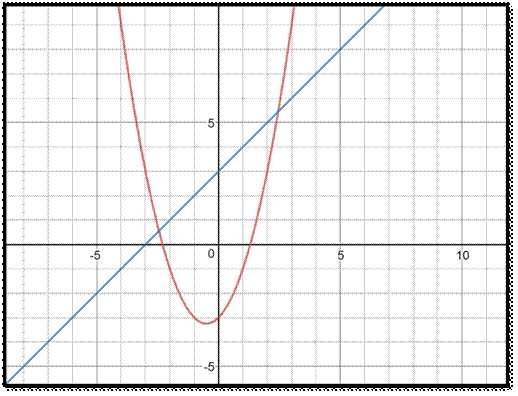
The straight line intersects the curve at two points and forms a bounded region.

The straight line intersects the curve at three points and forms more than 1 bounded region. The total area has a finite value.

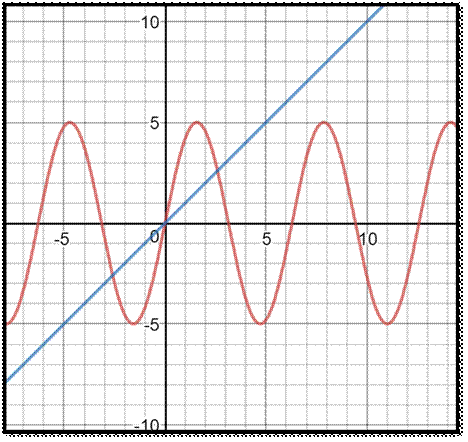
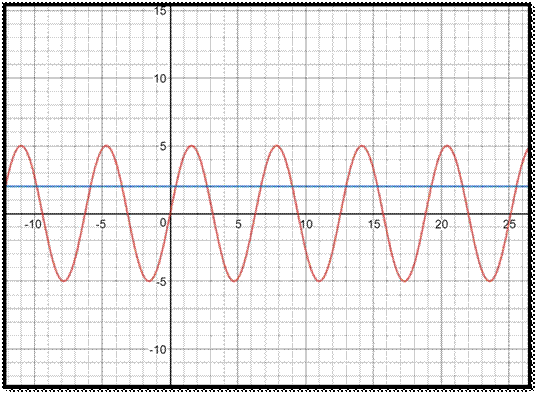
The straight line intersects the curve at an infinite number of points and forms an infinite number of bounded regions. The total area is not finite here.

Calculation of Area Under the Curve Bounded by a Line:

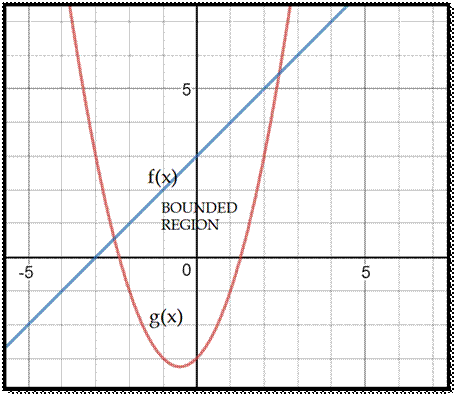
Clearly, we need to calculate the area of the mentioned region in the graph. This region can be viewed as the region common to the ‘Area under the curve’ for both, the straight line as well as the given curve. This simplifies our calculation tremendously. For example, here the straight line T has more area under it than the curve C.

So, the area common to both of them can be found out by subtracting the area under the straight line T from the area under the curve C. The bounding values of x for the calculation of the area under the curves can be found by solving the simultaneous equations for the coordinates of the points of intersection between the straight line and the curve.

Let those points have x-coordinates x₁ and x₂. The area under the curves (say y = f(x)) can be calculated using the formula:

A=∫x2x1f(x)dx

Let the area under the given curve C turn out to be A_C and let the area under the given straight line T turn out to be A_T. Then the area common to both the curves, in this case, will be A = A_T – A_C. A general formula for writing down the area for this case could be given as: 

A=∫x2x1[f(x)–g(x)]dx

where f(x): equation of the straight line and g(x): equation of the curve. Similarly, other cases of the intersection of a straight line and a curve can be analyzed and a general formula could be developed for them.

THEORY:
The equation of the ellipse shown above may be written in the form

Proof:

x ² / a ² + y ² / b ² = 1

Since the ellipse is symmetric with respect to the x and y axes, we can find the area of one quarter and multiply by 4 in order to obtain the total area.
Solve the above equation for y
y = ~+mn~ b √ [ 1 - x ² / a ² ]
The upper part of the ellipse (y positive) is given by
y = b √ [ 1 - x ² / a ² ]
We now use integrals to find the area of the upper right quarter of the ellipse as follows
(1 / 4)

Area of ellipse = ₀^a b √ [ 1 - x ² / a ² ] dx
We now make the substitution sin t = x / a so that dx = a cos t dt and the area is given by
(1 / 4)

Area of ellipse = ₀^π/2 a b ( √ [ 1 - sin² t ] ) cos t dt
√ [ 1 - sin² t ] = cos t since t varies from 0 to π/2, hence
(1 / 4)

Area of ellipse = ₀^π/2 a b cos² t dt
Use the trigonometric identity cos² t = ( cos 2t + 1 ) / 2 to linearize the integrand;
(1 / 4)

Area of ellipse = ₀^π/2 a b ( cos 2t + 1 ) / 2 dt
Evaluate the integral
(1 / 4)

Area of ellipse = (1/2) b a [ (1/2) sin 2t + t ]₀^π/2
= (1/4) π a b
Obtain the total area of the ellipse by multiplying by 4
Area of ellipse = 4 * (1/4) π a b = π a b

Area between Two Curves:

If we have two given curves:

P: y = f(x)

Q: y = g(x)

The first and the most important step is to plot the two curves on the same graph. If one can’t plot the exact curve, at least an idea of the relative orientations of the curves

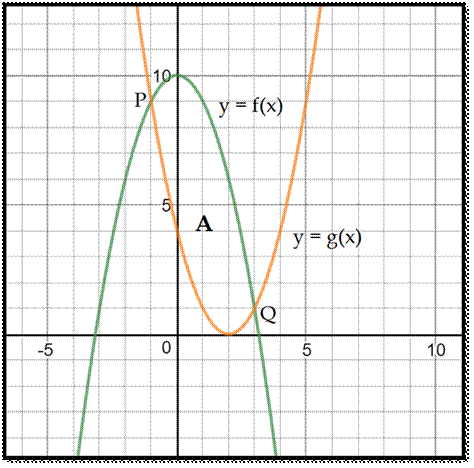
the bounding values of x, in this case, be x₁ and x₂. Then the formula for the area A of the region bounded between the two curves is:

A=∫x2x1[f(x)–g(x)]dx

-à Similarly, if the form of the equations of the curves is such that we have:

P: x = f(y)

Q: x = g(y)

The formula for the area A of the region bounded between the two curves within the domain y = y₁ and y₂, then reduces to the form: 

A=∫y2y1[f(y)–g(y)]dy

Question 1:

Calculate the total area of the region bounded between the curves y = 6x – x²  and y = x².

Answer:

The intersection points of the curve can be solved by putting the value of y = x² into the other equation. We then get:

x² = 6x – x²
2x² -6x = 0
2x(x – 3) = 0
x = 0 / x = 3

Correspondingly we can get the values of y as 0/9. Thus the intersection points can be given as P(3,9) and Q(0,0). The system is as shown below-

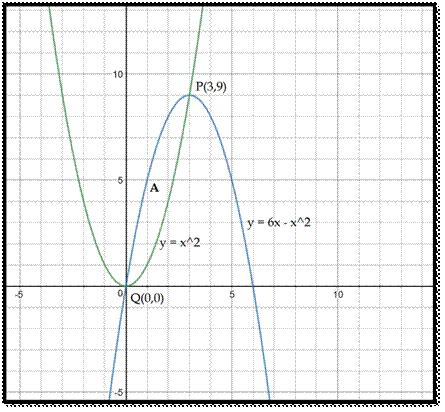
From the graph, the upper curve will be f(x) and the lower one will be g(x). So we have f(x) = 6x – x² and g(x) = x². Then the area:

A=∫x2x1[f(x)–g(x)]dx

A=∫30[6x–x2–x2]dx

A=∫30[6x–2x2]dx

A=[6×x22–2×x33]30

A=(6×92+2×273)–(6×02+2×03)

A=(27+18)–(0+0)

A=45

Since the area is above the y-axis, we will take it with a positive sign. Thus the answer is A = 45.