Differential Equations

Differential Equation:

An equation involving independent variable, dependent variable, derivatives of dependent variable with respect to independent variable and constant is called a differential equation.
e.g.
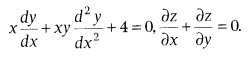
Differential Equations Class 12 Notes Maths Chapter 9 1

Ordinary Differential Equation:

An equation involving derivatives of the dependent variable with respect to only one independent variable is called an ordinary differential equation.
e.g.
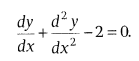
Differential Equations Class 12 Notes Maths Chapter 9 2

From any given relationship between the dependent and independent variables, a differential equation can be formed by differentiating it with respect to the independent variable and eliminating arbitrary constants involved.

Order of a Differential Equation:

Order of a differential equation is defined as the order of the highest order derivative of the dependent variable with respect to the independent variable involved in the given differential equation.
Note: Order of the differential equation, cannot be more than the number of arbitrary constants in the equation.

Degree of a Differential Equation:

The highest exponent of the highest order derivative is called the degree of a differential equation provided exponent of each derivative and the unknown variable appearing in the differential equation is a non-negative integer.
Note
(i) Order and degree (if defined) of a differential equation are always positive integers.
(ii) The differential equation is a polynomial equation in derivatives.
(iii) If the given differential equation is not a polynomial equation in its derivatives, then its degree is not defined.

Formation of a Differential Equation:

To form a differential equation from a given relation, we use the following steps:
Step I: Write the given equation and see the number of arbitrary constants it has.
Step II: Differentiate the given equation with respect to the dependent variable n times, where n is the number of arbitrary constants in the given equation.
Step III: Eliminate all arbitrary constants from the equations formed after differentiating in step (II) and the given equation.
Step IV: The equation obtained without the arbitrary constants is the required differential equation.

Solution of the Differential Equation

A function of the form y = Φ(x) + C, which satisfies given differential equation, is called the solution of the differential equation.
General solution:

The solution which contains as many arbitrary constants as the order of the differential equation, is called the general solution of the differential equation, i.e. if the solution of a differential equation of order n contains n arbitrary constants, then it is the general solution.

Particular solution:

A solution obtained by giving particular values to arbitrary constants in the general solution of a differential equation, is called the particular solution.

Methods of Solving First Order and First Degree Differential Equation
Variable separable form:

Suppose a differential equation is $\frac { dy }{ dx }$ = F(x, y). Here, we separate the variables and then integrate both sides to get the general solution, i.e. above equation may be written as $\frac { dy }{ dx }$ = h(x) . k(y)
Then, by separating the variables, we get $\frac { dy }{ k(y) }$ = h(x) dx.
Now, integrate above equation and get the general solution as K(y) = H(x) + C
Here, K(y) and H(x) are the anti-derivatives of $\frac { 1 }{ K(y) }$ and h(x), respectively and C is the arbitrary constant.

Homogeneous differential equation:

A differential equation $\frac { dy }{ dx } =\frac { f(x,y) }{ g(x,y) }$ is said to be homogeneous, if f(x, y) and g(x, y) are homogeneous functions of same degree, i.e. it may be written as
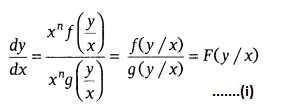
Differential Equations Class 12 Notes Maths Chapter 9 3
To check that given differential equation is homogeneous or not, we write differential equation as $\frac { dy }{ dx }$ = F(x, y) or $\frac { dx }{ dy }$ = F(x, y) and replace x by λx, y by λy to write F(x, y) = λ F(x, y).
Here, if power of λ is zero, then differential equation is homogeneous, otherwise not.

Solution of homogeneous differential equation:

To solve homogeneous differential equation, we put
y = vx
⇒ $\frac { dy }{ dx }$ = v + x $\frac { dv }{ dx }$
in Eq. (i) to reduce it into variable separable form. Then, solve it and lastly put v = $\frac { y }{ x }$ to get required solution.

Note: If the homogeneous differential equation is in the form of $\frac { dy }{ dx }$ = F(x, y), where F(x, y) is homogeneous function of degree zero, then we make substitution $\frac { x }{ y }$ = v, i.e. x = vy and we proceed further to find the general solution as mentioned above.

Linear differential equation:

General form of linear differential equation is
$\frac { dy }{ dx }$ + Py = Q …(i)
where, P and Q are functions of x or constants.
or $\frac { dx }{ dy }$ + P’x = Q’ …(ii)
where, P’ and Q’ are functions of y or constants.
Then, solution of Eq. (i) is given by the equation
y × IF = ∫(Q × IF) dx + C
where, IF = Integrating factor and IF = e^∫Pdx
Also, solution of Eq. (ii) is given by the equation
x × IF = ∫ (Q’ × IF) dy + C
where, IF = Integrating factor and IF = e^∫P’dy