Mensuration

Mensuration is a branch of study that deals with the measurement of length, area, and volume. We think of their regions and boundaries, for this we need to measure them to compare.

Perimeter:

The continuous line forming the boundary of continuous figure.

If you start from a point and move along the line segments then you again reached to the point from where you started. Since you made a compete round of the figure and then that distance covered is equal to the length of wire used to draw the figure.

This distance covered is known as the perimeter of closed figure.

The idea of perimeter is widely used in our daily life.

(i) A farmer who wants to fence his field.

(ii) An engineer who plans to build a compound wall on all sides of a house.

(iii)A person preparing a track to conduct sports.

All these people use the idea of ‘perimeter’.

Perimeter is the distance covered along the boundary forming a closed figure when you go round the figure once.

Example:

Find the perimeter of the following figures:

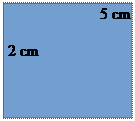(a)

Perimeter = 5+2+5+2 = 14 cm.

So, Simply find the sum of the lengths of all the sides (which are line segments).

Perimeter of rectangle:

Let us consider a rectangle whose length is 15 cm and breadth is 9 cm

Then the perimeter of rectangle is perimeter of the rectangle = sum of all the four sides.

= 15+9+15+9 = 48

= l+b+l+b

=2l+2b

=2(l+b).

Perimeter of a rectangle = length + breadth + length + breadth

i.e. Perimeter of a rectangle = 2 × (length + breadth).

Example: An athlete takes 10 rounds of a rectangular park, 50 m long and 25 m wide. Find the total distance covered by him?

Solution:

Length of the rectangular park = 50 m

Breadth of the rectangular park = 25 m

Total distance covered by the athlete in one round will be the perimeter of the park.

Now, perimeter of the rectangular park = 2 × (length + breadth)= 2 × (50 m + 25 m)

= 2 × 75 m = 150 m.

So, the distance covered by the athlete in one round is 150 m.

Therefore, distance covered in 10 rounds = 10 × 150 m = 1500m The total distance covered by the athlete is 1500 m.

Example: Find the cost of fencing a rectangular park of length 250 m and breadth 175 m at the rate of ` 12 per metre.

Solution: Length of the rectangular park = 250 m

Breadth of the rectangular park = 175 m

To calculate the cost of fencing we require perimeter.

Perimeter of the rectangle = 2 × (length + breadth) = 2 × (250 m + 175 m)

= 2 × (425 m) = 850 m Cost of fencing 1m of park = ` 12

Therefore, the total cost of fencing the park = Rs. 12 × 850 = Rs. 10200.

Perimeter of regular shapes :

Consider this example.

Seema wants to put coloured tape all around a square picture (Fig 10.5) of side 1m as shown. What will be the length of the coloured tape he requires?

Since, Seema wants to put the coloured tape all around the square picture, he needs to find the perimeter of the picture frame.

Thus, the length of the tape required = Perimeter of square = 1m + 1 m + 1 m + 1 m = 4 m

Now, we know that all the four sides of a square are equal, therefore, in place of adding it four times, we can multiply the length of one side by 4.

Thus, the length of the tape required = 4 × 1 m = 4 m.

From this example, we see that Perimeter of a square = 4 × length of a side.

Perimeter of an equilateral triangle = 3 × length of a side.

Example: Pinky runs around a square field of side 75 m, Bob runs around a rectangular field with length 160 m and breadth 105 m. Who covers more distance and by how much?

Solution:

Distance covered by Pinky in one round = Perimeter of the square = 4 × length of a side

= 4 × 75 m = 300 m.

Distance covered by Bob in one round = Perimeter of the rectangle = 2 × (length + breadth)

= 2 × (160 m + 105 m) = 2 × 265 m = 530 m.

Difference in the distance covered = 530 m – 300 m = 230 m.

Therefore, Bob covers more distance by 230 m.

Example:

Find the perimeter of a regular pentagon with each side measuring 3 cm?

Solution: This regular closed figure has 5 sides, each with a length of 3 cm.

Thus, we get Perimeter of the regular pentagon = 5 × 3 cm = 15 cm.

Area:

The amount of surface enclosed by a closed figure is called its area.

In geometry, the area can be defined as the space occupied by a flat shapes or the surface of an object.

The area of a figure is the number of unit squares that cover the surface of a closed figure. Area measures in square units such as square centimetres, square feet, square inches, etc.

Different shapes have different ways to find the area. For Example, in a rectangle we find the area by multiplying the length times the width. In the rectangle, if the area is 2*4 or 8. if you observed or count the small squares you will find there are 8 of them.

Units:

Area is measured in square units.

All the dimension must be in same units.

And is denoted by m². If meter is the unit.

Area of a rectangle:

Area of a rectangle = (length * breadth).

Example: Find the area of a rectangle whose length and breadth are 12 cm and 4 cm respectively?

Solution: Length of the rectangle = 12 cm Breadth of the rectangle = 4 cm

Area of the rectangle = length * breadth = 12 cm * 4 cm = 48 sq cm.

Area of a square:

Area of the square = side * side.

Example: Find the area of a square plot of side 8 m.

Solution: Side of the square = 8 m

Area of the square = side * side = 8 m * 8 m = 64 sq m.

Example: Bob wants to cover the floor of a room 3 m wide and 4 m long by squared tiles. If each square tile is of side 0.5 m, then find the number of tiles required to cover the floor of the room? Solution: Total area of tiles must be equal to the area of the floor of the room.

Length of the room = 4 m Breadth of the room = 3 m

Area of the floor = length * breadth = 4 m * 3 m = 12 sq m

Area of one square tile = side * side = 0.5 m * 0.5 m = 0.25 sq m

Number of tiles required = Area of the floor /Area of one tile = 12/ 0.25

= 1200 25 48tiles.

Example: Find the area in square metre of a piece of cloth 1m 25 cm wide and 2 m long?

Solution: Length of the cloth = 2 m

Breadth of the cloth = 1 m 25 cm = 1 m + 0. 25 m = 1.25 m (since 25 cm = 0.25m)

Area of the cloth = length of the cloth * breadth of the cloth

= 2 m * 1.25 m = 2.50 sq m.

Summary:

1. Perimeter is the distance covered along the boundary forming a closed figure when you go round the figure once.

2. (a) Perimeter of a rectangle = 2 * (length + breadth)

(b) Perimeter of a square = 4 * length of its side

(c) Perimeter of an equilateral triangle = 3 * length of a side

3. Figures in which all sides and angles are equal are called regular closed figures.

4. The amount of surface enclosed by a closed figure is called its area.

5. To calculate the area of a figure using a squared paper, the following conventions are adopted:

(a) Ignore portions of the area that are less than half a square.

(b) If more than half a square is in a region. Count it as one square.

(c) If exactly half the square is counted, take its area as 1/2 sq units.

6. (a) Area of a rectangle = length * breadth

(b) Area of a square = side * side.