Whole Numbers
Counting Numbers or Natural Numbers
The numbers 1, 2, 3, are called natural numbers or counting numbers.
Whole Numbers
Let us add one more number i.e., zero (0), to the collection of natural numbers. Now the numbers are 0, 1, 2,… These numbers are called whole numbers.
We can say that whole numbers consist of zero and the natural numbers. Therefore, except zero all the whole nos. are natural numbers.
Facts of Whole numbers
Ø The smallest natural number is 1.
Ø The number 0 is the first and the smallest whole numbers.
Ø There are infinitely many or uncountable number of whole-numbers.
Ø All natural numbers are whole-numbers.
Ø All whole-numbers are not natural numbers. For example, 0 is a whole-number but it is not a natural number.
The first 50 whole numbers are
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40,
41, 42, 43, 44, 45, 46, 47, 48, 49, 50
Some other Important terms to remember
|
SUCCESSOR |
PREDECESSOR |
|
F The successor of a whole number is the number obtained by adding 1 to it. F Clearly, the successor of 1 is 2; successor of 2 is 3; successor of 3 is 4 and so on. |
F The predecessor of a whole number is one less than the given number. F Clearly, the predecessor of 1 is 0; predecessor of 2 is 1; predecessor of 3 is 2 and so on. F The whole number 0 does not have any predecessor. |
Example
1) Write the successor of
(a) 10701 (b) 100499 (c) 5099999 (d) 5670
Solution:
a) 10702
b) 100500
c) 5100000
d) 5671
2) Write the predecessor of
(a) 14 (b) 100000 (c) 8090 (d) 4321
Solution:
a) 12
b) 99999
c) 8089
d)4320
Number Line
A line on which numbers are marked at equal intervals to show simple numerical operations is called a number line.
In order to represent whole numbers on a number line, we draw a straight line and mark a point O on it.
From ‘0’ point, mark points 1, 2, 3, 4, 5, 6, 7, 8, 9, etc. on the line at equal intervals to the right of ‘0’.

The arrow-head on the right-side on the number line shows that the numbers can continue up to infinity. With the help of number line we can compare two whole numbers (i.e. we can easily find out which number is greater or smaller).
On the number line we see that the number 6 is on the right of 3.
Hence 6 is greater than 3 (i.e. 6 > 3). Number 1 lies on the left of 3.
Therefore 1 is smaller than 3 (i.e. 1 < 3).
Addition on the number line
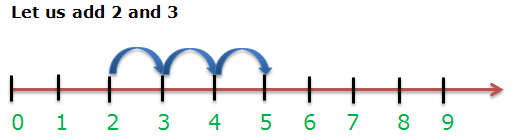
Here, 3 is added to the given number i.e. 2, so we will make 3 jumps to the right of 2.
i.e. 1st jump – from 2 to 3,
2nd jump – 3 to 4
And 3rd jump – 4 to 5
Therefore, the sum of 2 and 3 is 5
Subtraction on the number line
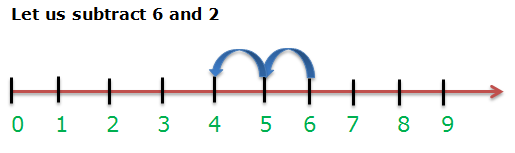
Here, 2 is subtracted from the given number i.e. 6, so we will make 2 jumps to the left of 6.
i.e. 1st jump – from 6 to 5,
And 2nd jump – 5 to 4
Therefore, we get 6 – 2 = 4
Multiplication on the number line
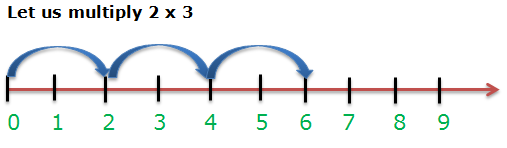
Start from 0, move 2 units at a time to the right, make such 3 moves. And we will reach 6.
So, we say, 2 × 3 = 6.
Properties of Whole Numbers
Closure Property
Closure property on Addition for Whole
Number
0+2=2
1+3=4
5+6=11
So Whole number are closed on Addition
Closure property on Multiplication for
Whole Number
0×2=0
1×4=4
5×1=5
So Whole number are closed on Multiplication
Closure property on subtraction of Whole
number
5−0=5
0−5=?
1−3=?
3−1=2
So Whole number are not closed on Subtraction
Closure property on Division of Whole
number
![]() =2
=2
![]() =?
=?
![]() =0
=0
![]() =?
(Division by Zero is undefined)
=?
(Division by Zero is undefined)
So Whole
Number are not closed on Division
|
Closure Property |
If a and b are any two whole numbers, then a+b, axb are also whole numbers. |
Commutative property
Commutativity property on Addition for
Whole Number
0+2=2+0=2
So Whole number are Commutative on Addition
Commutativity property on Multiplication
for Whole Number
0×2=0 or 2×0=0
So Whole number are Commutative on Multiplication
Commutativity property on subtraction of
Whole number
5−0=5 but 0−5=?
So Whole number are not Commutative on Subtraction
Commutativity property on Division of Whole
number
![]() =2
but
=2
but ![]() =?
=?
So Whole Number are not Commutative on Division
You can add two whole numbers in any order. You can multiply
two whole numbers in
any order.
|
Commutative property |
If a and b are any two whole numbers, then a+b=b+aa+b=b+a and a×b=b×aa×b=b×a |
Associative property
Associativity property on Addition for
Whole Number
0+(2+3)=(0+2)+3=5
1+(2+3)=6=(1+2)+3
So Whole number are Associative on Addition
Associativity property on Multiplication for Whole Number
0×(2×3)=0 or (0×2)×3=0
So Whole number are Associative on Multiplication
Associativity property on subtraction of
Whole number
10−(2−1)=9 but (10−2)−1=7
So Whole number are not Associative on Subtraction
Associativity property on Division of Whole
number
16÷(4÷2)=8 but (16÷4)÷2 =2
So Whole Number are not Associative on Division
If
a, b and c are any two whole numbers, then (a+b)+c = a+(b+c) and (a×b)×c = a×(b×c).
Distributive property
If a, b and c are any two whole numbers, then a(b+c)=a×b+a×c
Additive Identity
If a is any whole number, then a+0=a=0+a.
Example
2+0=2
0+3=3
5+0=5
Multiplicative Identity
If a is any whole number, then a×1=a=1×a.
Example
1×1=1
5×1=5
6×1=6
Multiplication by zero
If a is any whole number, then a×0=0=0×a.
Example
1×0=0
5×0=0
0×0=0
Division by zero
If a is any whole number, then a ÷ 0 is not defined.