Congruence of Triangles

7.1 Introduction

The relation of two objects being congruent is called congruence. For the present, we will deal with plane figures only, although congruence is a general idea applicable to three-dimensional shapes also.

7.2 Congruence of Plane Figures

Look at the two figures given here (Fig 7.3). Are they congruent?

1. You can use the method of superposition. Take a trace-copy of one of them and place.

2. Alternatively, you may cut out one of them and place it over the other. Beware! You are not allowed to bend, twist or stretch the figure that is cut out (or traced out). Ce it over the other. If the figures cover each other completely, they are congruent.

3. In Fig 7.3, if figure F1 is congruent to figure F2, we write F1 ≅ F2.

7.3 Congruence among Line Segments

When are two line segments congruent? Observe the two pairs of line segments given here

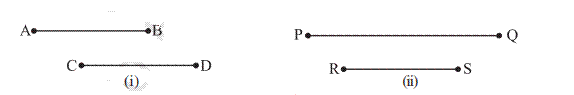
· Use the ‘trace-copy’ superposition method for the pair of line segments in [Fig 7.4(i)]. Copy CD and place it on AB. You find that CD covers AB, with C on A and D on B. Hence, the line segments are congruent. We write AB ≅ CD.

· Repeat this activity for the pair of line segments in

· What do you find? They are not congruent. How do you know it? It is because the line segments do not coincide when placed one over other.

· You should have by now noticed that the pair of line segments in matched with each other because they had same length; and this was not the case in

· In view of the above fact, when two line segments are congruent, we sometimes just say that the line segments are equal; and we also write AB=CD. (What we actually mean is AB≅ CD).

7.4 Congruence of Angles

Look at the four angles given here (

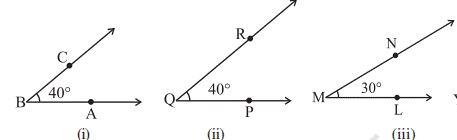
· Make a trace-copy of ∠PQR. Try to superpose it on ∠ABC. For this, first place Q on B and QP along BA . Where does QR fall? It falls on BC .

· Thus, ∠PQR matches exactly with ∠ABC. That is, ∠ABC and ∠PQR are congruent.

· (Note that the measurement of these two congruent angles are same).

We write ∠ABC ≅ ∠PQR…….. (i)

Or m∠ABC = m ∠PQR(In this case, measure is 40°).

· Now, you take a trace-copy of ∠LMN. Try to superpose it on ∠ABC. Place M on B and ML along BA. Does MN fall on BC? No, in this case it does not happen. You find that ∠ABC and ∠LMN do not cover each other exactly. So, they are not congruent.

(Note that, in this case, the measures of ∠ABC and ∠LMN are not equal).

· What about angles ∠XYZ and ∠ABC? The rays YX and YZ , respectively appear to be longer than BA and BC . You may, hence, think that ∠ABC is ‘smaller’ than ∠XYZ. But remember that the rays in the figure only indicate the direction and not any length. On superposition, you will find that these two angles are also congruent.

We write ∠ABC ≅ ∠XYZ….. (ii) Or

m∠ABC = m∠XYZ

In view of (i) and (ii),

We may even write

∠ABC ≅ ∠PQR ≅ ∠XYZ

· If two angles have the same measure, they are congruent. Also, if two angles are congruent, their measures are same

· As in the case of line segments, congruency of angles entirely depends on the equality of their measures. So, to say that two angles are congruent, we sometimes just say that the angles are equal; and we write

∠ABC = ∠PQR (to mean ∠ABC ≅ ∠PQR).

7.5 Congruence of Triangles

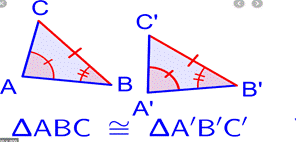
● We saw that two line segments are congruent where one of them, is just a copy of the other. Similarly, two angles are congruent if one of them is a copy of the other. We extend this idea to triangles.

● Two triangles are congruent if they are copies of each other and when superposed, they cover each other exactly.

∆ABC and ∆PQR have the same size and shape. They are congruent. So, we would express this as

∆ABC ≅ ∆PQR

This means that, when you place ∆PQR on ∆ABC, P falls on A, Q falls on B and R falls on C, also PQ falls along AB, QR falls along BC and PR falls along AC. If, under a given correspondence, two triangles are congruent, then their corresponding parts (i.e., angles and sides) that match one another are equal. Thus, in these two congruent triangles, we have:

Corresponding vertices: A and P, B and Q, C and R.

Corresponding sides: AB and PQ, BC and QR, AC and PR.

Corresponding angles: ∠A and ∠P, ∠B and ∠Q, ∠C and ∠R.

If you place ∆PQR on ∆ABC such that P falls on B, then, should the other vertices also correspond suitably? It need not happen! Take trace, copies of the triangles and try to find out.

This shows that while talking about congruence of triangles, not only the measures of angles and lengths of sides matter, but also the matching of vertices. In the above case, the correspondence is

A ↔ P, B ↔ Q, C ↔ R

We may write this as ABC ↔ PQR

Example 1 ∆ABC and ∆PQR are congruent under the correspondence: ABC ↔ RQP Write the parts of ∆ABC that correspond to (i) PQ (ii) ∠Q (iii) RP

Solution

For better understanding of the correspondence, let us use a diagram

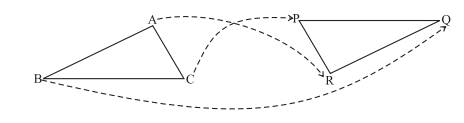
The correspondence is ABC ↔ RQP.

This means A ↔ R; B ↔ Q; and C ↔ P.

So,

(i) PQ ↔ CB

(ii) ∠Q ↔ ∠B

(iii) RP ↔ AC

7.6 Criteria for Congruence Of Triangles

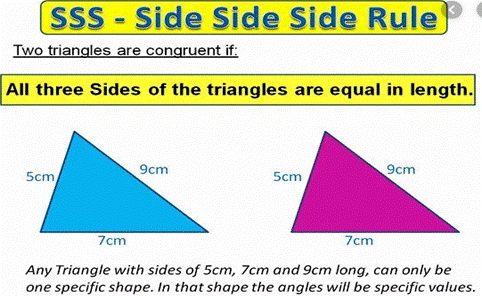
● SSS Congruence criterion:

If under a given correspondence, the three sides of one triangle are equal to the three corresponding sides of another triangle, then the triangles are congruent

Example 2

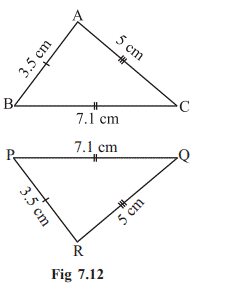
In triangles ABC and PQR, AB = 3.5 cm, BC = 7.1 cm, AC = 5 cm, PQ = 7.1 cm, QR = 5 cm and PR = 3.5 cm. Examine whether the two triangles are congruent or not. If yes, write the congruence relation in symbolic form.

Solution

Here, AB = PR (= 3.5 cm),

BC = PQ (= 7.1 cm) and

AC = QR (= 5 cm)

This shows that the three sides of one triangle are equal to the three sides of the other triangle. So, by SSS congruence rule, the two triangles are congruent.

From the above three equality relations, it can be easily seen that

A ↔ R, B ↔ P and C ↔ Q.

So, we have ∆ABC ≅ ∆RPQ

Important note:

The order of the letters in the names of congruent triangles displays the corresponding relationships. Thus, when you write ∆ABC ≅ ∆RPQ, you would know that A lies on R, B on P, C on Q, AB along RP, BC along PQ and AC along RQ.

Example 3

In Fig 7.13, AD = CD and AB = CB. (i) State the three pairs of equal parts in ∆ABD and ∆CBD. (ii) Is ∆ABD ≅ ∆CBD? Why or why not? (iii) Does BD bisect ∠ABC? Give reasons.

Solution

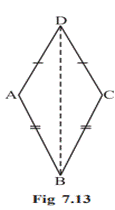
(i) In ∆ABD and ∆CBD, the three pairs of equal parts are as given below:

AB = CB (Given) AD = CD (Given) and

BD = BD (Common in both)

(ii) From (i) above, ∆ABD ≅ ∆CBD (By SSS congruence rule)

(iii) ∠ABD = ∠CBD (Corresponding parts of congruent triangles) So, BD bisects ∠ABC.

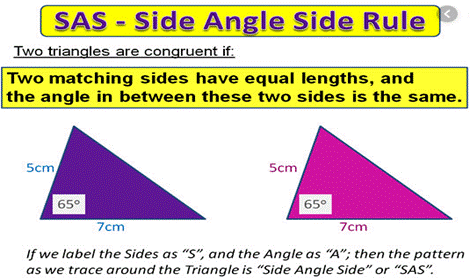
SAS Congruence criterion:

If under a correspondence, two sides and the angle included between them of a triangle are equal to two corresponding sides and the angle included between them of another triangle, then the triangles are congruent

Example 4

Given below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, by using SAS congruence rule. If the triangles are congruent, write them in symbolic form.

∆ABC

(a) AB = 7 cm, BC = 5 cm, ∠B = 50°

(b) AB = 4.5 cm, AC = 4 cm, ∠A = 60°

(c) BC = 6 cm, AC = 4 cm, ∠B = 35°

∆DEF

(a)DE = 5 cm, EF = 7 cm, ∠E = 50°

(b)DE = 4 cm, FD = 4.5 cm, ∠D = 55°

(c)DF = 4 cm, EF = 6 cm, ∠E = 35°

(It will be always helpful to draw a rough figure, mark the measurements and then probe the question).

Solution

(a) Here, AB = EF (= 7 cm), BC = DE (= 5 cm) and included ∠B = included ∠E (= 50°). Also, A ↔ F B ↔ E and C ↔ D.

Therefore, ∆ABC ≅ ∆FED (By SAS congruence rule)

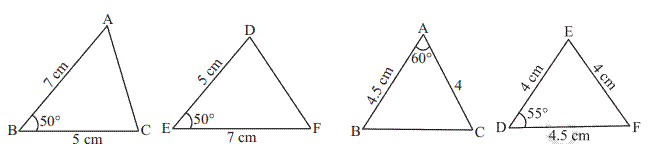
(b) Here, AB = FD and AC = DE. But included ∠A ≠ included ∠D. So, we cannot say that the triangles are congruent.

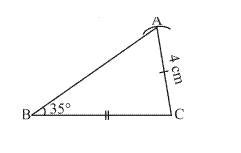
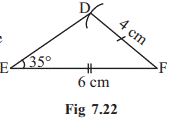
(c) Here, BC = EF, AC = DF and ∠B = ∠E. But ∠B is not the included angle between the sides AC and BC. Similarly, ∠E is not the included angle between the sides EF and DF. So, SAS congruence rule cannot be applied and we cannot conclude that the two triangles are congruent.

Example 5

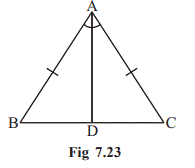
In Fig 7.23, AB = AC and AD is the bisector of ∠BAC. (i) State three pairs of equal parts in triangles ADB and ADC.

(ii) Is ∆ADB ≅ ∆ADC? Give reasons. (iii) Is ∠B = ∠C? Give reasons.

Solution

(i) The three pairs of equal parts are as follows:

AB = AC (Given) ∠BAD = ∠CAD (AD bisects ∠BAC) and AD = AD (common)

(ii) Yes, ∆ADB ≅ ∆ADC (By SAS congruence rule)

(iii) ∠B = ∠C (Corresponding parts of congruent triangles)

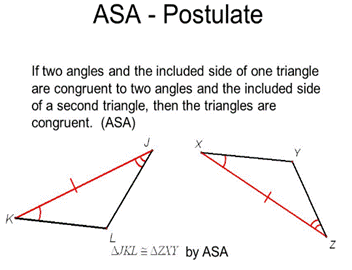
ASA Congruence criterion:

If under a correspondence, two angles and the included side of a triangle are equal to two corresponding angles and the included side of another triangle, then the triangles are congruent.

Example 6

By applying ASA congruence rule, it is to be established that ∆ABC ≅∆QRP and it is given that BC = RP. What additional information is needed to establish the congruence?

Solution

For ASA congruence rule, we need the two angles between which the two sides BC and RP are included. So, the additional information is as follows: ∠B = ∠R and ∠C = ∠P

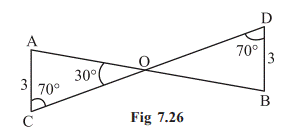
Example 7 In Fig 7.26, can you use ASA congruence rule and conclude that ∆AOC ≅ ∆BOD?

Solution

In the two triangles AOC and BOD, ∠C = ∠D (each 70°)

Also, ∠AOC = ∠BOD = 30° (vertically opposite angles)

So, ∠A of ∆AOC = 180° – (70° + 30°) = 80° (using angle sum property of a triangle) similarly, ∠B of ∆BOD = 180° – (70° + 30°) = 80°

Thus, we have ∠A = ∠B, AC = BD and ∠C = ∠D

Now, side AC is between ∠A and ∠C and side BD is between ∠B and ∠D.

So, by ASA congruence rule,

∆AOC ≅ ∆BOD

7.7 Congruence Among Right-Angled Triangles

RHS Congruence criterion:

If under a correspondence, the hypotenuse and one side of a right-angled triangle are respectively equal to the hypotenuse and one side of another right-angled triangle, then the triangles are congruent.

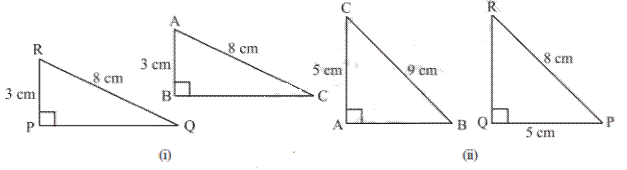
Example 8

Given below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, using RHS congruence rule. In case of congruent triangles, write the result in symbolic form:

∆ABC

1. ∠B = 90°, AC = 8 cm, AB = 3 cm

2. ∠A = 90°, AC = 5 cm, BC = 9 cm

∆PQR

1. ∠P = 90°, PR = 3 cm, QR = 8 cm

2. ∠Q = 90°, PR = 8 cm, PQ = 5 cm

Solution

(i) Here, ∠B = ∠P = 90º,

Hypotenuse, AC = hypotenuse, RQ (= 8 cm) and side AB = side RP (= 3 cm)

So, ∆ABC ≅ ∆RPQ (By RHS Congruence rule).

(ii) Here, ∠A = ∠Q (= 90°) and

Side AC = side PQ (= 5 cm).

But hypotenuse BC ≠ hypotenuse PR

So, the triangles are not congruent

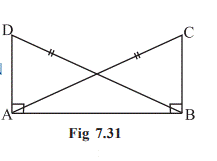
Example 9 In Fig 7.31, DA ⊥ AB, CB ⊥ AB and AC = BD. State the three pairs of equal parts in ∆ABC and ∆DAB. Which of the following statements is meaningful? (i) ∆ABC ≅ ∆BAD (ii) ∆ABC ≅ ∆ABD

Solution

The three pairs of equal parts are:

∠ABC = ∠BAD (= 90°)

AC = BD (Given)

AB = BA (Common side)

From the above,

∆ABC ≅ ∆BAD (By RHS congruence rule).

So, statement

(i) Is true Statement

(ii) is not meaningful, in the sense that the correspondence among the vertices is not satisfied.