Data Handling
Introduction
Ø Data is a collection of numbers gathered to give some information.
Ø It could be the marks of students, shopping done in an year, attendance of students, weight of some individuals and so on.
Ø For eg, the marks of students in the class or the amount of various goods shopped from the market.

Ø The collection, recording and presentation of data help us organize our experiences and draw inferences from them.
Ø Before collecting data it is important to know what we would use it for.
Ø Proper organization of data is very important since it ensures that data is easy to understand and interpret.
Mean
Ø Different forms of data need different forms of representative or central value to represent it.
Ø One of the representative values is arithmetic mean. It is also called as mean.
The average or arithmetic mean is defined as:
Mean
= ![]()
Ø Mean is the most common representative value of a data.
Ø It values between the maximum and minimum observation of a data.
Problem:
The height of Ram is 150 m and the height of Rama is 132m.What is the average height?

Solution:
Height of Ram = 150 m
Height of Rama = 132m
Number of observations = 2
Mean= Sum of observations/Number of observations
Mean = (Height of Ram+ Height of Rama)/2
Mean = (150+132)/2
Mean = 282/2
Mean = 141
So, the average height is 141 m.
Range
Ø Range is another representative value of the data.
Ø Range is defined as the difference between the highest and the lowest observation.
Ø It gives us an idea of the spread of the observations.
Ø This can be found by subtracting the lowest observation from the highest observation.
Range = Highest value – lowest value
This tells us about the spread of data.
Problem:
Consider the following marks of twenty students and answer the questions that follow:
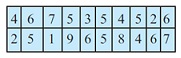
Marks can be arranged in a tabular form first.
Solution:
Which number is the highest?
The table shows the marks obtained by twenty students. The highest marks obtained by a student are 9.
Which number is lowest?
The table shows the marks obtained by twenty students. The lowest marks obtained by a student are 1.
What is the range of data?
Range is the difference between the highest and the lowest observation. The highest marks are 9 and the lowest marks are 1.
Range = 9 - 1
= 8
Find the arithmetic mean.
Arithmetic mean is given as:
= ![]()
Mean = 100/20
= 5
Mode
Ø Mode is another form of central tendency or representative value.
Ø The mode of a set of observations is the observation that occurs most often.
Ø When the number of observations is large, observing them together is not easy.
Ø In case of large data, tabulation can be done by putting tally marks and finding the frequency.
Ø The observation with the highest frequency is the mode of the data.
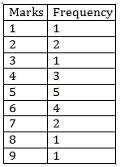
Problem
The scores in mathematics test (out of 25) of 15 students is as follows:
19, 25, 23, 20, 9, 20, 15, 10, 5, 16, 25, 20, 24, 12, 20
Find the mode of this data.
Solution:
Firstly, the data is put in a tabular formation. Organization makes it easier to draw inferences from the data.
It can be seen that 20 has the highest frequency of 4. Hence 20 is the mode since it occurs maximum number of times.
Median
Ø Median refers to the value which lies in the middle of the data when data is arranged in an increasing or decreasing order.
Ø Half of the observations lie above the median and the other half below it.
Ø To calculate the median, the data is first arranged in an ascending or descending order.
Ø Then the middle value is observed.
o For eg; 2, 4, 6, 8, 9
o 6 is the median in this case since it lies in the middle. There are two observations above and below 6.
Ø In case of odd number of observation, the value of median is one of the observations in the existing data.
Ø In case of odd number of observation, the value of median is one of the observations in the existing data.
Ø In case of even number of observations, the value of median is not one of the observations in the existing data.
o For eg : 2,4,6,8,9,10
o The median is the average of two middle numbers 6 and 8.
o Median = 6+8/2
o Median = 10/2 = 5
Problem
1. The scores in mathematics test (out of 25) of 15 students is as follows:
19, 25, 23, 20, 9, 20, 15, 10, 5, 16, 25, 20, 24, 12, 20
Find the mean of this data.
Solution:
The data is first arranged in an ascending order. We get :
5,9,10,12,15,16,19,20,20,20,20,23,24,25,25
It can be seen from this arrangement that 20 at the eight place is in the middle of the data. There are 7 observations below 20 and 7 observations above 20.
Therefore, 20 is the median of the data.
2. The weights (in kg.) of 15 students of a class are:
38, 42, 35, 37, 45, 50, 32, 43, 43, 40, 36, 38, 43, 38, 47

Find the mode and median of this data.
Solution:
Firstly, data will be arranged in an ascending order in a tabular format.
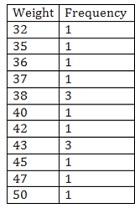
The observation with the highest frequency is the mode. 38kgs and 43kgs are the mode since the maximum numbers of students have these two weights. The frequency is maximum at these two observations, which is 3.
To find out the median, the data is first arranged in ascending order. Hence, the table has weights in ascending order.
(ii) Is there more than one mode?
There are two modes because two observations have highest and equal frequency. The two observations are 38 and 43.
Bar graph
Ø A bar graph is a representation of numbers using bars of uniform width and the lengths of the bars depend upon the frequency and the scale you have chosen.
Ø It is a method of representing data visually. In the case of bar graph or bar diagram, Bars of uniform width are drawn horizontally or vertically with equal spacing between them and then the length of each bar represents the given number.
Drawing a Bar Graph
Ø To draw a bar graph, first of all draw a horizontal line and a vertical line.
Ø On the horizontal line we will write the name of students and on vertical line we will write numerals which show what data is being represented.
Ø Same data can also be represented by interchanging the items on horizontal and vertical axis.
Ø It is important to take bars of same width keeping uniform gap between them. Next, a scale is chosen if needed.
Ø The scale varies according to the data given. One block is equivalent to ten units.
Example: Let there be 4 students A,B,C and D. The total marks Maths test is 40.Simple and double bar graphs can be obtained as:
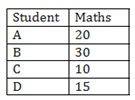
Ø First of all draw a horizontal line and a vertical line.
Ø On the horizontal line we will write the names of students and on vertical line we will write scores of maths.
Ø The scale taken is 1 unit = 5 marks.
Ø In simple bar graph only the score of one subject is marked.
Ø Same data can also be represented by interchanging the items on horizontal and vertical axis.
Ø The height of the bar represents the score of a student.
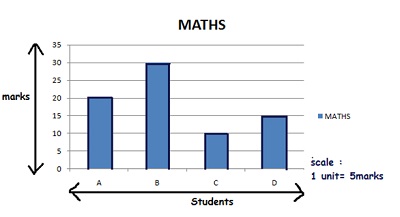
Simple Bar Graph (Only maths scores)
Double Bar Graph
Ø A simple bar graph represents one set of data. For e.g score of students in a Maths.
Ø A bar graph is drawn in a similar way to simple bar graph.
Ø A double graph represents two sets of data in one graph.For eg score of students in Maths and Hindi.
Example: Let there be 4 students A,B,C and D. The total marks for both hindi and Maths test is 40.Simple and double bar graphs can be obtained as:
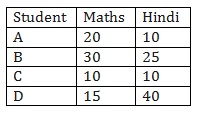
Ø First of all draw a horizontal line and a vertical line.
Ø On the horizontal line we will write the names of students and on vertical line we will write scores of maths and hindi.
Ø The scale taken is 1 unit = 5 marks.
Ø In a double bar graph both scores of both hindi and maths is marked. For e.g where Student is marked on Horizontal axis, two bars are drawn representing the bars of hindi and maths respectively. This is done for all the students.
Ø Same data can also be represented by interchanging the items on horizontal and vertical axis.
Ø The height of the bar represents the score of a student.
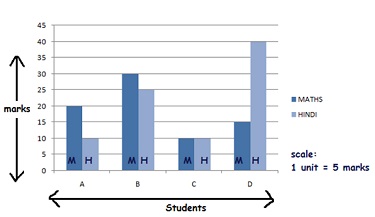
Double Bar Graph(
Both hindi and maths score)
Problem:
1. Read the bar graph and answer the questions that follow:
Number of books sold by a bookstore during five consecutive years.
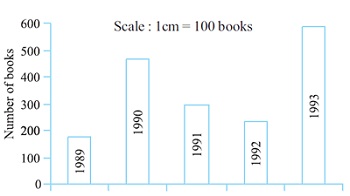
About how many books were sold in 1989? 1990? 1992?
The number of books sold in an year is depicted by the height of the bar. So, 175 books were sold in 1989. 475 books were sold in 1990.225books were sold in 1992.
In which year were about 475 books sold? About 225 books sold?
475 books were sold in the year 1990. 225books were sold in 1992.
In which years were fewer than 250 books sold?
The year with less than 250 books will have a shorter bar than the bar for the year 1992. Thus, 1989 is the year in which less than 250 books were sold.
Can you explain how you would estimate the number of books sold in 1989?
The height of the bar for the year 1989 is between 100 and 200. Between 100 and 200 there are ten units. The height is in the middle of 150 and 200.So, 175 books were sold in 1989.
2. The performance of students in 1st Term and 2nd Term is given. Draw a double bar graph choosing appropriate scale and answer the following:

Firstly, we take the subjects on horizontal axis and marks on the y axis.
The scale taken is 1unit = 10 marks.
The height of the bar represents the marks in a given test.
We get a double bar graph in which dark color represents term 1 and light color represents term 2.
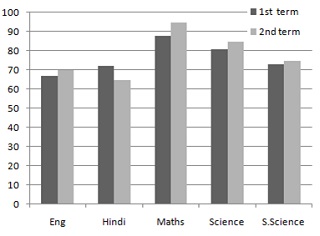
In which subject, has the child improved his performance the most?
The subject in which child has improved will have a taller term 2 bar than term1.The bar for the subject maths has the maximum difference between the height of the bars representing term 1 and term 2. Hence, the child has improved his performance in maths the most.
In which subject is the improvement the least?
The subject in which child has improved will have a term 2 bar that is marginally greater or equivalent to term1 bar. So, in social science the improvement is least.
Has the performance gone down in any subject?
The subject with a term 2 bar shorter than the term 1 bar is subject in which the student has gone down. Hence, the performance has gone down in Hindi.
Probability
Ø There are situations in our life, that are certain to happen, some that are impossible and some that may or may not happen.
Ø The situation that may or may not happen has a chance of happening.
Ø Probability is the chance of occurrence of an event.
Ø It tells us about the likelihood of the occurrence or non-occurrence of an event.
Ø Events that have many possibilities can have probability between 0 and 1.
Ø Those which have no chance of happening have probability 0 and those that are bound to happen have probability 1.

Probability
= ![]()
Problem
1. Tell whether the following is certain to happen, impossible, can happen but not certain.
You are older today than yesterday:
This event is certain to happen since we get older day by day.
A tossed coin will land heads up:
A coin has two sides- heads and tail. Since it possible to get either heads or tail, this event can happen.
A die when tossed shall land up with 8 on top:
A die only has 6 outcomes – 1, 2, 3, 4, 5 and 6. Since 8 is not there it is impossible to get 8 when a die is tossed.
2. There are 6 marbles in a box with numbers from 1 to 6 marked on each of them.
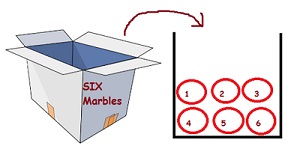
What is the probability of drawing a marble with number 2?
Total number of events = 6
Favorable event is to get the marble with number 2 marked on it.
Number of favorable events = 1
Probability =
![]()
Probability = 1/6
What is the probability of drawing a marble with number 5?
Total number of events = 6
Favorable event is to get the marble with number 5 marked on it.
Number of favorable events = 1
Probability =
![]()
Probability = 1/6