Lines and Angles

Point

A point is a geometrical element which has no dimensions.

Line

A line is a straight path which has no endpoints.

Line Segment

A line segment is a straight path which has two endpoints.

Ray

A ray is a line which has one endpoint and endless from another side.

Angles

The corners made by the intersection of two lines or line segments are called Angles.

We write angle as ∠ABC in first figure and ∠XOY, ∠ZOW, ∠YOW and ∠XOZ are angles in the second figure.

Related Angles

1. Complementary Angles

If the sum of two angles is 90° then they are said to be complementary angles.

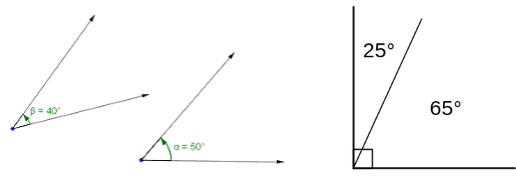
Or you can say that two angles which make up a right angle are called Complementary Angle.

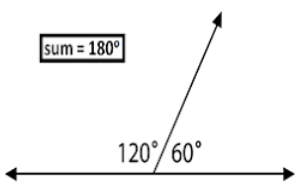
2. Supplementary Angles

If the sum of two angles is 180° then they are said to be supplementary angles. If two angles are supplementary then they are the supplement to each other.

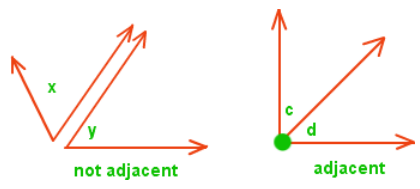
3. Adjacent Angles

It is the pair of two angles which are placed next to each other.

Adjacent angles have-

· A common vertex.

· A common arm.

· A non-common arm could be on either side of the common arm.

4. Linear Pair

A pair of adjacent angles whose non-common arm makes a single line i.e. they are the opposite rays.

A linear pair is also a pair of supplementary angles as their sum is 180°.

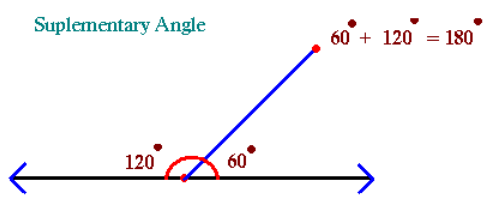
The above pair of angles is –

· Adjacent, as they have one common arm.

· Supplementary, as the sum of two angles, is 180°.

· The linear pair, as the sum is 180° and the non – common arms are opposite rays.

5. Vertically Opposite Angles

When two lines intersect each other then they form four angles. So that

· ∠a and ∠b is pair of vertically opposite angles.

· ∠n and ∠m is pair of vertically opposite angles.

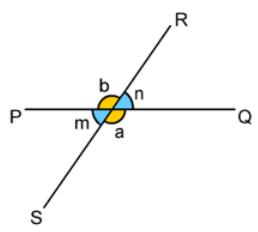
Vertically opposite angles are equal.

Pairs of Lines

1. Intersecting Lines

If two lines touch each other in such a way that there is a point in common then these lines are called intersecting lines.

That common point is called a Point of Intersection.

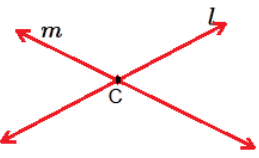
Here, line l and m intersect each other at point C.

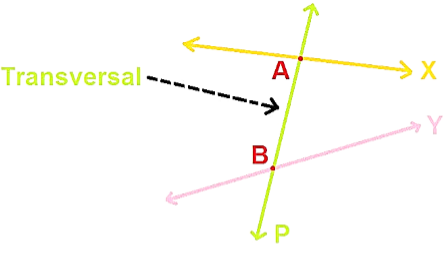
2. Transversal

If a line intersects two or more lines at different points then that line is called Transversal Line.

3. Angles made by a transversal

When a transversal intersects two lines then they make 8 angles.

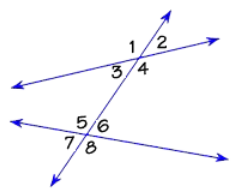
Some of the angles made by transversal-

Types of Angles	Angles shown in figure
Interior Angles	∠6, ∠5, ∠4, ∠3
Exterior Angles	∠7,∠8,∠1,∠2
Pairs of Corresponding Angles	∠1 and ∠5,∠2 and ∠6, ∠3 and ∠7,∠4 and ∠8
Pairs of Alternate Interior Angles	∠3 and ∠6,∠4 and ∠5
Pairs of Alternate Exterior Angles	∠1 and ∠8,∠2 and ∠7
Pairs of Interior Angles on the same side of the transversal	∠3 and ∠5,∠4 and ∠6

Transversal of Parallel Lines

The two lines which never meet with each other are called Parallel Lines. If we have a transversal on two parallel lines then-

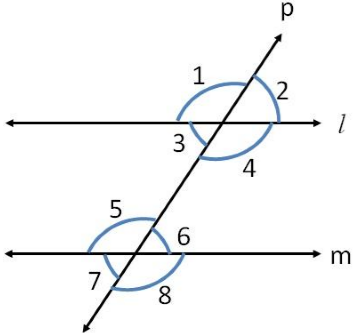
a. All the pairs of corresponding angles are equal.

∠3 = ∠7

∠4 = ∠8

∠1 = ∠5

∠2 = ∠6

b. All the pairs of alternate interior angles are equal.

∠3 = ∠6

∠4 = ∠5

c. The two Interior angles which are on the same side of the transversal will always be supplementary.

∠3 + ∠5 = 180°

∠4 + ∠6 = 180°

Checking for Parallel Lines

This is the inverse of the above properties of the transversal of parallel lines.

· If a transversal passes through two lines so that the pairs of corresponding angles are equal, then these two lines must be parallel.

· If a transversal passes through two lines in so that the pairs of alternate interior angles are equal, then these two lines must be parallel.

· If a transversal passes through two lines so that the pairs of interior angles on the same side of the transversal are supplementary, then these two lines must be parallel.