Perimeter and Area

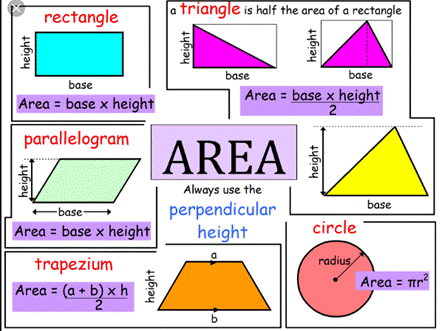
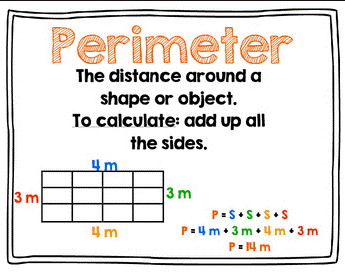
· Perimeter is the distance around a closed figure while area is the part of plane or region occupied by the closed figure.

· Perimeter of a regular polygon = number of sides × length of one side

· Perimeter of a square = 4 × side

· Perimeter of a rectangle = 2 × (l + b) Area of a rectangle = l × b,

· Area of a square = side × side

Example 1 A door-frame of dimensions 3 m × 2 m is fixed on the wall of dimension 10 m × 10 m. Find the total labour charges for painting the wall if the labour charges for painting 1 m2 of the wall is 2.50.

Solution

Painting of the wall has to be done excluding the area of the door.

Area of the door = l × b = 3 × 2 m = 6 m

Area of wall including door = side × side = 10 m × 10 m = 100 m

Area of wall excluding door = (100 − 6) m = 94 m

Total labour charges for painting the wall = 2.50 × 94 = 235

Example 2 The area of a rectangular sheet is 500 cm. If the length of the sheet is 25 cm, what is its width? Also find the perimeter of the rectangular sheet.

Solution

Area of the rectangular sheet = 500 cm

Length (l) = 25 cm

Area of the rectangle = l × b (where b = width of the sheet)

Therefore, width b = Area/l = 500/ 25 = 20 cm

Perimeter of sheet = 2 × (l + b) = 2 × (25 + 20) cm = 90 cm

So, the width of the rectangular sheet is 20 cm and its perimeter is 90 cm.

Example 3 Anu wants to fence the garden in front of her house (Fig 11.5), on three sides with lengths 20 m, 12 m and 12 m. Find the cost of fencing at the rate of Rs.150 per metre.

Solution

The length of the fence required is the perimeter of the garden (excluding one side) which is equal to 20 m + 12 m + 12 m, i.e., 44 m.

Cost of fencing = Rs. 150 × 44 =Rs. 6,600.

Example 4 A wire is in the shape of a square of side 10 cm. If the wire is rebent into a rectangle of length 12 cm, find its breadth. Which encloses more area, the square or the rectangle?

Solution

Side of the square = 10 cm

Length of the wire = Perimeter of the square = 4 × side = 4 × 10 cm = 40 cm

Length of the rectangle, l = 12 cm.

Let b be the breadth of the rectangle.

Perimeter of rectangle = Length of wire = 40 cm

Perimeter of the rectangle = 2 (l + b)

Thus, 40 = 2 (12 + b) or 40/ 2 = 12 + b

Therefore, b = 20 − 12 = 8 cm

The breadth of the rectangle is 8 cm.

Area of the square = (side) 2 = 10 cm × 10 cm = 100 cm

Area of the rectangle = l × b = 12 cm × 8 cm = 96 cm

So, the square encloses more area even though its perimeter is the same as that of the rectangle.

Example 5 The area of a square and a rectangle are equal. If the side of the square is 40 cm and the breadth of the rectangle is 25 cm, find the length of the rectangle. Also, find the perimeter of the rectangle.

Solution

Area of square = (side) = 40 cm × 40 cm = 1600 cm

It is given that,

The area of the rectangle = The area of the square

Area of the rectangle = 1600 cm ,

Breadth of the rectangle = 25 cm.

Area of the rectangle = l × b

1600 = l × 25

1600 /25 = l or l = 64 cm

So, the length of rectangle is 64 cm.

Perimeter of the rectangle = 2 (l + b) = 2 (64 + 25) cm = 2 × 89 cm = 178 cm

So, the perimeter of the rectangle is 178 cm even though its area is the same as that of the square.

11.2.1 Triangles as Parts of Rectangles

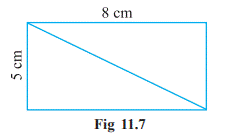
What is the area of each of these triangles?

You will find that sum of the areas of the two triangles is the same as the area of the rectangle. Both the triangles are equal in area.

The area of each triangle = ½(Area of the rectangle)

= ½ (lb)

= ½(85)

=40/2

= 20 cm

Take a square of side 5 cm and divide it into 4 triangles as shown Are the four triangles equal in area? Are they congruent to each other? (Superpose the triangles to check). What is the area of each triangle?

The area of each triangle = ¼(Area of the square)

= ¼(side

= 6.25 cm

11.2.2 Generalizing For Other Congruent Parts of Rectangles

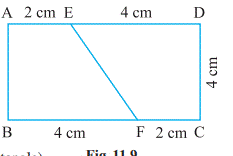
A rectangle of length 6 cm and breadth 4 cm is divided into two parts as shown in the Trace the rectangle on another paper and cut off the rectangle along EF to divide it into two parts. Superpose one part on the other, see if they match. (You may have to rotate them). Are they congurent? The two parts are congruent to each other.

So, the area of one part is equal to the area of the other part.

Therefore, the area of each congruent part = ½(The area of the rectangle)

= ½() cm

= 12 cm

11.3 Area of a Parallelogram

Can a parallelogram be converted into a rectangle of equal area? Draw a parallelogram on a graph paper as shown in Fig 11.10(i). Cut out the parallelogram. Draw a line from one vertex of the parallelogram perpendicular to the opposite side [Fig 11.10(ii)]. Cut out the triangle. Move the triangle to the other side of the parallelogram.

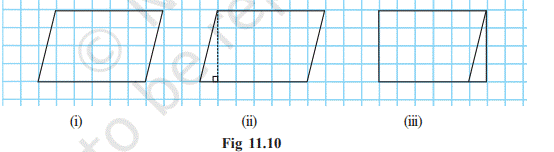
What shape do you get? You get a rectangle. Is the area of the parallelogram equal to the area of the rectangle formed? Yes, area of the parallelogram = area of the rectangle formed what are the length and the breadth of the rectangle? We find that the length of the rectangle formed is equal to the base of the parallelogram and the breadth of the rectangle is equal to the height of the parallelogram

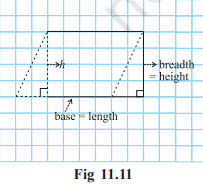
Now, Area of parallelogram = Area of rectangle = length × breadth = l × b

But the length l and breadth b of the rectangle are exactly the base b and the height h, respectively of the parallelogram.

Thus, the area of parallelogram = base × height = b × h.

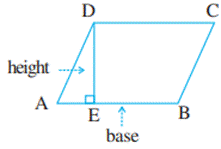
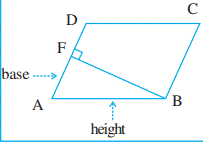
Any side of a parallelogram can be chosen as base of the parallelogram. The perpendicular dropped on that side from the opposite vertex is known as height (altitude). In the parallelogram ABCD, DE is perpendicular to AB. Here AB is the base and DE is the height of the parallelogram. In this parallelogram ABCD, BF is the perpendicular to opposite side AD. Here AD is the base and BF is the height.

11.4 Area Of A Triangle

Area of each triangle = ½(Area of parallelogram)

= ½(base × height) (Since area of a parallelogram

= (base × height) = ½(bh) (or 1/2 bh, in short)

All the congruent triangles are equal in area but the triangles equal in area need not be congruent.

Example 6 One of the sides and the corresponding height of a parallelogram are 4 cm and 3 cm respectively. Find the area of the parallelogram

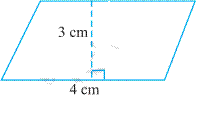
Solution

Given that length of base (b) = 4 cm, height (h) = 3 cm

Area of the parallelogram = b × h = 4 cm × 3 cm = 12 cm

Example 7 Find the height ‘x’ if the area of the parallelogram is 24 cm and the base is 4 cm.

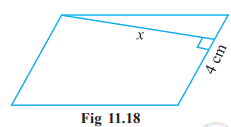
Solution

Area of parallelogram = b × h

Therefore, 24 = 4 × x (Fig 11.18) or 24/ 4 = x or x = 6 cm

So, the height of the parallelogram is 6 cm.

Example 8 The two sides of the parallelogram ABCD are 6 cm and 4 cm. The height corresponding to the base CD is 3 cm (Fig 11.19). Find the

(i) Area of the parallelogram. (ii) The height corresponding to the base AD.

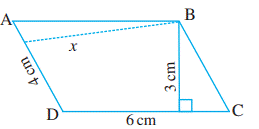
Solution

(i) Area of parallelogram = b × h = 6 cm × 3 cm = 18 cm

(ii) Base (b) = 4 cm, height = x (say),

Area = 18 cm

Area of parallelogram = b × x

18 = 4 × x

18/4 = x

Therefore, x = 4.5 cm

Thus, the height corresponding to base AD is 4.5 cm.

Example 9 Find the area of the following triangles (Fig 11.20).

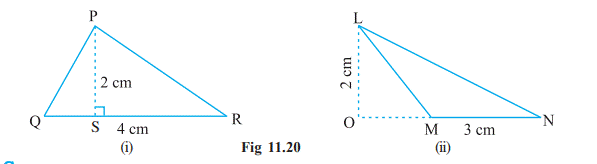
Solution

(i) Area of triangle = 1/2 bh

= 1 /2 × QR × PS

= 1/2 × 42 cm

= 4 cm

(ii) Area of triangle = 1/2 bh

= 1/ 2 × MN × LO

= 1/ 2 ×3 × 2 cm = 3 cm

11.5 Circles

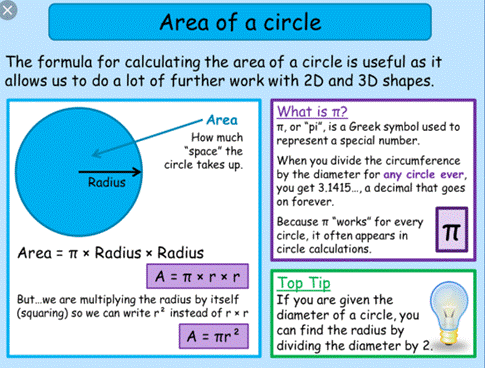
11.5.1 Circumference of A Circle

The distance around a circular region is known as its circumference.

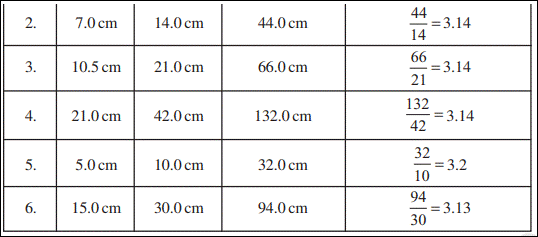
What do you infer from the above table? Is this ratio approximately the same? Yes.

Can you say that the circumference of a circle is always more than three times its diameter? Yes.

This ratio is a constant and is denoted by π (pi).

Its approximate value is 22/ 7 or 3.14.

So, we can say that C/ d = π,

Where ‘C’ represents circumference of the circle and‘d’ its diameter.

Or
C = πd we know that diameter (d) of a circle is twice the radius (r)

i.e., d = 2r So, C = πd = π × 2r or C = 2πr.

Example 12 What is the circumference of a circle of diameter 10cm (Take π = 3.14)?

Solution

Diameter of the circle (d) = 10 cm

Circumference of circle = πd = 3.14 × 10 cm = 31.4 cm

So, the circumference of the circle of diameter 10 cm is 31.4 cm.

Example 13 What is the circumference of a circular disc of radius 14 cm? Use π = 22/ 7

Solution

Radius of circular disc (r) = 14 cm

Circumference of disc = 2πr = 2 22 /7 × 14 cm = 88 cm

So, the circumference of the circular disc is 88 cm.

Example 14 The radius of a circular pipe is 10 cm. What length of a tape is required to wrap once around the pipe (π = 3.14)?

Solution

Radius of the pipe (r) = 10 cm

Length of tape required is equal to the circumference of the pipe.

Circumference of the pipe = 2πr = 2 × 3.14 × 10 cm = 62.8 cm

Therefore, length of the tape needed to wrap once around the pipe is 62.8 cm.

Example 15 Find the perimeter of the given shape (Fig 11.32) (Take π = 22 7).

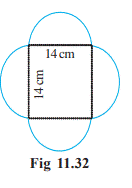
Solution

In this shape we need to find the circumference of semicircles on each side of the square.

Do you need to find the perimeter of the square also? No.

The outer boundary, of this figure is made up of semicircles.

Diameter of each semicircle is 14 cm.

We know that:

Circumference of the circle = πd

Circumference of the semicircle = 1/2 πd = ½ 22 / 7 × 14 cm = 22 cm

Circumference of each of the semicircles is 22 cm

Therefore, perimeter of the given figure = 4 × 22 cm = 88 cm

11.5.2 Area of Circle

Area of the circle = Area of rectangle thus formed = l × b

= (Half of circumference) × radius

= (1/2 2× π) × r = πr

So, the area of the circle = πr

Example 17 Find the area of a circle of radius 30 cm (use π = 3.14).

Solution

Radius, r = 30 cm

Area of the circle = πr = 3.14 × = 2,826 cm

Example 18 Diameter of a circular garden is 9.8 m. Find its area.

Solution

Diameter, d = 9.8 m.

Therefore, radius r = 9.8 ÷ 2 = 4.9 m

Area of the circle = πr = 22/7 × (4.9 m = 22/ 7 × 4.9 4.9 ... m = 75.46 m

Example 19 The adjoining figure shows two circles with the same centre. The radius of the larger circle is 10 cm and the radius of the smaller circle is 4 cm.

Find: (a) the area of the larger circle (b) the area of the smaller circle (c) the shaded area between the two circles. (π = 3.14)

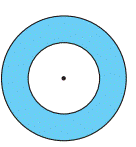
Solution

(a) Radius of the larger circle = 10 cm

So, area of the larger circle = πr = 3.14 × 10 × 10 = 314 cm

(b) Radius of the smaller circle = 4 cm

Area of the smaller circle = πr = 3.14 × 4 × 4 = 50.24 cm

11.6 Conversion of Units

We know that 1 cm = 10 mm. Can you tell 1 cmis equal to how many mm?

Let us explore similar questions and find how to convert units while measuring areas to another unit.

Draw a square of side 1cm (Fig 11.38), on a graph sheet.

You find that this square of side 1 cm will be divided into 100 squares, each of side 1 mm. Area of a square of side 1cm = Area of 100 squares, of each side 1mm.

Therefore, 1 cm = 100 × 1 mm or 1 cm = 100 mm

Similarly, 1 m = 1 m × 1 m = 100 cm × 100 cm (As 1 m = 100 cm) = 10000 cm

Now can you convert 1 kminto m?

In the metric system, areas of land are also measured in hectares [written “ha” in short].

A square of side 100 m has an area of 1 hectare.

So, 1 hectare = 100 × 100 m = 10,000 m

When we convert a unit of area to a smaller unit, the resulting number of units will be bigger. For example,

1000 cm = 1000 × 100 mm = 100000 mm

But when we convert a unit of area to a larger unit, the number of larger units will be smaller. For example, 1000 cm = 1000/10000 m = 0.1 m

11.7 Applications

You must have observed that quite often, in gardens or parks, some space is left all around in the form of path or in between as cross paths. A framed picture has some space left all around it. We need to find the areas of such pathways or borders when we want to find the cost of making them.

Example 20 A rectangular park is 45 m long and 30 m wide. A path 2.5 m wide is constructed outside the park. Find the area of the path.

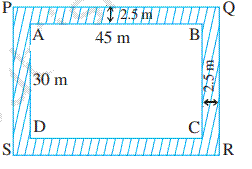
Solution

Let ABCD represent the rectangular park and the shaded region represent the path 2.5 m wide.

To find the area of the path, we need to find (Area of rectangle PQRS – Area of rectangle ABCD).

We have,

PQ = (45 + 2.5 + 2.5) m

= 50 m PS = (30 + 2.5 + 2.5) m

= 35 m

Area of the rectangle ABCD = l × b = 45 × 30 m = 1350 m

Area of the rectangle PQRS = l × b = 50 × 35 m = 1750 m

Area of the path = Area of the rectangle PQRS − Area of the rectangle ABCD

= (1750 − 1350) m

= 400 m

Example 21 A path 5 m wide runs along inside a square park of side 100 m. Find the area of the path. Also find the cost of cementing it at the rate of Rs.250 per 10 m .

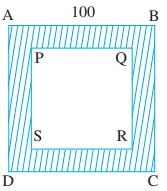
Solution

Let ABCD be the square park of side 100 m.

The shaded region represents the path 5 m wide.

PQ = 100 – (5 + 5) = 90 m

Area of square ABCD = (side = (100 m = 10000 m

Area of square PQRS = (side = (90 m = 8100 m

Therefore, area of the path = (10000 − 8100) m = 1900 m

Cost of cementing 10 m =Rs.250

Therefore, cost of cementing 1 m =250/ 10

So, cost of cementing 1900 m = Rs. 250 /10 ×1900 =Rs. 47,500

Example 22 Two cross roads, each of width 5 m, run at right angles through the centre of a rectangular park of length 70 m and breadth 45 m and parallel to its sides. Find the area of the roads. Also find the cost of constructing the roads at the rate of 105 per m .

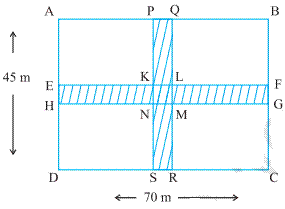
Solution

Area of the cross roads is the area of shaded portion, i.e., the area of the rectangle PQRS and the area of the rectangle EFGH.

But while doing this, the area of the square KLMN is taken twice, which is to be subtracted. Now, PQ = 5 m and PS = 45 m

EH = 5 m and EF = 70 m

KL = 5 m and KN = 5 m

Area of the path = Area of the rectangle PQRS + area of the rectangle EFGH – Area of the square KLMN

= PS × PQ + EF × EH – KL × KN

= (45 × 5 + 70 × 5 − 5 × 5) m

= (225 + 350 − 25) m2 = 550 m

Cost of constructing the path =Rs. 105 × 550 = Rs. 57,750