Symmetry

If two or more parts of a figure are identical after folding or flipping then it is said to be symmetry. To be symmetrical the two halves of a shape must be of same shape and size.

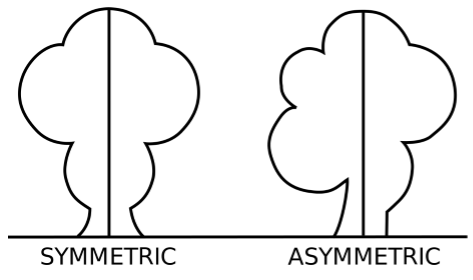
If the shape is not symmetrical then it is said to be asymmetrical.

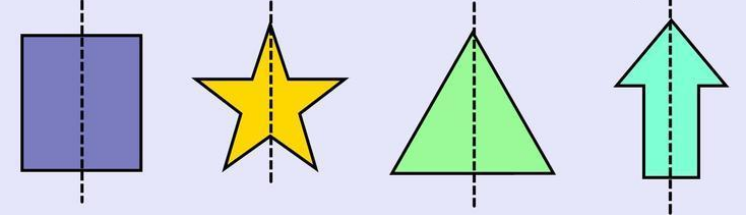
Line of Symmetry

It is an imaginary line which divides the image into two equal halves. It could be horizontal, vertical or diagonal. There could be one or more than one line of symmetry in a figure.

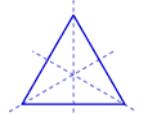
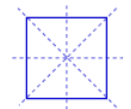
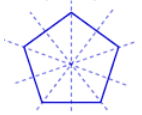
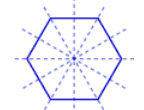
Lines of Symmetry for Regular Polygons

If all the sides and angles of a polygon are equal then it is said to be a regular polygon. Like the equilateral triangle, square etc.

All the regular polygons are symmetrical shapes.

In the regular polygon, the number of lines of symmetry is the same as the number of its sides.

Regular Polygon	Number of Sides	Line of Symmetry	Image
Equilateral Triangle	3	3
Square	4	4
Regular Pentagon	5	5
Regular Hexagon	6	6

Types of Symmetry

There are two types of Symmetry

1. Reflection Symmetry

If we draw a dotted line which gives the mirror reflection of the other half of the image then it is reflection symmetry. It is the same as basic symmetry which tells us that if the dotted line divides the image into two equal halves then it is the reflective symmetry of the figure.

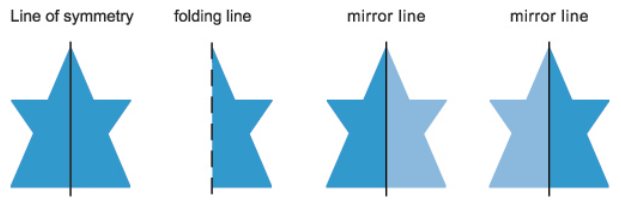
2. Rotational Symmetry

If we rotate the image at a centre point of the image at 360° then the number of times the image looks the same, shows the rotational symmetry of the image.

Rotational Symmetry

· If a figure rotates at a fixed point then that point is the centre of Rotation.

· It could rotate clockwise or anticlockwise.

· While rotation the measurement of the angle which we take is the angle of rotation. And a complete rotation is of 360°.

· If the angle of rotation is 180° then it is called Half Turn and if the angle of rotation is 90° then it is called a Quarter Turn.

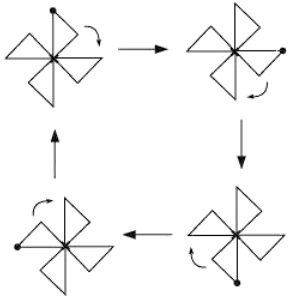
This image looks symmetrical but there is no line of symmetry in it i.e. there is any such line which divides it into two equal halves. But if we rotate it at 90° about its centre then it will look exactly the same. This shows that it has Rotational Symmetry.

While rotating, there are four positions when the image looks exactly the same. So this windmill has a rotational symmetry of order 4 about its centre.

Example

What is the Rotational symmetry of the given figure?

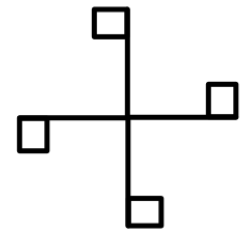
Solution:

To find the rotational symmetry, we have to find

· The angle of rotation = 90°

· Direction = clockwise

· Order of rotation = 4

This shows that if the given figure rotates anticlockwise at 90° around its centre then it has rotational symmetry of order 4.

Line Symmetry and Rotational Symmetry

Some shapes have only line symmetry and some shapes have only rotational symmetry but there are some shapes which have both types of symmetry.

Example

Find whether the given image has rotational symmetry or line symmetry or both.

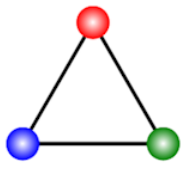
Solution:

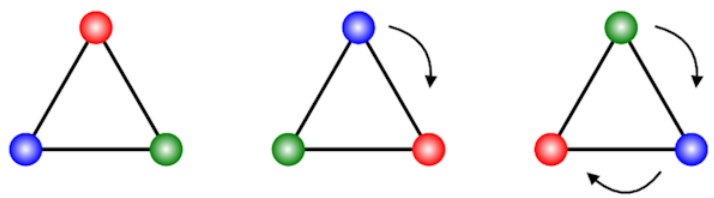
Rotational Symmetry

If we rotate the image clockwise at an angle of 360° around its centre then it will have rotational symmetry of order 1 or no symmetry as every image will look same if we rotate it at 360°.

This will not look the same at every 120° because of the colour of the balls at its edges.

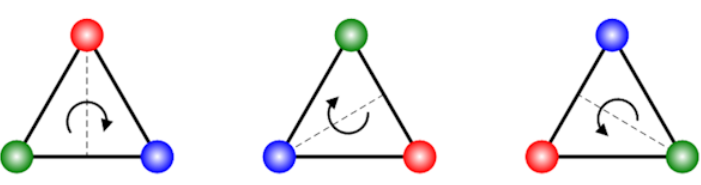
Line Symmetry

This figure will have three line of symmetry. As there are three possible lines which can divide the image into two equal halves. 

Example

Tell whether the figures below have line symmetry or rotational symmetry or both.

Solution:

· The first figure have 2 line of symmetry and rotational symmetry of order 2.

· The second figure has no line of symmetry but have rotational symmetry of order 3.

· The third figure has 1 line of symmetry but no rotational symmetry.

· The fourth figure has 1 line of symmetry but no rotational symmetry.