Visualizing Solid Shapes

15.1 Introduction: Plane Figures and Solid Shapes

In our day to day life, we see several objects like books, balls, ice-cream cones etc., around us which have different shapes. One thing common about most of these objects is that they all have some length, breadth and height or depth. That is, they all occupy space and have three dimensions. Hence, they are called three dimensional shapes.

15.2 Faces, Edges And Vertices

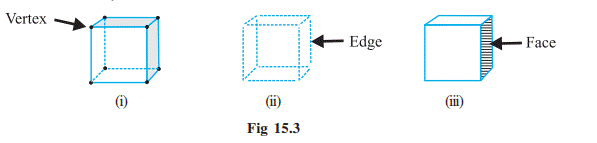
The 8 corners of the cube are its vertices. The 12 line segments that form the skeleton of the cube are its edges. The 6 flat square surfaces that are the skin of the cube are its faces.

15.3 Nets For Building 3-D Shapes

Take a cardboard box. Cut the edges to lay the box flat. You have now a net for that box. A net is a sort of skeleton-outline in 2-D [Fig154 (i)], which, when folded [Fig154 (ii)], results in a 3-D shape [Fig154 (iii)].

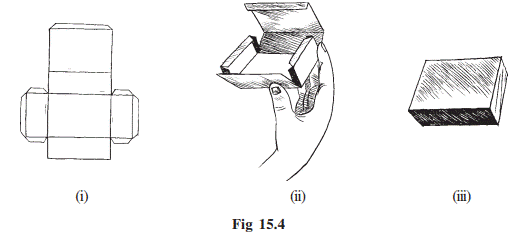
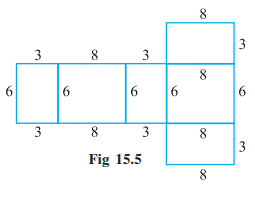
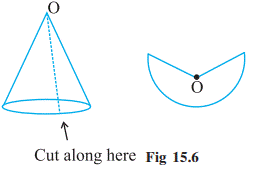
Here you got a net by suitably separating the edges. Is the reverse process possible? Here is a net pattern for a box (Fig 15.5). Copy an enlarged version of the net and try to make the box by suitably folding and gluing together. (You may use suitable units). The box is a solid. It is a 3-D object with the shape of a cuboid. Similarly, you can get a net for a cone by cutting a slit along its slant surface.

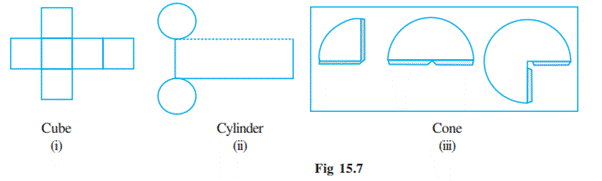
You have different nets for different shapes. Copy enlarged versions of the nets given (Fig 15.7) and try to make the 3-D shapes indicated. (You may also like to prepare skeleton models using strips of cardboard fastened with paper clips).

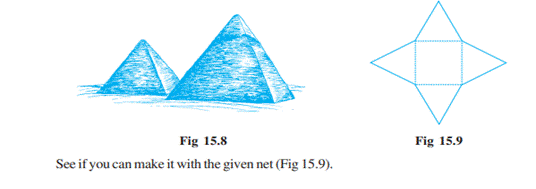
We could also try to make a net for making a pyramid like the Great Pyramid in Giza (Egypt) (Fig 15.8). That pyramid has a square base and triangles on the four sides.

15.4 Drawing Solids on A Flat Surface

Your drawing surface is paper, which is flat. When you draw a solid shape, the images are somewhat distorted to make them appear three-dimensional. It is a visual illusion. You will find here two techniques to help you.

15.4.1 Oblique Sketches

Here is a picture of a cube (Fig 15.11). It gives a clear idea of how the cube looks like, when seen from the front. You do not see certain faces. In the drawn picture, the lengths are not equal, as they should be in a cube. Still, you are able to recognize it as a cube. Such a sketch of a solid is called an oblique sketch. How can you draw such sketches?

Let us attempt to learn the technique. You need a squared (lines or dots) paper.

Initially practicing to draw on these sheets will later make it easy to sketch them on a plain sheet (without the aid of squared lines or dots!)

Let us attempt to draw an oblique sketch of a 3 × 3 × 3 (each edge is 3 units) cube (Fig 15.12).

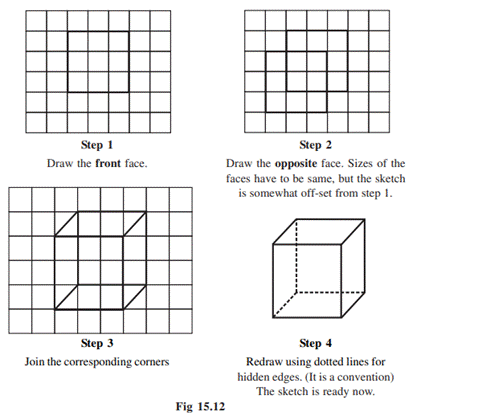
In the oblique sketch above, did you note the following?

(i) The sizes of the front faces and its opposite are same; and

(ii) The edges, which are all equal in a cube, appear so in the sketch, though the actual measures of edges are not taken so.

You could now try to make an oblique sketch of a cuboid (remember the faces in this case are rectangles)

Note:

You can draw sketches in which measurements also agree with those of a given solid. To do this we need what is known as an isometric sheet. Let us try to make a cuboid with dimensions 4 cm length, 3 cm breadth and 3 cm height on given isometric sheet.

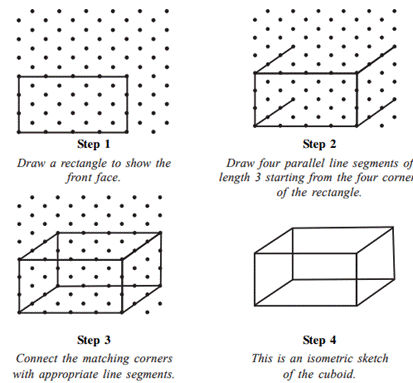
15.4.2 Isometric Sketches

Have you seen an isometric dot sheet? (A sample is given at the end of the book). Such a sheet divides the paper into small equilateral triangles made up of dots or lines. To draw sketches in which measurements also agree with those of the solid, we can use isometric dot sheets. [Given on inside of the back cover (3rd cover page).]

Let us attempt to draw an isometric sketch of a cuboid of dimensions 4 × 3 × 3 (which means the edges forming length, breadth and height are 4, 3, 3 units respectively)

Example 1 Here is an oblique sketch of a cuboid [Fig 15.14(i)]. Draw an isometric sketch that matches this drawing.

Solution

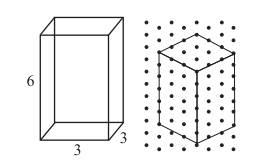
Here is the solution [Fig 15.14(ii)]. Note how the measurements are taken care of.

15.4.3 Visualizing Solid Objects

Here are some activities you could try in your free time to help you visualize some solid objects and how they look. Take some cubes and arrange them.

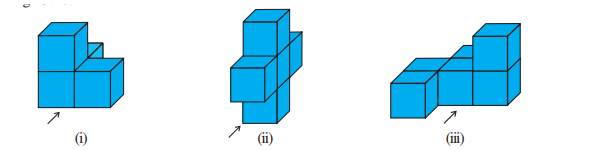
Now ask your friend to guess how many cubes there are when observed from the view shown by the arrow mark.

Example 2 If two cubes of dimensions 2 cm by 2cm by 2cm are placed side by side, what would the dimensions of the resulting cuboid be?

Solution

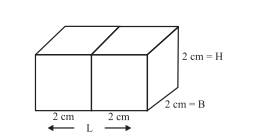
As you can see (Fig 15.18) when kept side by side, the length is the only measurement which increases, it becomes 2 + 2 = 4 cm. The breadth = 2 cm and the height = 2 cm.

15.5 Viewing Different Sections of a Solid

Now let us see how an object which is in 3-D can be viewed in different ways.

15.5.1 One Way to View an Object is by Cutting or Slicing

Slicing game

Here is a loaf of bread (Fig 15.20). It is like a cuboid with a square face. You ‘slice’ it with a knife. When you give a ‘vertical’ cut, you get several pieces, as shown in the Figure 15.20. Each face of the piece is a square! We call this face a ‘cross-section’ of the whole bread. The cross section is nearly a square in this case.

Beware! If your cut is not ‘vertical’ you may get a different cross section! Think about it. The boundary of the cross-section you obtain is a plane curve. Do you notice it?

A kitchen play

Have you noticed cross-sections of some vegetables when they are cut for the purposes of cooking in the kitchen? Observe the various slices and get aware of the shapes that result as cross-sections.

Play this

Make clay (or plastic) models of the following solids and make vertical or horizontal cuts. Draw rough sketches of the cross-sections you obtain. Name them wherever you can.

15.5.2 Another Way is by Shadow Play

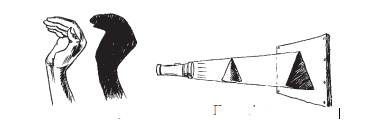
A shadow play

Shadows are a good way to illustrate how three-dimensional objects can be viewed in two dimensions. Have you seen a shadow play? It is a form of entertainment using solid articulated figures in front of an illuminated back-drop to create the illusion of moving images. It makes some indirect use of ideas in Mathematics.

You will need a source of light and a few solid shapes for this activity. (If you have an overhead projector, place the solid under the lamp and do these investigations.)

Keep a torchlight, right in front of a Cone. What type of shadow does it cast on the screen?

The solid is three-dimensional; what is the dimension of the shadow?

If, instead of a cone, you place a cube in the above game, what type of shadow will you get? Experiment with different positions of the source of light and with different positions of the solid object. Study their effects on the shapes and sizes of the shadows you get.

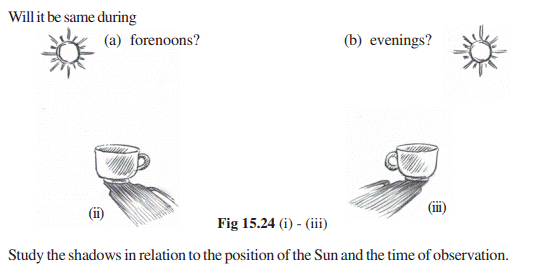
Here is another funny experiment that you might have tried already: Place a circular plate in the open when the Sun at the noon time is just right above. What is the shadow that you obtain?

15.5.3 A Third Way is by Looking at it from Certain Angles to Get Different Views

One can look at an object standing in front of it or by the side of it or from above. Each time one will get a different view.

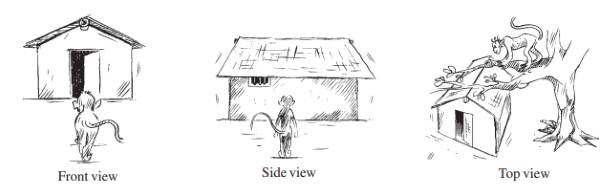
Here is an example of how one gets different views of a given building

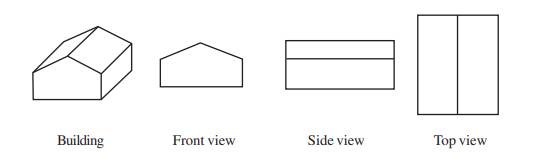
You could do this for figures made by joining cubes.

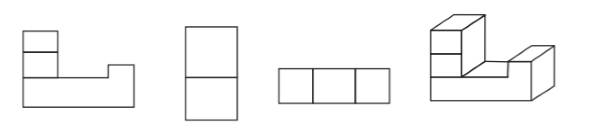
Try putting cubes together and then making such sketches from different sides.